
- •Абсолютная и условная сходимость числовых рядов. Свойства абсолютно сходящихся рядов.
- •Функциональные ряды. Точка сходимости ряда. Степенной ряд.
- •Мажорируемые и равномерно сходящиеся ряды.
- •Сходимость степенных рядов. Теорема Абеля. Радиус сходимости степенного ряда.
- •Определение радиуса сходимости степенного ряда. Признак Даламбера. Радикальный признак Коши. Свойства степенных рядов.
- •Ряды Тейлора и Маклорена. Примеры (разложение в ряд Тейлора элементарных функций).
- •Метрическое пространство. Фундаментальная последовательность. Полное метрическое пространство.
- •Линейное пространство. Аксиомы линейного пространства. Нормированное пространство. Банаховы пространства.
- •Ряды Фурье. Разложение функции по произвольной ортогональной системе функций.
- •Тригонометрические ряды Фурье. Разложение в ряд Фурье четных и нечетных функций.
- •Комплексные числа и действия над ними.
- •Возведение в степень
- •Последовательности комплексных чисел. Сходимость последовательности комплексных чисел.
- •Функции комплексных переменных. Основные элементарные функции комплексного переменного.
- •Производная функции комплексного переменного. Условия Даламбера-Эйлера. Определение аналитической функции. Дифференциал. Производная элементарной функции.
- •Интегрирование функции комплексного переменного. Сведение интеграла к сумме криволинейных интегралов второго рода.
- •Теорема Коши. Первообразная и неопределенный интеграл. Формула Ньютона-Лейбница.
- •Интегральная формула Коши. Ряды Тейлора и Лорана. Физический смысл аналитической функции.
- •Классификация особых точек аналитической функции. Вычисление вычета в полюсе. Теорема о вычетах.
- •Обыкновенные дифференциальные уравнения.
- •Закон радиоактивного распада.
- •Общий интеграл. Общее решение. Задача Коши. Теорема Коши о существовании и единственности решения.
- •Решение дифференциальных уравнений с разделяющимися переменными.
- •Метод вариации произвольной постоянной.
- •Уравнение в полных дифференциалах.
- •Дифференциальные уравнения высших порядков. Уравнения, допускающие понижение порядка.
- •Линейные дифференциальные уравнения. Определитель Вронского. Фундаментальная система решений.
- •Линейные однородные дифференциальные уравнения n-того порядка. Фундаментальная система решений. Определитель Вронского.
- •Интегрирование линейных однородных дифференциальных уравнений второго порядка.
- •Решение линейных неоднородных дифференциальных уравнений со специальной правой частью.
- •Системы дифференциальных уравнений, разрешенных относительно производных. Теорема Коши. Метод исключения для решения систем дифференциальных уравнений.
- •Случайные события и их вероятности.
- •Операции над событиями. Классическое определение вероятности. Геометрическое определение вероятности.
- •Свойства вероятности. Применение комбинаторики к вычислению вероятности.
- •Условные вероятности. Независимость событий.
- •Формула полной вероятности. Формула Байеса.
- •Предельная теорема в схеме Бернулли. Формула Пуассона.
- •Локальная и интегральная теоремы Муавра-Лапласа.
- •Системы случайных величин. Функции распределения системы случайных величин.
- •Плотности вероятности системы случайных величин. Условные законы распределения.
- •Математическое ожидание и дисперсия случайных величин.
- •Условное математическое ожидание. Корреляционный момент и коэффициент корреляции. Свойства коэффициента корреляции.
- •Сходимость по вероятности. Второе неравенство Чебышева.
- •Правило трех сигм. Теорема Маркова.
- •Теорема Чебышева. Закон больших чисел. Центральная предельная теорема (теорема Ляпунова).
- •Предмет математической статистики. Задачи математической статистики. Генеральная и выборочная совокупности.
- •Эмпирическая функция распределения. Числовые характеристики статистического распределения.
- •Статистическая оценка параметров. Несмещенная, эффективная и состоятельная оценки.
- •Теорема о выборочном среднем. Исправленная выборочная дисперсия.
- •Метод моментов. Метод максимального правдоподобия.
- •Интервальное оценивание параметров. Доверительный интервал для математического ожидания при известной дисперсии.
- •Доверительный интервал для математического ожидания нормального распределения при известной дисперсии.
- •Доверительный интервал для математического ожидания при неизвестной дисперсии.
- •Проверка статистических гипотез. Критерий Колмогорова.
Доверительный интервал для математического ожидания нормального распределения при известной дисперсии.
Пусть случайная величина (можно говорить о генеральной совокупности) распределена по нормальному закону, для которого известна дисперсия D = 2 ( > 0). Из генеральной совокупности (на множестве объектов которой определена случайная величина) делается выборка объема n. Выборка x1, x2,..., xn рассматривается как совокупность n независимых случайных величин, распределенных так же как (подход, которому дано объяснение выше по тексту).
Ранее также обсуждались и доказаны следующие равенства:
Mx1 = Mx2 = ... = Mxn = M;
Dx1 = Dx2 = ... = Dxn = D;
![]() M;
M;
![]() D
/n;
D
/n;
Достаточно
просто доказать (мы доказательство
опускаем), что случайная величина
![]() в данном случае также распределена по
нормальному закону.
в данном случае также распределена по
нормальному закону.
Обозначим неизвестную величину M через a и подберем по заданной надежности число d > 0 так, чтобы выполнялось условие:
P( – a < d) = (1)
Так как случайная величина распределена по нормальному закону с математическим ожиданием M = M = a и дисперсией D = D /n = 2/n, получаем:
P(
–
a
< d)
=P(a
– d <
< a
+ d)
= =

Осталось
подобрать d
таким, чтобы выполнялось равенство
![]() или
или
![]() .
.
Для любого [0;1] можно по таблице найти такое число t, что ( t )= / 2. Это число t иногда называют квантилем.
Теперь
из равенства
![]() определим
значение d:
определим
значение d:![]() .
.
Окончательный
результат получим, представив формулу
(1) в виде: ![]() .
.
Смысл
последней формулы состоит в следующем:
с надежностью
доверительный
интервал ![]()
покрывает
неизвестный параметр a
= M
генеральной
совокупности. Можно сказать иначе:
точечная оценка
определяет значение параметра
M
с точностью d=
t /![]() и
надежностью .
и
надежностью .
Задача. Пусть имеется генеральная совокупность с некоторой характеристикой, распределенной по нормальному закону с дисперсией, равной 6,25. Произведена выборка объема n = 27 и получено средневыборочное значение характеристики = 12. Найти доверительный интервал, покрывающий неизвестное математическое ожидание исследуемой характеристики генеральной совокупности с надежностью =0,99.
Решение.
Сначала по таблице для функции Лапласа
найдем значение t
из
равенства
(t)
=
/ 2
= 0,495.
По полученному значению
t
=
2,58 определим точность оценки (или
половину длины доверительного интервала)
d:
d
=
2,52,58 / ![]()
1,24. Отсюда получаем искомый доверительный
интервал: (10,76; 13,24).
1,24. Отсюда получаем искомый доверительный
интервал: (10,76; 13,24).
Доверительный интервал для математического ожидания при неизвестной дисперсии.
Пусть величина X определена
по нормальному закону распределения с
параметра
![]() и
и![]() ,
где
,
где
![]() ,
- среднеквадратичное отклонение.
Требуется найти
,
чтобы выполнялось
,
- среднеквадратичное отклонение.
Требуется найти
,
чтобы выполнялось
![]()
![]() - доверительная вероятность(надежность).
- доверительная вероятность(надежность).
Другими словами нам требуется найти
доверительный интервал
![]() при доверительной вероятности
при доверительной вероятности
![]() .
.
С вероятностью
величина
находиться в указанном интервале. Введем
случайную величину.
 - Стьюдент (Госеет). S –
исправленное выборочное отклонение по
случайной величине X.
Случайная величина D –
имеет распределение Стьюдента с n-1
степенью свободы.
- Стьюдент (Госеет). S –
исправленное выборочное отклонение по
случайной величине X.
Случайная величина D –
имеет распределение Стьюдента с n-1
степенью свободы.
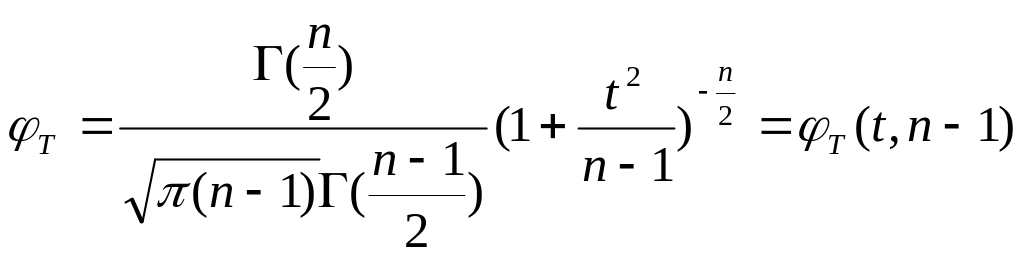 ,
где
,
где
![]() - гамма функция, в общем случае не берется,
но есть таблицы. Но при
- гамма функция, в общем случае не берется,
но есть таблицы. Но при
![]() берется
берется
![]()

![]()

![]()
 - трансцендентное уравнение для
определения
- трансцендентное уравнение для
определения
![]() по таблице. Чем ближе
к 1 тем шире интервал
.
по таблице. Чем ближе
к 1 тем шире интервал
.
