1:( N рез:60) – время за которое совершается 1оборот;

Таким образом, время прохождения звуковой волны от начала выхлопа до момента перекрытия выхлопного окна поршнем (обозначим как t^в) будет:

t^в = Ф_вых * [1:( n _рез:60)]:360 c.

Достаточно умножить результат на скорость волны в среде выхлопных газов и поделить на 2 (весь путь до отражателя и назад) – получим ИСКОМУЮ длину ГДН .

- 14 –

.

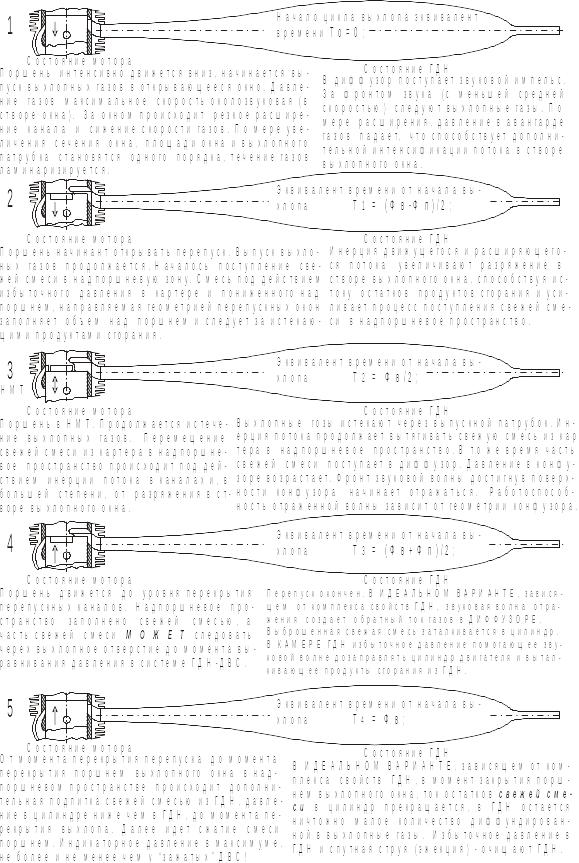
Рис. 10 Процессы протекающие в ГДН в ДВС при их полной синхронизации.

Фраза (см.положение 5) - «Индикаторное давление не более и не менее чем у «зажатых» ДВС» не дописана, окончание должно быть: «а заряд намного больше!».

- 15 –

Теперь интересно сравнить характеристики эквивалентов времени в нашем случае и по формуле Вишневского.

Повторим формулу Вишневского и выделим в ней эквивалент времени:

L=P*a : 2f;

где P=(Ф_вых - h⁰):360;

h⁰=(Ф_вых - Ф_пер):2;

а=558800 мм/с;

f = n _рез : 60 с ^-1;

Для этого нужно исключить из формулы элементы самого времени и скорости звука.

Скорость звука: а=558800 мм/с;

Обороты в секунду: f = n _рез : 60 с ^-1;

Время одного оборота: t = 60 : n _рез с;

Время прохождения одного углового градуса: t₀ = 1 : 6n _рез с;

Подставим в формулу Вишневского значения его составляющих и преобразуем:

L= [(Ф_вых + Ф_пер):4]* (1:6 n _рез )*558800 (мм).

Разделим полученное выражение на компоненты времени, скорости и умножим на 2 (показатель отражения волны), находим выражение эквивалента времени по Вишневскому:

Т_Виш = (Ф_вых + Ф_пер):2; (4)

Получим состояние изображенное как положение 4 на рис.8! Для большей наглядности изобразим это на диаграмме.

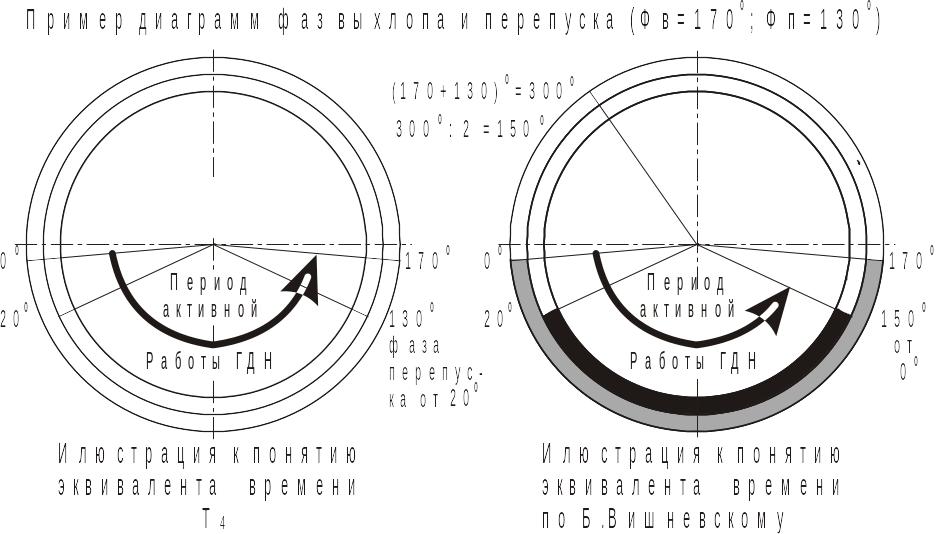
Рис. 11 Иллюстрация «понятных и непонятных» размерностей

Из изложенного выше вытекало, что формула Вишневского не совсемь адекватно отражает процесс прохождения звуковой волны в ГДН. Но формула "работала" с минимальными погрешностями при расчете высокооборотных моторов малых кубатур, уже от 3,5 см³ и выше теоретические расчеты давали чувствительную погрешность и это привело к мысли докопаться до сути. Применение резонансных глушителей в различных видах моделизма и на разных по объему двигателях, илюстрировала одну закономерность. Лучшие результаты показывались после тонкой подгонки ГДН, т.е. даже у ведущих производителей выпускаемые комплекты ДВС-глушитель, требовали доработки.

Рассмотрим вопросы возникающие при решении подобной проблемы.

Нам нужно определить:

а) длину ГДН;

- 16 -

б) объем ГДН;

в) геометрию ГДН.

Что мы имеем:

1) двигатель;

2) цель эксплуатации двигателя;

3) геометрические параметры двигателя;

4) стендовые или паспортные характеристики двигателя;

5) эксплуатационные требования к двигателю в соответствии с пунктом «2»;

6) состав топлива;

На основании тщательных замеров температуры внутри ГДН и окружающей среды, длины ГДН и частоты вращения в режиме резонанса с учетом индивидуальных геометрических характеристик ДВС методом от противного вывел величины скорости волны сжатия (термина «скорость звука» лучше избегать) для разных топлив. Для большей достоверности каждый двигатель вводился в резонанс с различными трубами и парами, обеспечивающими разброс оборотов до 40% при этом, естественно, менялась и температура и геометрия труб (длина и объем).

Имелись ХАРАКТЕРИСТИКИ 4-х моторов с трубами, ТЕМПЕРАТУРНЫЕ графики, ГЕОМЕТРИЧЕСКИЕ параметры ГДН, дополнительно те же данные для переделанных моторов. Всего однотипных данных было по 30 системам МОТОР-ГДН (3 модельных двигателя с 8 комбинациями перепускных и выхлопных окон и бензиновый мотор 22,5 см3 с моноблочной головкой, которую 5 раз перепилил и вместе со штатными окнами получил 6 комбинаций включая новые головки взамен срезанной штатной, которую пришлось удалить, чтобы расжать камеру сгорания. ЕСЛИ С ОБЪЕМАМИ ТРУБ ВСЕ СТАЛО ЯСНО ДОВОЛЬНО БЫСТРО, то проблемой стало определения АЛГОРИТМА и КОНСТАНТ. Например, что считать длиной ГДН, от зеркала поршня до мнимой середины конфузора или до еще более мнимой точки F которая неизвестно где находится. Геометрически определенней всего, все таки, вершина конфузора, какую бы форму конфузор не имел.

Что получилось см. Таблицу 3.

При испытаниях фиксировались внешние параметры (температура, влажность, давление) и геометрические параметры двигателя. В результате обработки всех данных появились вышеизложенные формулы и таблицы и, дальнейшие рассуждения. Все кривые на графиках в системе СКОРОСТЬ ВОЛНЫ-ТЕМПЕРАТУРА имеют явно выраженные черты параболл, отличающихся степенью расхождения ветвей. Величина расхождения, определяется коэффициентом «р», который мы и ищем. Для любых ТОПЛИВ можно найти величину «р» и иметь всеегда под рукой для настройки системы ДВС-ГДН.

СКОРОСТЬ ВОЛНЫ «С» В СРЕДЕ НЕКОТОРЫХ ПРОДУКТОВ СГОРАНИЯ ТОПЛИВНЫХ СМЕСЕЙ ДЛЯ 2-х ТАКТНЫХ ДВС

Таблица 3.

Высота над морем 25м. Атмосферное давление 730-735 мм рт ст. Температура среды 20⁰С. Влажность 70-80%.

Состав топлива	Минимальная температура выхлопных газов Т0К0/0С*	Скорость волны сжатия С, в м/с из эксперименов	Максимальная температура выхлопных газов Т0Кn/0С*	Скорость волны сжатия С, в м/с из эксперименов	Коэффициент р**
МЕТАНОЛ 80%; КАСТОРКА 20%	403 / 130	458,684	605 / 332	562,006	261,02809
МЕТАНОЛ 70%; КАСТОРКА 30%	387 / 114,3	447,247	581 / 308	548,000	258,43717
МЕТАНОЛ65%;КАСТ20%;НИТРО15%	453 / 180	480,761	680 / 412	601,003	255,11188
Б-95 95%; МК-22 5%	552 / 279	470,909	883 / 610	600,000	200,86573
Б-95 90%; МК-22 5%; АЦЕТОН 5%	546 / 273	462,059	873 / 600	593,000	195,51122
Форсиованное дизельное топливо с 20% масла. Из опытов 69-70 гг.	444 / 171	457,738	573 / 300	520,000	235,951

- 17 -

* Низшая и высшая среднестатистические показатели температуры при экспериментах. Минимальную температуру Т⁰К₀ можно считать базовой для дальнейших расчетов, т.к. она, практически, совпадает с температурой выхлопных газов указанных топлив для двигателей без ГДН.

** Формула для перерасчета скорости волны сжатия дана чуть ниже.

Таким образом, чтобы определить скорость волны сжатия при любой температуре (в Т⁰К- градусах Кельвина) достаточно провести простое вычисление с «р» для конкретного топлива. Сп = (2Т⁰К*р)^0,5; ⁽⁵⁾

Здесь-то и возникает вопрос, а при какой температуре нужно определять скорость?

На помощь приходят дополнительные данные, которые с достаточной точностью могут указать рабочую температуру для конкретного двигателя с конкретным топливом, при конкретных внешних условиях. Они должны заменить «Т⁰К» в формуле 5.

Сп = {2[Т⁰С-20+ Т⁰К₀]*[Р_ат+0,001(В_от- Вот₀)]*К*р)}^0,5 ; м/с (6)

где Т⁰С-20+ Т⁰К₀ - Достоверная низшая температура продуктов сгорания в ГДН, склады-

вается из температуры окружающей среды с вычетом температуры

на момент определения Т⁰К₀ и собственно, низшей температуры вы-

хлопных газов в ГДН указанной в таблице 3 .

Р_ат – атмосфкрное давление в «технических атмосферах».

1ат = 1кг/см² = 98066,5 Па = 735,561 мм рт ст;

0,001(В_от-Вот₀)- 1/1000 часть разницы между относительной влажностью окружающей

среды с относительной влажностью на момент определения Т⁰К₀. Может принять как положительное так и отрицательное значение.

К - теплонапряженность системы (см. Формулу 1)

р – индивидуальный для среды, безразмерный коэффициент (Таб.3).

Установив скорость волны сжатия определим расстояние от зеркала поршня до вершины конфузора. У нас есть расчетные обороты двигателя и данные об условиях эксплуатации. Мы определили скорость поршня и коэффициент теплонапряженности. Из таблицы 3 и с помощью формулы 5 нашли «Сп».

Длина ГДН L=0,5[1:( n _рез:60)]:360 *Cп*Фв (м); (7)

где 0,5 - показатель половины длины волны сжатия;

[1:( n _рез:60)]:360 см. Формулу 3;

Сп - скорость волны сжатия в м/с находим по формуле 5;

Фв - фаза выхлопа ДВС в угловых градусах;

n _рез - расчетная частота вращения вала мин^-1.

Зная кубатуру ДВС и скорость поршня, по графику на рисунке 7 находим объем ГДН.

Пытливый моделист (двигателист) дойдя до этой формулы спросит: «А куда девать фазы перепуска?»

Действительно, в формуле Вишневского они были, а здесь оказались не нужными. На самом деле все проще. Вернитесь к рис. 11.

Особенность классического 2-х тактного ДВС в том что фазы выхлопа и перепуска симметричные относительно ВМТ и НМТ. Волна сжатия «гуляет» (при правильной настройке) тоже симметрично (от момента приоткрытия выхлопного окна до момента закрытия). Величина выхлопного окна влияет на быстроходность мотора, а перепуск на мощность. Оба окна нельзя до бесконечности увеличивать. Фаза выхлопа в первую очередь связана с эксплуатационными требованиями к ДВС, а фаза перепуска, при этом, должна быть максимальной. Но какой? Обратимся к фактам. За ВРЕМЯ выхлопа, одновременно происходят продувка цилиндра, вытеснение рабочей смеси из цилиндра и возвращение рабочей смеси из ГДН в цилиндр. Самое время вспомнить, что поршень движется не с постоянной скоростью, а от 0 м/с в НМТ до максимума по синусоиде. Мы до сих пор говорили только о средней скорости поршня, и все расчеты велись от средней скорости, что

- 18 -

абсолютно корректно для волны сжатия и прочих процессов в ГДН. Чего нельзя сказать о процессах в двигателе. Попытка теоретического обоснования займет много места. Сошлюсь только на принцип из газовой динамики – потери давления в потоке пропорциональны квадрату скорости движения смеси, в данном случае, в перепускных окнах. Следовательно максимальная площадь перепускных окон обеспечивает наименьшие потери, а вместе с ними и лучшее наполнение надпоршневого пространства свежей смесью. Из принципа неразрывности потока, следует, что весь объем надпоршневого пространства, с момента приоткрытия перепуса, заполнен двумя средами, замещающими одна другую. Скорость этого замещения зависит от соотношения площадей окон к объему пространства: чем больше выхлопное окно, тем быстрее по времени выходят продукты сгорания, и чем больше перепускные окна, тем быстрее и качественнее происходит замещение.

Какая минимальная (максимальная) разница должна быть между высотами выхлопа и перепуска?

Одинаковая высота исключается в виду вопиющей очевидности перерасхода топлива и максимального смешания горючей смеси с продуктами сгорания.

Опытным путем (методом постепенного увеличения высоты перепуска при фиксированной высоте выхлопного окна) пришел к выводу, что наивысшие результаты при всех вариантах фаз выхлопа от 160⁰ до 220⁰ (через 10⁰) по мощности, получались при высоте перепуска равного ½ пути пройденного поршнем, т.е. высота перепускных окон должна рав-няться 0,5 высоты выхлопного окна. Особо подчеркиваю, это только для двигателей с газо-динамическим насосом на выхлопе. Как это выглядит по фазам см. Рис. 12 и Таблицу 4.

Н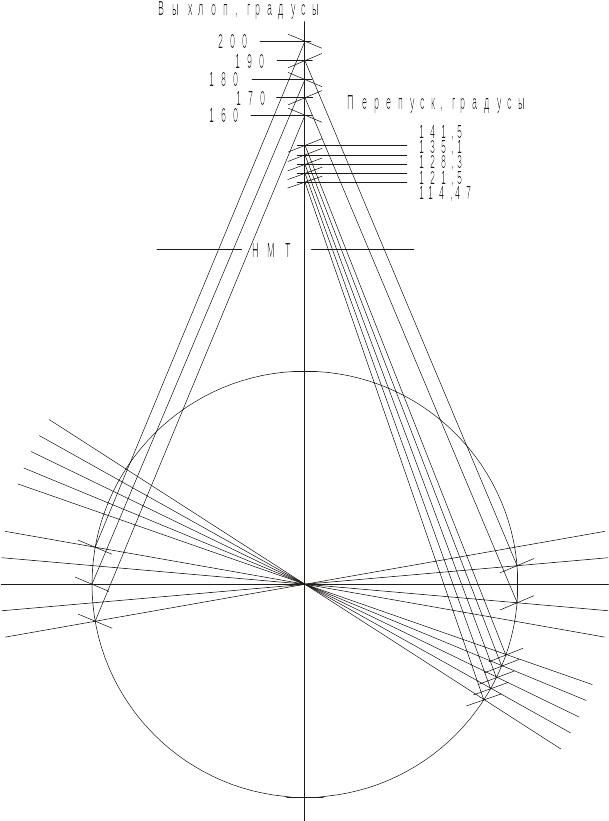 екоторая разница в величинах фаз перепуска на рисунке и в таблице объясняется достаточно большой разницей соотношений длины шатуна к ходу поршня. Это сделано специально, чтобы обратить внимание на сам фактор. В конце статьи будет показана методика точного расче-та фаз по известным линейным размерам и обратная задача, расчет высоты окон по заданным фазам, ходу поршня и длине шатуна.

Интересная деталь – при зажатых фазах, в этих пропорциях, можно делать эффективные двигатели с достаточным крутящим моментом, для пилотажников.

Пилотажный мотор с ГДН можно настроить на жестко ограниченные обороты, при правильном подборе винта это даст возможность сделать скорость полета максимально постоянной незави-симо от траектории полета.

Не знаю кто придумал, что ГДН на малых оборо-тах не эффективен. Эффекты бывают разные.

Рис.12. Иммитация фаз ВЫХЛОПА Смотря кому, что нужно.

Таблица 4

№	Выхлоп в угловых 0	Перепуск в угловых 0*	№	Выхлоп в угловых 0	Перепуск в угловых 0*	№	Выхлоп в угловых 0	Перепуск в угловых 0*
1	140	89	7	170	111	13	200	132
2	145	93	8	175	115	14	205	135,5
3	150	96,5	9	180	118	15	210	139
4	155	100	10	185	121,5	16	215	142
5	160	104	11	190	125	17	220	145
6	165	107,5	12	195	129	18	225	148

* С учетом влияния длины шатуна на соотношение фаз, эти величины приблизительны

- 19 -

Теорию закончили, начнем практическое осуществление проекта ГДН. Об идеальном ГДН в моем представлении, уже писал. Зная параметры объема и длины ГДН можно нари-совать множество геометрий отличающихся пропорциями и степенью апроксимации, т.е. приближения к плавным обводам. За основу геометрического построения ГДН я беру простую фигуру, названную мной «единичный ГДН». Единичный ГДН представляет собой некую геометрическую фигуру с известными (определяемыми) параметрами длины и объема. Для изображения реального ГДН с вычесленными параметрами длины и объема, достаточно «растянуть и раздуть» единичный ГДН. Что мы и сделаем.

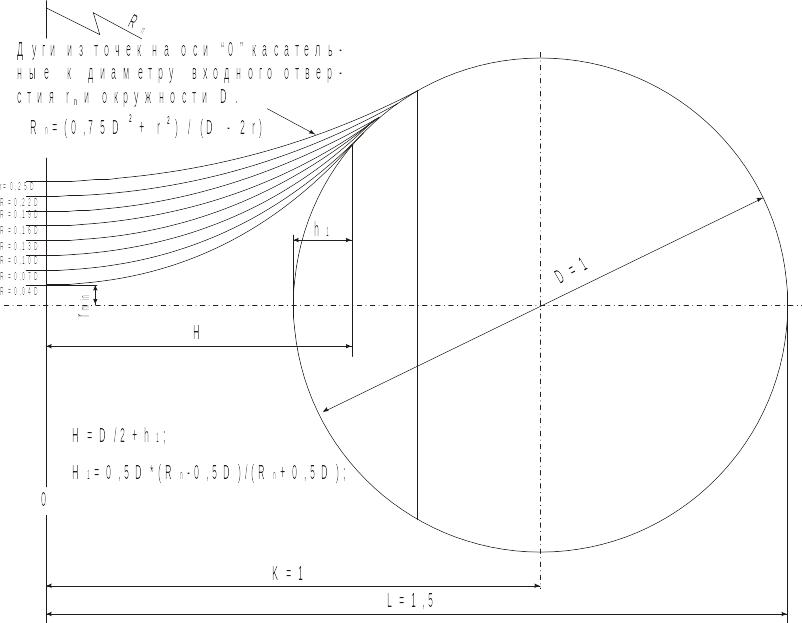
Рис. 13 Единичный газодинамический насос



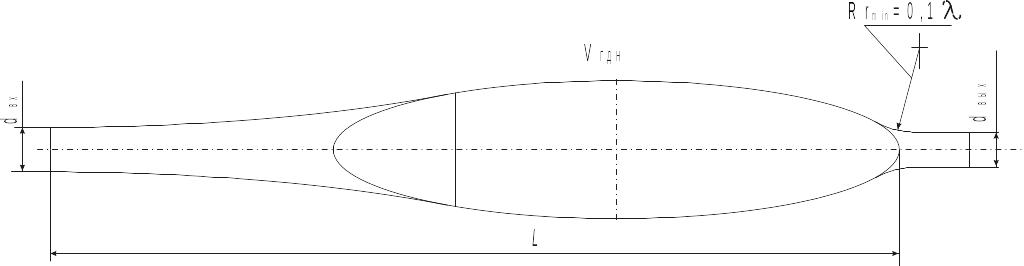
Рис.14. Единичный ГДН после преобразований. Окончательная геометрия

А теперь, как это получилось?

Единичный ГДН представляет собой совакупность двух объемов: диффузора и камеры, в различных соотношениях диаметров камеры к диаметру впускного отверстия. Диаметр камеры равен ЕДИНИЦЕ (например 1 см), остальные размеры в долях диаметра. Объемы конфигураций с различными соотношениями диаметров камеры к диаметру впускного отвер-стия даны в тех же единицах. В данном случае в СМ³.

Выполняя последовательно простые арифметические действия мы можем с достаточной точностью определить основные геометрические параметры требуемого ГДН.

Иногда для этого потребуется два и более повтора некоторых шагов. Связано это с непропорциональностью расчетного диаметра камеры ГДН с конструктивными размерами выхлопного окна конкретного двигателя.

- 20 -

СООТНОШЕНИЯ ОСНОВНЫХ РАЗМЕРОВ ЕДИНИЧНОГО ГДН

Таблица 4

№/№	dвх – диаметр входа (см)	rвх – радиус входа (см)	VГДН – объем единичной ГДН (см3)	R – радиус образующей диффузора (см)	L – длина единичного ГДН (см)
1	0,080	0,040	0,5428110	0,8169565	1,5
2	0,110	0,055	0,5495420	0,8460955	1,5
3	0,140	0,070	0,5564771	0,8777906	1,5
4	0,170	0,085	0,5636448	0,9123192	1,5
5	0,200	0,100	0,5714550	0,9500000	1,5
6	0,230	0,115	0,5788251	0,9912012	1,5
7	0,260	0,130	0,5867141	1,0365130	1,5
8	0,290	0,145	0,5954985	1,0859507	1,5
9*	0,320	0,160	0,6047544	1,1405882	1,5
10	0,350	0,175	0,6144549	1,2009615	1,5
11	0,380	0,190	0,6256917	1,2679032	1,5
12	0,410	0,205	0,6366658	1,3424152	1,5
13	0,440	0,220	0,6496533	1,4257142	1,5
14	0,470	0,235	0,6621079	1,5192924	1,5
15	0,500	0,250	0,6763178	1,6250000	1,5
16	0,530	0,265	0,6919999	1,7451595	1,5
17	0,560	0,280	0,7090538	1,8827272	1,5

*Выделена средняя строка, удобная для начального варианта расчетов.

Чертим ГДН.

1. По формуле 7 нашли длину ГДН, допустим 284 мм;

2. Зная скорость поршня, по графику рис.9 определяем объем ГДН, 89 см³:

3. Делим расчетную длину ГДН на длину единичного ГДН: 28,4 / 1,5 = 18,9333333;

4. Умножаем полученную величину на усредненный объем единичного ГДН (строка 9):

18,9333333 * 0,6047544 = 11,450016;

5. Делим расчетный объем ГДН на полученную величину:

89 / 11,450016 = 7,7729149

6. Полученная величина есть квадрат кратности диаметров искомого ГДН к единичному.

Извлекаем корень квадратный: 7,7729149^0,5 = 2,7879947;

7. Внутренний диаметр входного отверстия ГДН (по мотору), допустим 11,3 мм., Если мы

увеличим диаметр выбранного единичного ГДН в 2,7879947 раза, получим всего 8,92 ;

8. Следующий шаг, второе приближение: 11,3 / 2,788 = 4,053...

9. Выбираем из таблицы 4, ряд с ближайшим диаметром – 0,41 это будет 12-ая строка.

10. Повторяем шаг 4, теперь умножая 18,9333333 * 0,6366658 = 12,054205;

11. Делим расчетный объем ГДН на полученную величину:

89 / 12,054205 = 7,3833156;

12. Извлекаем корень квадратный: 7,3833156^0,5 = 2,7172257;

13. Диаметры входа единичного ГДН (строка 12) умножим на результат п.12: 4,1 * 2,7172257 = 11,140625;

Полученный результат на 0,15 мм меньше требуемого. Принимаем решение:

а) увеличить диаметр входного отверстия до 11,3 мм, плавно сопрягая с остальной геометрией;

б) провести самостоятельное построение геометрии .

ПРИМЕЧАНИЕ: итоговый результат будет идентичным, поправка ничтожно мала!

14. Вычерчиваем геометрию ГДН любым известным способом. Быстрее и точнее на ПК в

любой графической программе, а можно и карандашом с линейкой;

15. Расчитываем и строим оконечность ГДН:

- 21 -

Диаметр отверстия выпускного патрубка находящегося в неподвижной среде (без

эжекции)

d_вых = [(Ф_в * V^1/3_ДВС *n ) / (K^1/3_ГДН * 55673)]^0,5; мм (8)

где: Ф_в- фаза выхлопа, V^1/3_ДВС – корень кубический из объема мотора, n - обороты двигателя

K^1/3_ГДН – корень кубический из показателя кратности объема ГДН (рис.9), 55673 – безразмерный коэффициент.

Площадь выпускного отверстия : S₀ = (d_вых /2)2*; мм²

Площадь отверстия находящегося в потоке с установившейся скоростью V км/час:

S_V = S₀ – [(S₀ * V) / 657 ] мм² (9)