Задачи для самостоятельной работы:

З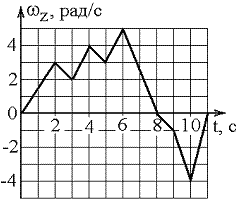 адание 1. Твердое тело начинает вращаться вокруг оси Z с угловой скоростью, проекция которой изменяется во времени, как показано на графике. Угол поворота тела относительно начального положения будет наибольшим в момент времени, равный…

1) 6 с 2) 10 с 3) 11 с 4) 8 с

З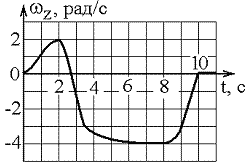 адание 2. Диск радиуса R начинает вращаться из состояния покоя в горизонтальной плоскости вокруг оси Z, проходящей перпендикулярно его плоскости через его центр. Зависимость проекции угловой скорости от времени показана на графике. Тангенциальные ускорения точки на краю диска в моменты времени t₁ = 2с и t₂ = 7с …

1) равны нулю;

2) отличаются в два раза;

3) отличаются в четыре раза;

4) равны друг другу, но не равны нулю.

Задание 3. Диск вращается вокруг своей оси, изменяя проекцию своей угловой скорости так, как показано на рисунке. Вектор угловой скорости и в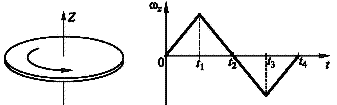 ектор углового ускорения направлены в одну сторону в интервале времени …

1. всегда направлены в одну сторону;

2. от 0 до t₁ и от t₁ до t₂ .

3. от t₁ до t₂ и от t₂ до t₃;

4. от 0 до t₁ и от t₂ до t₄;

З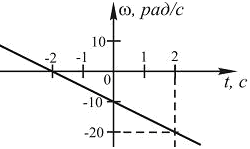 адание 4. Тело вращается вокруг неподвижной оси. Зависимость угловой скорости от времени показана на рисунке. Угловое ускорение точек тела равно …

1) – 0,5 рад/с² 2) 0,5 рад/с²

3) – 5 рад/с² 4) 5 рад/с²

Задание 5. Частица движется вдоль окружности радиусом R = 1м в соответствии с уравнением , где - в радианах, - в секундах. Частица остановится в момент времени (в с), равный …

1) 3 2) 1 3) 2 4) 4

Задание 6. Частица движется вдоль окружности радиусом R = 1м в соответствии с уравнением , где - в радианах, - в секундах. Угловое ускорение частицы ( в с^-2 ) через 3 с после начала движения равно …

1) 2) 3) 0 4)

Задание 7. Уравнение вращения твердого тела . Угловое ускорение частицы через 2 с после начала движения равно …

1) 12 рад/с² 2) 24 рад/с² 3) 48 рад/с² 4) 51 рад/с²

Коды верных ответов:

Номер задания	1	2	3	4	5	6	7
ответ	4	1	4	3	1	4	1

Динамика точки и поступательного движения твердого тела

Примеры ответов на задания

Пример 1. 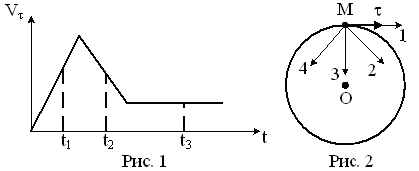Материальная точка М движется по окружности со скоростью . На рис.1 показан график зависимости от времени ( - единичный вектор положительного направления, - проекция на это направление). На рис.2 укажите направление силы, действующей на т. М в момент времени .

Ответ: Поскольку точка движется по окружности, у нее есть нормальное ускорение, направленное к центру окружности. Из графика видно, что величина скорости вблизи момента времени увеличивается, поэтому тангенциальное ускорение направлено по скорости. Полное ускорение имеет направление 2, а по второму закону Ньютона направление силы совпадает с направлением ускорения.

Ответ: 2.

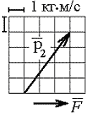Пример 2. На теннисный мяч, который летел с импульсом , на короткое время подействовал порыв ветра с постоянной силой и импульс мяча стал равным ( масштаб и направление указаны на рисунке). Величина импульса была равна …

1) ; 2) ; 3) ; 4) ; 5) .

О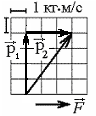 твет: Из второго закона Ньютона, записанного в импульсной форме, видно, что разность векторов начального и конечного импульсов равна импульсу силы, действующей на тело. .Эту разность можно нарисовать в приведенной координатной сетке. Импульс силы по модулю равен , а модуль конечного импульса . Из построения видно, что величина вектора была равна .

Ответ: 1.

Пример 3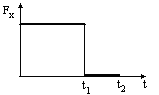 . Материальная точка двигалась вдоль оси Х равномерно с некоторой скоростью V_x. Начиная с момента времени t=0, на нее стала действовать сила F_х, график временной зависимости которой представлен на рисунке.

График, правильно отражающий зависимость величины проекции импульса материальной точки от времени, будет …

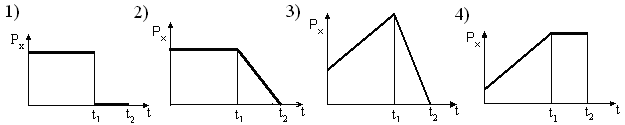
Ответ: Второй закон Ньютона можно записать: . Величина равнодействующих сил определяет скорость изменения импульса тела. На интервале времени от 0 до постоянна и положительна, следовательно величина импульса будет увеличиваться по линейному закону. На следующем интервале времени от до , следовательно,

величина импульса не будет изменяться. Такое поведение функции соответствует графику № 4

Ответ: 4.