
- •№1. Случайные события. Классификация. Действия над событиями.
- •№2. Аксиоматическое определение вероятности. Аксиомы Колмогорова. Следствия.
- •№3. Классическое, геометрическое и статистическое определения вероятности как частный случай аксиоматического.
- •№4. Теорема сложения. Следствия.
- •Теорема доказана.
- •№7. Формула полной вероятности и формула Байеса. Примеры.
- •№8. Схема независимых испытаний Бернулли. Теорема Пуассона. Предельная теорема Муавра-Лапласа.
- •№9. Случайная величина. Функция распределения случайной величины и её свойства.
- •№12. Математическое ожидание случайной величины и функции случайной величины. Свойства.
- •№14. Основные законы распределения: нормальный, равномерный, биномиальный, показательный, Пуассона.
- •№15. Векторный случайные величины, совместная плотность, многомерная вероятность, многомерный ряд распределения.
- •№16. Нормальный случайный вектор.
- •№17. Условные вероятности и плотности вероятностей. Независимость случайных величин.
- •№20. Ряд распределения функции дискретной случайной величины.
- •№21. Плотность вероятности функции случайной величины при заданной плотности вероятности аргумента. Закон распределения суммы случайных величин. Пример.
- •24. Распределения , Стьюдента (Госсета), Фишера. Их характеристики и свойства.
- •№27. Случайная выборка и генеральная совокупность. Закон распределения выборки.
- •№28. Оценка вероятности события. Оценка функции распределения. Оценка плотности вероятностей.
- •№29. Выборочные моменты. Несмещённость выборочного среднего как оценки математического ожидания. Смещённость выборочной дисперсии как оценки теоретической дисперсии.
- •№30. Точечные оценки и их свойства.
- •№31. Функция правдоподобия. Неравенство Рао-Крамера. Критерий эффективности Рао-Крамера.
- •№37. Критерий согласия . Пример.
№15. Векторный случайные величины, совместная плотность, многомерная вероятность, многомерный ряд распределения.
 – многомерная случайная величина
(упорядоченная совокупность случайных
величин). Пример – абсцисса и ордината
при случайном попадании (двумерная
случайная величина).
– многомерная случайная величина
(упорядоченная совокупность случайных
величин). Пример – абсцисса и ордината
при случайном попадании (двумерная
случайная величина).
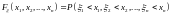 – функция распределения (совместная,
– функция распределения (совместная,
 функция распределения),
функция распределения),
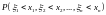 – многомерная вероятность.
– многомерная вероятность.
Рассмотрим свойства двумерной функции распределения:
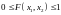 ;
; – неубывающая
функция по каждому из аргументов
и
;
– неубывающая
функция по каждому из аргументов
и
; ;
; ;
; ;
;– непрерывная слева в любой точке
 по каждому из аргументов
и
функция;
по каждому из аргументов
и
функция; .
.
Совместная плотность распределения.
Непрерывной
двумерной случайной величиной
 называют такую двумерную случайную
величину
,
совместную функцию распределения
называют такую двумерную случайную
величину
,
совместную функцию распределения
 которой можно представить в виде
сходящегося несобственного интеграла:
которой можно представить в виде
сходящегося несобственного интеграла:
 .
Функцию
.
Функцию
 называют совместной двумерной плотностью
распределения случайных величин
называют совместной двумерной плотностью
распределения случайных величин
 и
и
 ,
или плотностью распределения случайного
вектора
.
Представление в виде повторного
интеграла:
,
или плотностью распределения случайного
вектора
.
Представление в виде повторного
интеграла:
 .
.
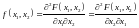
Свойства двумерной плотности распределения:
 ;
;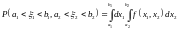 ;
;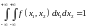 – условие
нормировки;
– условие
нормировки;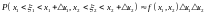 ;
; ;
; ;
;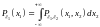 ;
;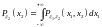 .
.
Многомерный ряд распределения.
Двумерную
случайную величину
 называют дискретной, если каждая из
случайных величин
называют дискретной, если каждая из
случайных величин
 и
является дискретной.
и
является дискретной.
 Для
простоты ограничимся конечным множеством
возможных значений, когда случайная
величина
может принимать только значения
Для
простоты ограничимся конечным множеством
возможных значений, когда случайная
величина
может принимать только значения
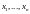 ,
– значения
,
– значения
 ,
а координаты двумерного случайного
вектора
– пары значений
,
а координаты двумерного случайного
вектора
– пары значений
 .
Такое перечисление удобно представлять
в виде таблицы. В этой таблице в верхней
строке перечислены все возможные
значения
.
Такое перечисление удобно представлять
в виде таблицы. В этой таблице в верхней
строке перечислены все возможные
значения
 случайной величины
,
а в левом столбце – значения
случайной величины
,
а в левом столбце – значения
 случайной величины
.
На пересечении столбца «
случайной величины
.
На пересечении столбца « »
со строкой «
»
находится вероятность
»
со строкой «
»
находится вероятность
 .
В этой таблице обычно добавляют ещё
одну строку «
.
В этой таблице обычно добавляют ещё
одну строку « »
и столбец «
»
и столбец « ».
На пересечении столбца
со строкой «
»
записывают число
».
На пересечении столбца
со строкой «
»
записывают число
 .
Но
.
Но
 представляет собой не что иное, как
вероятность того, что случайная величина
примет значение
,
т.е.
представляет собой не что иное, как
вероятность того, что случайная величина
примет значение
,
т.е.
 .
Таким образом, первый и последний столбцы
таблицы дают нам ряд распределения
случайной величины
.
Аналогично, в последней строке «
»
помещены значения
.
Таким образом, первый и последний столбцы
таблицы дают нам ряд распределения
случайной величины
.
Аналогично, в последней строке «
»
помещены значения
 ,
а первая и последняя строки дают ряд
распределения случайной величины
.
Для контроля правильности составления
таблицы рекомендуется просуммировать
элементы последней строки и последнего
столбца. Если хотя бы одна из этих сумм
не будет равна единице, то при составлении
таблицы была допущена ошибка.
,
а первая и последняя строки дают ряд
распределения случайной величины
.
Для контроля правильности составления
таблицы рекомендуется просуммировать
элементы последней строки и последнего
столбца. Если хотя бы одна из этих сумм
не будет равна единице, то при составлении
таблицы была допущена ошибка.
Используя
данную таблицу, нетрудно определить
совместную функцию распределения
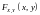 .
Ясно, что для этого необходимо
просуммировать
.
Ясно, что для этого необходимо
просуммировать
 по всем тем
и
по всем тем
и
 ,
для которых
,
для которых ,
т.е.
,
т.е.
 .
.
№16. Нормальный случайный вектор.
Введём
двумерное нормальное распределение
случайного вектора
 .
.
Пусть
координаты
 и
и
 случайного вектора
являются случайными величинами,
распределёнными по нормальному закону,
т.е. имеют плотности распределения
случайного вектора
являются случайными величинами,
распределёнными по нормальному закону,
т.е. имеют плотности распределения
 и
и
 .
Если
и
являются независимыми случайными
величинами, то
.
Если
и
являются независимыми случайными
величинами, то
 ,
и в этом случае плотность распределения
двумерного нормального распределения
имеет вид
,
и в этом случае плотность распределения
двумерного нормального распределения
имеет вид
 .
В общем случае вектор
имеет (невырожденное) двумерное нормальное
распределение, если его плотность
распределения определяется формулой
.
В общем случае вектор
имеет (невырожденное) двумерное нормальное
распределение, если его плотность
распределения определяется формулой
 ,
где функция двух переменных
,
где функция двух переменных
 есть положительно определённая
квадратичная форма (т.е.
есть положительно определённая
квадратичная форма (т.е.
 для любых
для любых
 ).
).
Двумерное нормальное распределение зависит от пяти параметров:
– координат
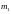 и
и
 вектора
вектора
 ,
называемого вектором математических
ожиданий вектора
;
,
называемого вектором математических
ожиданий вектора
;
–
координат
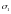 и
и
 вектора
вектора
 ,
называемого вектором средних квадратических
отклонений вектора
;
,
называемого вектором средних квадратических
отклонений вектора
;
–
числа
 ,
называемого коэффициентом корреляции
случайных величин
и
.
,
называемого коэффициентом корреляции
случайных величин
и
.
