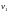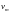- •№1. Случайные события. Классификация. Действия над событиями.
- •№2. Аксиоматическое определение вероятности. Аксиомы Колмогорова. Следствия.
- •№3. Классическое, геометрическое и статистическое определения вероятности как частный случай аксиоматического.
- •№4. Теорема сложения. Следствия.
- •Теорема доказана.
- •№7. Формула полной вероятности и формула Байеса. Примеры.
- •№8. Схема независимых испытаний Бернулли. Теорема Пуассона. Предельная теорема Муавра-Лапласа.
- •№9. Случайная величина. Функция распределения случайной величины и её свойства.
- •№12. Математическое ожидание случайной величины и функции случайной величины. Свойства.
- •№14. Основные законы распределения: нормальный, равномерный, биномиальный, показательный, Пуассона.
- •№15. Векторный случайные величины, совместная плотность, многомерная вероятность, многомерный ряд распределения.
- •№16. Нормальный случайный вектор.
- •№17. Условные вероятности и плотности вероятностей. Независимость случайных величин.
- •№20. Ряд распределения функции дискретной случайной величины.
- •№21. Плотность вероятности функции случайной величины при заданной плотности вероятности аргумента. Закон распределения суммы случайных величин. Пример.
- •24. Распределения , Стьюдента (Госсета), Фишера. Их характеристики и свойства.
- •№27. Случайная выборка и генеральная совокупность. Закон распределения выборки.
- •№28. Оценка вероятности события. Оценка функции распределения. Оценка плотности вероятностей.
- •№29. Выборочные моменты. Несмещённость выборочного среднего как оценки математического ожидания. Смещённость выборочной дисперсии как оценки теоретической дисперсии.
- •№30. Точечные оценки и их свойства.
- •№31. Функция правдоподобия. Неравенство Рао-Крамера. Критерий эффективности Рао-Крамера.
- •№37. Критерий согласия . Пример.
№37. Критерий согласия . Пример.
Постановка задачи.
Имеется
некоторая случайная величина
,
распределённая по закону
.
Формулируется утверждение
 (1),
где
(1),
где
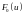 – предполагаемая функция распределения.
(1) – основная гипотеза (утверждение о
том, что
имеет конкретный вид). Ей противопоставляется
гипотеза
(она содержит все распределения, которые
могут быть, но не соответствуют основной
гипотезе) – альтернативная гипотеза
(
– предполагаемая функция распределения.
(1) – основная гипотеза (утверждение о
том, что
имеет конкретный вид). Ей противопоставляется
гипотеза
(она содержит все распределения, которые
могут быть, но не соответствуют основной
гипотезе) – альтернативная гипотеза
(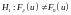 ).
).
Критерий
согласия
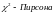 .
.
Чтобы использовать данный критерий, необходимо составить группированную выборку:
|
|
|
|
|
|
|
|
|
|
|
|
Составляется
статистика
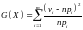 – статистика Пирсона (
– статистика Пирсона ( –
практическое значение выборки,
– объём выборки,
– вероятность попадания в
–
практическое значение выборки,
– объём выборки,
– вероятность попадания в
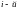 интервал, исходя из предположения закона
распределения).
интервал, исходя из предположения закона
распределения).
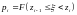
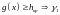 (отвергнуть
основную гипотезу и принять альтернативу),
(отвергнуть
основную гипотезу и принять альтернативу),
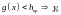 (принять
основную гипотезу). Здесь
(принять
основную гипотезу). Здесь
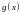 – значение статистики,
– значение статистики,
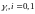 – выводы,
– выводы,
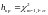 – квантиль распределения
с
– квантиль распределения
с
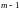 степенями свободы порядка
степенями свободы порядка
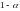 ,
где
,
где
 – уровень значимости критерия (вероятность
отвергнуть гипотезу
– уровень значимости критерия (вероятность
отвергнуть гипотезу
 ,
если она на самом деле верна).
,
если она на самом деле верна).
Пример:
Произведено 4040 подбрасываний монеты.
Герб выпал 2048 раз. Справедлива ли при
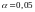 гипотеза о том, что монета симметрична?
гипотеза о том, что монета симметрична?
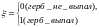 ;
;
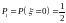 ;
;
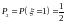 ;
;
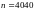 ;
;
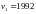 ;
;
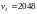
Подставляем
значения:
 .
.
 (из таблицы),
(из таблицы),
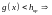 необходимо
принять основную гипотезу (монета
симметрична).
необходимо
принять основную гипотезу (монета
симметрична).