43

№1. Случайные события. Классификация. Действия над событиями.

Предметом изучения ТВ является закономерность в массовых случайных явлениях.

Явление называется массовым, если его, теоретически, можно наблюдать неограниченное количество раз в одинаковых условиях.

Исход случайного явления заранее не предопределён. Для описания случайных явлений строится математическая модель – вероятностная модель.

Опыт (эксперимент, наблюдение) – наблюдение некоторого явления при фиксированных условиях.

Факт, регистрируемый в результате опыта, называется событием.

Если факт был зарегистрирован, то говорят, что событие появилось, или возникло.

Случайное событие – событие, о котором заранее не известно, произойдёт оно или нет.

Случайные события обозначаются заглавными латинскими буквами:

Классификация случайных событий.

1. Событие называется достоверным, если оно обязательно произойдёт в результате опыта ( );

2. Событие называется невозможным, если оно обязательно не произойдёт в результате опыта ( );

3. События называются несовместными, если они не могут происходить вместе в одном опыте;

4. Событие, противоположное – событие , состоящее в непоявлении события ;

5. События и называются благоприятствующими ( ), если появление события влечёт за собой появление события ;

6. События и эквивалентны ( ), если состоит в появлении , а – в появлении :

7. Составные события – события, сами состоящие из нескольких событий.

Действия над событиями.

1. Сумма событий ( ) – событие, которое состоит в появлении хотя бы одного из событий-слагаемых.

2. Произведение событий ( ) – событие, которое состоит в появлении обоих событий-множителей в одном опыте.

3. Разность событий ( ) – событие, состоящее в появлении и непоявлении .

События образуют полную группу, если они в сумме дают достоверное событие: .

Множество элементарных исходов (исходов, элементарных событий) – полная группа несовместных равновозможных событий.

Равновозможные события – события, каждое из которых не является более возможным, чем другие.

Свойства операций над событиями.

1⁰. Коммутативность: ;

2⁰. Дистрибутивность: ;

3⁰. Ассоциативность: .

1. ;

2. ;

3. ;

4. ;

5. .

№2. Аксиоматическое определение вероятности. Аксиомы Колмогорова. Следствия.

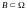Пусть – некоторое множество (множество элементарных исходов). Элементы будем обозначать , подмножества , – случайные события.

Рассмотрим 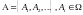– алгебра множеств, порождённая подмножествами , если:

1. ;

2. ;

3. .

– . Если условие 3 выполняется для произвольного количества множеств, то – измеримое пространство.

Аксиома 1 (аксиома неотрицательности): Каждому элементу ставится в соответствие неотрицательное вещественное число – вероятность.

Аксиома 2 (аксиома нормированности): .

Аксиома 3(аксиома сложения): .

Аксиома 4 (расширенная аксиома сложения): .

Аксиома 5 (аксиома непрерывности): .

Следствие 1: .

Доказательство: , .

Следствие 2: .

Доказательство: .

Следствие 3 (теорема сложения): .

Доказательство: Следствие 4 (неравенство треугольника): .

Следствие 5: .

Доказательство: .

Следствие 6: .

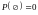Доказательство: .