4.Определение углов наклона прямой к плоскостям проекций. Следы прямых.

Угол прямой линии с плоскостью проекции определяется как угол, составленный прямой с ее проекцией на этой плоскости. Этот угол входит в тот же прямоугольный треугольник, который строят для определения Н.В. отрезка.

Следом прямой линии называется точка, в которой прямая пересекается с плоскостью проекций (так как след - точка, принадлежащая одной из плоскостей проекций, то одна из её  координат должна быть равна нулю).

Горизонтальный след - точка пересечения прямой с горизонтальной плоскостью проекций.

Фронтальный след - точка пересечения прямой с фронтальной плоскостью проекций.

Профильный след - точка пересечения прямой с профильной плоскостью проекций.

7.Проекции плоских углов:

1.Если пл-ть в которой расположен некоторый угол перпендик.К пл-ти проекции,то он проецируется на эту пл-ть в виде прямой.

2.Если стороны угла // пл-ти проекции,то угол проецируется в свою величину.

3.Если пл-ть прямого угла не перпендикулярна к пл-ти проекции и хотя бы одна сторона угла // этой пл-ти, то прямой угол проецируется на пл-ть в виде прямого же угла.

4.Если проекция плоского угла представляет собой прямой угол,то проецируемый угол будет прямым лишь при условии что хотя бы одна из сторон угла параллельна пл-ти проекции

5.Если проекция некоторого угла у которого одна сторона // пл-ти проекции представляет собой прямой угол, то проецируемый угол тоже прямой

10.Особые линии плоскости

Прямые уровня - это прямые, принадлежащие плоскости и параллельные какай - либо плоскости проекций. Эти прямые называют прямыми уровня, так как они принадлежат плоскости уровня. Существует три вида прямых уровня:

h - горизонталь плоскости - прямая принадлежащая данной плоскости и || плоскости проекций 1;

f - фронталь плоскости - прямая принадлежащая данной плоскости и || плоскости проекций 2;

w - профильная прямая плоскости - прямая принадлежащая данной плоскости и || плоскости проекций 3.

Прямая, принадлежащая плоскости и к горизонтали, фронтали или профильной прямой, называется линией наибольшего наклона плоскости к плоскости проекций П₁, П₂ или П₃. Линию наибольшего наклона к плоскости проекций П₁ называют линией наибольшего ската.

5.Взаимное положение прямых в пространстве

Две прямые в пространстве могут пересекаться, скрещиваться и могут быть параллельны.

1. Пересекающиеся прямые

Пересекающимися прямыми называются такие прямые, которые имеют одну общую точку.

2. Параллельные прямые

параллельные прямые – прямые, пересекающиеся в несобственной точке (прямые, лежащие в одной плоскости и пересекающиеся в бесконечно удаленной точке).

3.Скрещивающиеся прямые

Скрещивающиеся прямые – это прямые, которые не // и не пересекаются между собой.

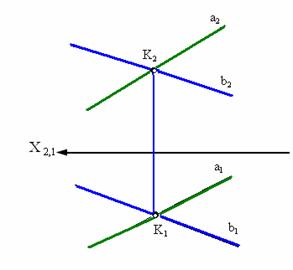
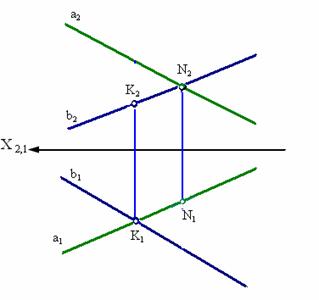
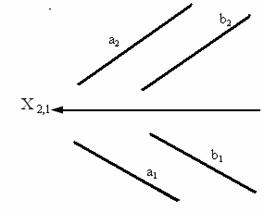
6.Скрещивающиеся прямые. Видимость скрещ.Прямых.

Скрещивающиеся прямые – прямые, которые не // и не пересекаются между собой.

Точка пересечения одноименных проекций скрещ. прямых представляет собой проекции двух точек из которых одна принадлежит первой, а другая - второй из этих скрещ. прямых.

Если видно что на одной проекции точки совпадают, а на другой четко видно, что проекции принадлежат разным отрезкам, нужно определять видимость. Точка которая находится дальше от плоскости проекции (т.1) и закрывает собой другую точку(т.2) будет видимой. => т.2 невидимая. Такие точки называются конкурирующими.

8.

Способы задания пл-ти:

1.3-мя точками не лежащими на одной прямой.

2.Прямой и точкой, вне этой прямой.

3.Пересекающимися прямыми.

4.Двумя //прямыми

5.Любой плоской фигурой.

6.Параметрами

7.Следами

Следы пл-ти – прямые по которым некоторая пл-ть пересекает пл-ти проекций.

9.положение плоскости относительно плоскостей проекций

В зависимости от положения плоскости по отношению к плоскостям проекций она может занимать как общее, так и частные положения.

Плоскость не перпендикулярная ни одной плоскости проекций называется плоскостью общего положения.  Такая плоскость пересекает все плоскости проекций (имеет три следа: - горизонтальный ; фронтальный ; профильный).

Плоскости, перпендикулярные плоскостям проекций – занимают частное положение в пространстве и называются проецирующими. В зависимости от того, какой плоскости проекций перпендикулярна заданная плоскость, различают:

1.Плоскость, перпендикулярная горизонтальной плоскости проекций ,называется горизонтально проецирующей плоскостью.

2. Плоскость, перпендикулярная профильной плоскости – профильно-проецирующая плоскость.

3. Горизонтальная плоскость - плоскость, параллельная горизонтальной плоскости проекций.

4. Фронтальная плоскость - плоскость, параллельная фронтальной плоскости проекций.

5. Профильная плоскость - плоскость, параллельная профильной плоскости проекций

11.Линии наиб. Уклона и их применение.

Линией наиб. уклона плоскости называется прямая , принадлежащая этой плоскости и перпендикулярная ее линиям уровня: горизонтали h и фронтали f. На комплексном чертеже гориз. проекция линии наиб. уклона перпендикулярна гориз. проекции горизонтали этой плоскости, а фронтальная − фронтальной проекции фронтали. Главным свойством этой линии наибольшего уклона является то, что она образует с горизонтальной плоскостью проекций угол α°, равный углу наклона плоскости к плоскости. Это свойство линии наибольшего уклона используется для определения углов наклона плоскостей к плоскостям проекций.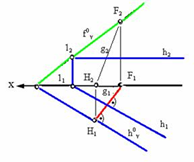

12. Прямая и точка в плоскости

В пространстве прямая может либо принадлежать плоскости, либо не принадлежать плоскости. Это утверждение справедливо и для точки. Прямая принадлежит плоскости, если она проходит:

• Через две точки, принадлежащие плоскости;

• Через точку плоскости параллельно любой прямой этой плоскости.

Точка принадлежит плоскости, если она принадлежит любой прямой в этой плоскости.

25. Встречаются случаи, когда поверхности вращения пересекаются по двум плоским кривым - эллипсам. Это бывает тогда, когда поверхности двух тел вращения описаны около сфер.

если две цилиндрические или конические, или одна коническая, а другая цилиндрическая поверхности описаны вокруг сферической поверхности (и, следовательно, оси их, пересекаясь, проходят через центр сферы), то они пересекаются по плоским кривым (эллипсам);

Пересечение поверхностей вращения: а) Конуса с конусом; б) Цилиндра с конусом: в) Тора с тором;

26.Развертка поверхности многогранников

Разверткой многогранной поверхности называется плоская фигура, получаемая последовательным совмещением всех граней поверхности с плоскостью.

Так как все грани многогранной поверхности изображаются на развертке в натуральную величину, построение ее сводится к определению величины отдельных граней поверхности – плоских многоугольников.

Существует три метода построения развертки многогранных поверхностей:

1. Метод треугольника.

2. Метод нормального сечения.

3. Метод раскатки.

27.Развертка поверхностей вращения

Развертка - плоская фигура, в которую преобразуется поверхность путем совмещения с плоскостью без разрывов и складок.

К развертываемым поверхностям относят поверхности:

•многогранников;

•линейчатые поверхности с параллельными или пересекающимися образующими, а именно - цилиндрические, конические и поверхности с ребром возврата.

Развертки многогранников относят к точным разверткам. Поверхность называется развертываемой на плоскость, если между точками поверхности и плоскости можно установить взаимно однозначное соответствие, при котором:

•каждой точке поверхности соответствует точка на развертке;

•длины соответствующих линий на поверхности и на развертке равны между собой;

•замкнутая линия на поверхности и соответствующая ей линия на развертке ограничивают одинаковую площадь;

•угол между линиями на поверхности равен углу между соответствующими им линиям на развертке;

•отрезку прямой линии на развертке соответствует геодезическая линия поверхности, кратчайшим путем соединяющая две точки на данной поверхности