3. По наличию свободной поверхности движения делятся на напорные, безнапорные и свободные.

Напорным называется движение жидкости, не имеющей свободной поверхности. Примером такого движения может служить движение жидкости в трубопроводе при полном заполнении его сечения, например воды в водопроводе.

Б

Рис. 1.13. Безнапорное течение жидкости

езнапорным движением называется движение жидкости со свободной поверхностью в открытых и закрытых руслах (Рис. 1.13). Примером такого движения может служить движение воды в реках, бытовых стоков в канализационных коллекторах. Безнапорное движение может быть разделено на спокойное, бурное и критическое в зависимости от критической глубины потока h_кр.

Для спокойного движения (течение воды в равнинных реках) глубина потока h > h_кр.; для бурного движения (течение воды в горных реках) h < h_кр.; для критического движения h = h_кр.

Свободным является движение жидкости, нигде не стесняемое твердыми стенками русла. Свободное движение жидкости называется струями. Струи могут быть затопленные и незатопленные.

Затопленной струей называется такое движение, при котором плотность движущейся жидкости примерно равна плотности окружающей среды. Например, затопленной является струя дыма, выходящая из трубы, струя промывочного раствора, бьющая из сопла гидромониторного долота. Незатопленной струей называется такое движение, при котором плотность движущейся жидкости намного превышает плотность окружающей среды. Это, например, фонтанная струя или струя воды из пожарного брандспойта.

4. Движение может быть сплошным и прерывистым. Сплошным, или непрерывным движением, называется такое движение, при котором жидкость сплошь заполняет всю область своего движения. Прерывистым является движение жидкости при наличии пустот в области движения. Обычное течение в реках  сплошное, а на водопадах  прерывистое.

5. Движение может быть осесимметричным (поле скоростей и ускорений имеет одинаковый вид в любых плоскостях, проходящих через некоторую прямую, называемую осью симметрии) и неосесимметричным. Примером осесимметричного движения может служить движение жидкости в круглых трубках.

6. Движения можно разделить на одномерные, двухмерные (плоскопараллельные) и трехмерные.

Трехмерное движение  это такое движение, когда параметры потока изменяются вдоль всех трех координат (Рис. 1.14). Трехмерное движение может быть как неустановившимся, так и установившимся.

П

Рис. 1.15. Двухмерное движение при обтекании бесконечного цилиндра

Рис. 1.14. Трехмерное движение при обтекании крыла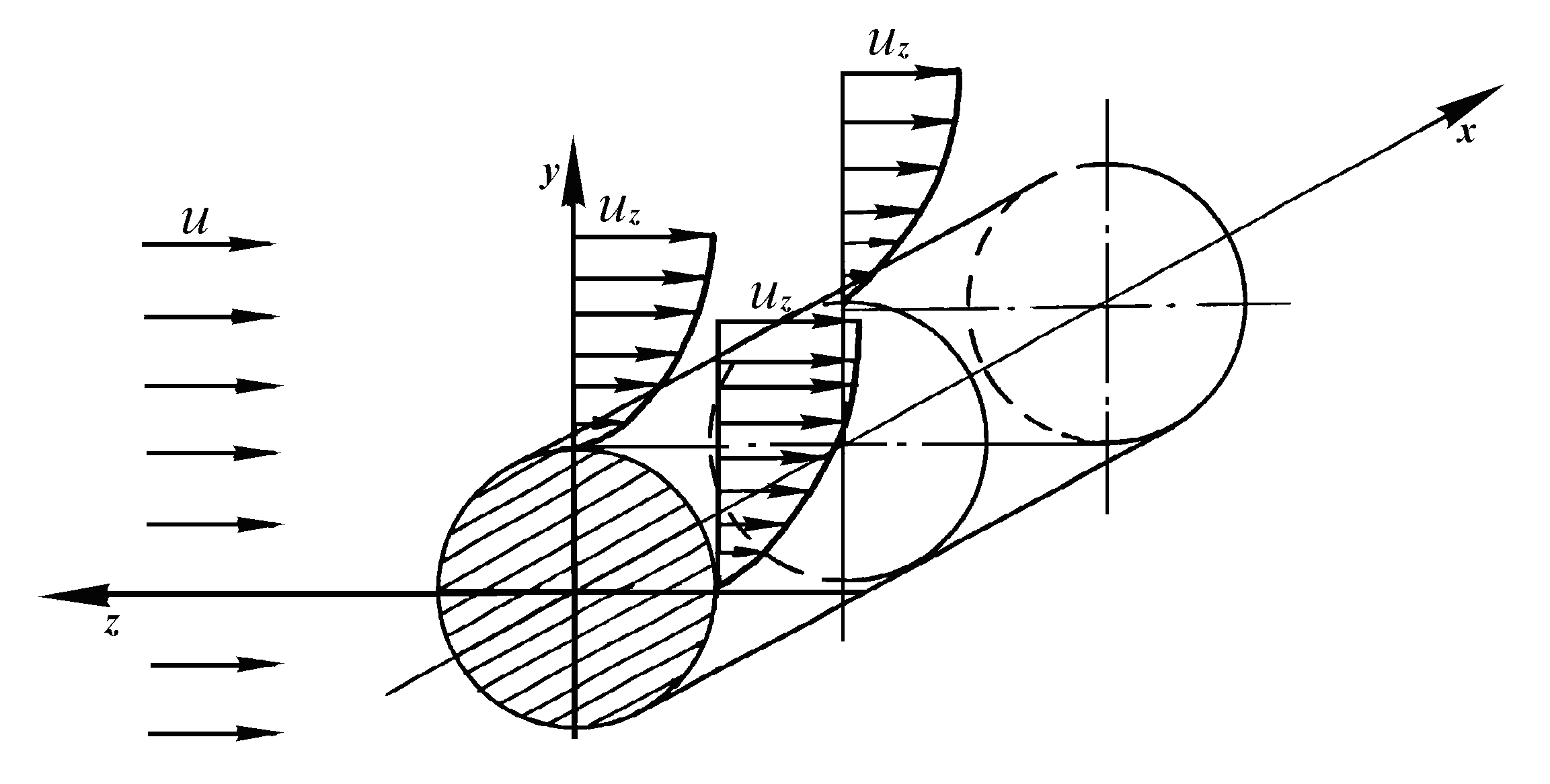

римером трехмерного движения в прямоугольной системе координат может служить обтекание потоком любого тела конечных размеров, например, крыла. Если проследить, как изменяется скорость потока вдоль каждой из трех координат, то видно, что при фиксированном значении двух любых координат (например, y = z = 0)

скорость изменяется вдоль третьей координаты. Напомним, что изменение скорости вблизи твердой поверхности обусловлено «прилипанием» частичек жидкости к этой поверхности.

Двухмерное движение  это такое движение, когда параметры потока изменяются только вдоль двух координат. Оно также может быть неустановившимся и установившимся.

Примером двухмерного движения в прямоугольной системе координат может служить обтекание потоком бесконечного цилиндра (Рис. 1.15). Нетрудно заметить, что в отличие от предыдущего случая здесь происходит изменение скоростей только вдоль осей y и z. Вдоль оси х скорость не изменяется при любых фиксированных значениях y и z.

Двухмерное движение всегда является плоскопараллельным, удовлетворяющим двум условиям:

а) в данный момент времени область движения можно пересечь такими плоскими параллельными поверхностями, в которых лежат векторы скоростей и ускорений, отвечающие всем точкам этих поверхностей;

б) во всех точках любого перпендикуляра, проведенного к указанным поверхностям, скорости и ускорения в данный момент времени одинаковы (по величине и направлению).

О

Рис. 1.16. Одномерное движение при обтекании бесконечной плоской пластины

дномерное движение  это такое движение, когда параметры потока изменяются только вдоль одной координаты.

Примером одномерного движения в прямоугольной системе координат может служить обтекание потоком бесконечной плоской пластинки (Рис. 1.16). В этом случае скорость изменяется только в направлении нормали к поверхности пластинки, т. е. вдоль координаты y. Одномерное течение также всегда является плоскопараллельным. Его называют также линейным движением.

Вполне очевидно, что одномерное движение является простейшим для анализа видом движения. При этом следует отметить, что иногда от выбора системы координат зависит, будет ли движение трехмерным, двухмерным или даже одномерным. Например, при движении жидкости в цилиндрической трубе переход от прямоугольной к цилиндрической системе координат переводит задачу из двухмерной в одномерную.

7. Движения можно классифицировать по механизму передачи количества движения между слоями жидкости. Если этот механизм имеет молекулярную природу, движение называется ламинарным. Если количество движения передается в основном за счет обмена жидкими массами, перемещающимися хаотически во всем объеме жидкости, движение называется турбулентным. Турбулентное движение можно дополнительно разделить на движение в зонах гладкого, смешанного и шероховатого сопротивления (трения).

Для лучшего представления о связи между различными видами движения на Рис. 1.17 показана классификационная схема движений по Л.С. Абрамзону, пользуясь которой, можно достаточно полно охарактеризовать любое течение.

Кинематические характеристики движения. Поток жидкости  это часть неразрывно движущейся жидкости, ограниченная твердыми деформируемыми или недеформируемыми стенками, иногда воздушной средой или жидкостью струи.

Важнейшей характеристикой (параметром) движения жидкости является ее скорость. Поскольку жидкость рассматривается как сплошная среда, состоящая из частичек, то очевидно, что при движении жидкости каждая частица обладает определенной скоростью в данной точке пространства.

Локальная (местная) скорость  скорость жидкой частички в данной точке пространства в данный момент времени, это  векторная величина.

Поле скоростей  совокупность векторов локальных скоростей, построенных для некоторого множества точек пространства в данный момент времени.

Рис. 1.17. Схема движений жидкости

Путем задания поля скоростей жидкости в пространстве в каждый момент времени определяется движение жидкости (по методу Эйлера). Например, неустановившееся движение в цилиндрических координатах

, (1.56)

в прямоугольных декартовых координатах

, (1.57)

где  скорость жидкости в момент времени в точке пространства, определяемой радиус-вектором ;  проекции скорости жидкости в момент времени в точке пространства на оси координат x, y, z; i, j, k  единичные векторы по осям координат (орты).

Для полной характеристики движения необходимы сведения об ускорении движения частичек жидкости.

Ускорение при движении жидкости вычисляется по формуле .

Математическое выражение ускорения можно получить, взяв полную производную по времени от функциональной зависимости (1.56 или 3.57) с учетом элементарного перемещения частицы жидкости dr или dx, при переходе от точки к точке. Полный дифференциал вектора скорости (1.57) как функция четырех переменных x, y, z, и равен

. (1.58)

Чтобы найти ускорение , нужно изменение скорости du разделить на d:

. (1.59)

Так как перемещения частицы жидкости dx, dy, dz не произвольны, а связаны между собой уравнением

,

то

Итак,

. (1.60)

Полная производная представляет собой полное ускорение движения данной частицы, она называется иногда субстанциональной производной.

Составляющая ускорения называется локальным ускорением, она характеризует изменение скорости в данной точке пространства и обусловлена изменением поля скоростей во времени. Очевидно, что при установившемся движении . Сумма слагаемых называется конвективным ускорением, она характеризует изменение скорости в данный момент времени вдоль линии тока и обусловлена неоднородностью поля скоростей. При установившемся равномерном движении несжимаемой жидкости в прямых каналах конвективное ускорение равно нулю.

В проекциях на оси x, y, z уравнение (1.60) примет вид

,

, (1.61)

.

Геометрическими характеристиками потока являются три линии  траектория, линия тока и линия отмеченных точек.

Траектория  линия, по которой движется некоторая частица жидкости.

Линия тока  проведенная в потоке жидкости условная линия, во всех точках которой в данный момент времени векторы локальных скоростей направлены по касательной к этой линии.

Д

Рис. 1.18. Линии тока

ля построения линии тока (Рис. 1.18) поступим следующим образом. В произвольной точке 1 построим вектор локальной скорости u₁(), соответствующий данному моменту времени . На некотором расстоянии от точки 1 на векторе u₁() выберем точку пространства 2 и для частички жидкости, находящейся в ней в этот же момент времени , построим вектор локальной скорости u₂(), на котором выберем точку 3 и так далее. Соединив плавной линией полученные точки 1, 2, 3, 4, ... мы получим линию тока. Чем ближе друг к другу будут располагаться точки, тем точнее будет построение.

В любой точке линии тока согласно построению ее элемент dS будет для данного момента времени одновременно являться и элементом пути (проекции которого на оси координат суть dx, dy, dz). Следовательно, в любой точке линии тока локальная скорость может быть определена как или в проекциях на оси координат

. (1.62)

Вычисляя из (1.62) d и приравнивая полученные выражения, получим уравнение линии тока в виде

(1.63)

Нетрудно видеть, что при установившемся движении, когда с течением времени величина и направление локальных скоростей не изменяются, линия тока совпадает с траекторией.

Из определения линии тока следует важный вывод: две линии тока в данном потоке не могут пересекаться друг с другом. Действительно, в точке пересечения можно построить два вектора локальной скорости (касательные к каждой линии тока в отдельности), принадлежащие одной и той же частичке жидкости в один и тот же момент времени, что недопустимо.

Линия отмеченных точек  линия, на которой в данный момент времени лежат частицы жидкости, прошедшие в свое время через одну и ту же начальную точку. Иллюстрацией такой линии может служить линия расположения поплавков, последовательно выпущенных из одной и той же точки.

При установившемся движении линия отмеченных точек совпадает с траекторией и линией тока.

Поверхность тока  поверхность, образованная совокупностью линий тока, проведенных через множество точек некоторой кривой, расположенной в потоке жидкости (Рис. 1.19).

Трубка тока  трубчатая поверхность тока бесконечно малого поперечного сечения, проведенная через бесконечно малый замкнутый контур (Рис. 1.20).

Важным свойством трубки тока, как и любой поверхности тока, является то, что она непроницаема для жидкости. Действительно, т. к. трубка тока образована линиями тока, то во всех ее точках скорости направлены по касательной к ней, а следовательно, частички жидкости движутся вдоль трубки тока, не пересекая ее.

Элементарная струйка  жидкость, протекающая внутри трубки тока. Вследствие непроницаемости трубки тока ни одна частица из окружающего пространства не может войти в пространство элементарной струйки.

Живым сечением элементарной струйки или потока называется плоскость сечения струйки или потока, нормальная в каждой точке своей к соответствующей линии тока.

Р

Рис. 1.19. Поверхность тока

Рис. 1.20. Трубка тока

асходом жидкости называется количество жидкости, проходящей через живое сечение потока в единицу времени. Различают объемный (м³/с), массовый (кг/с) и весовой (Н/с) расходы.

Расход элементарной струйки называется элементарным расходом.

Составим уравнение элементарного расхода (Рис. 1.21). За время d все частицы из сечения n-n переместятся на расстояние dS, равное , (u  скорость движения частиц элементарной струйки), и перейдут в сечение . При этом пространство, равное по объему , будет занято другими частицами.

Здесь df  живое сечение элементарной струйки, в пределах которой изменением скорости u можно пренебречь. Таким образом, за время d через сечение n - n проходит жидкость в объеме .

Рис. 1.21. К определению

элементарного расхода

За единицу времени проходит количество жидкости в объеме, т. е. элементарный расход, dQ, м³/с,

. (1.64)

Массовый расход , кг/с, а весовой , Н/с.

Исходя из понятия элементарной струйки можно говорить о том, что любой поток конечных размеров можно рассматривать состоящим из бесконечно большого числа элементарных струек (Рис. 1.22). Поскольку скорость течения в отдельных струйках в общем случае разная, постольку и скорость в разных точках поперечного сечения будет разной. Закон распределения скоростей характеризуется эпюрой (профилем) скоростей (Рис. 1.23).

Профиль (эпюра) скоростей  поле скоростей, построенное для множества точек живого сечения потока. Иногда рассматривают не все поле, а лишь его характерное сечение или даже просто контур этого сечения.

Рассмотрим ламинарное течение жидкости в цилиндрической трубе. Для такого течения поле скоростей живого сечения имеет вид параболоида вращения. Под профилем скоростей чаще всего понимают параболу, проходящую через концы векторов локальных скоростей, проведенных через все точки диаметра трубы.

Л

Рис. 1.22. Поток конечных размеров Рис. 1.23. Профиль скоростей

окальная скорость жидкости в некоторый момент времени называется мгновенной, а если она рассматривается за некоторый промежуток времени  осредненной. Скорость течения потока характеризуется средней скоростью по данному поперечному сечению:

, (1.65)

где расход потока, равный сумме расходов элементарных струек,

. (1.66)

Средняя скорость  это некоторая постоянная фиктивная скорость, с которой должны двигаться через поперечное сечение все частицы жидкости, чтобы ее расход равнялся расходу при движении с истинными неодинаковыми по сечению скоростями.

Из уравнения (1.65) следует уравнение расхода

Q = υ f. (1.67)

Для двух сечений 1-1 и 2-2 элементарной струйки (Рис. 1.24) в установившемся движении можно записать: и . Очевидно  по условию несжимаемости жидкости (иначе пространство между сечениями должно возрастать) и  по условию сплошности течения (иначе в указанном пространстве между сечениями образуется пустота  разрыв сплошности).

Рис. 1.24. Вывод уравнения сплошности течения

Следовательно, условие неразрывности течения запишется так:

или и , (1.68)

Для всего потока это условие будет записано в виде:

, или , (1.69)

т. е. расход потока вдоль по течению один и тот же.

При движении жидкости через площадь поперечного сечения, отличного от круглого, в качестве расчетного определяющего размера используют гидравлический радиус.

Гидравлический радиус находят по формуле

, (1.70)

где f  площадь поперечного сечения трубопровода или канала, через которую протекает жидкость, м²; n  смоченный периметр, м.

Н

Рис. 1.25. Профили прямоугольного и кольцевого каналов

апример, гидравлический радиус трубы .

Диаметр, выраженный через гидравлический радиус, называется эквивалентным диаметром.

. (1.71)

Эквивалентный диаметр равен диаметру некоторого трубопровода круглого сечения, у которого отношение площади поперечного сечения к смоченному периметру то же, что и у данного трубопровода некруглого сечения.

Например:

для канала прямоугольного сечения (рис. 1.25)

,

для канала кольцевого сечения (рис. 1.25)

.

Дифференциальные уравнения движения Эйлера. Рассмотрим установившийся поток идеальной жидкости, которая движется без трения, т. е. не обладает вязкостью. Выделим в потоке элементарный параллелепипед объемом dV = dx dy dz, ориентированный относительно осей координат (см. рис. 1.3).

Проекции сил тяжести и давления, действующих на параллелепипед, составляют:

на ось х

,

на ось у

,

на ось z

.

Согласно основному принципу динамики, сумма проекций сил, действующих на движущийся элементарный объем жидкости, равна произведению массы жидкости на ее ускорение.

Масса жидкости в объеме параллелепипеда равна

. (1.72)

Если жидкость движется со скоростью , то ее ускорение равно , а проекции ускорения на оси координат: , и , где _x, _y и _z — составляющие скорости вдоль осей х, у и z. Для установившегося потока в рассматриваемом случае , и . Производные же , и отвечают изменению во времени значений _x, _y и _z при перемещении частицы жидкости из одной точки пространства в другую. Тогда в соответствии с основным принципом динамики

,

, (1.73)

,

или после сокращения

,

, (1.74)

,

где субстанциональные производные соответствующих составляющих скорости

,

, (1.75)

.

Система уравнений (1.74) с учетом выражений (1.75) представляет собой дифференциальные уравнения движения идеальной жидкости Эйлера для установившегося потока.

При неустановившемся движении скорость жидкости изменяется не только при перемещении частицы потока из одной точки пространства в другую, но и с течением времени в каждой точке. Поэтому для неустановившихся условий они принимают вид

,

, (1.76)

.

Система уравнений (1.74) с учетом выражений (1.76) представляет собой дифференциальные уравнения движения идеальной жидкости Эйлера для неустановившегося потока.

Дифференциальные уравнения движения НавьеСтокса. При движении реальной (вязкой) жидкости в потоке жидкости помимо сил давления и тяжести действуют также силы трения.

Действие сил трения Т на выделенный в потоке вязкой жидкости элементарный параллелепипед (рис. 1.26) проявляется в возникновении на его поверхности касательных напряжений . Рассмотрим первоначально относительно простой случай одномерного плоского потока капельной жидкости в направлении оси х, когда проекция скорости v_x зависит только от расстояния z до горизонтальной плоскости отсчета.

В

Рис. 1.26. Схема к выводу уравнений НавьеСтокса

этих условиях касательные напряжения возникают лишь на поверхностях dF верхней и нижней граней элементарного параллелепипеда, причем dF = dx dy. Если касательное напряжение на нижней грани параллелепипеда равно , то на верхней оно составляет .

Производная выражает изменение касательного напряжения вдоль оси z в точках, лежащих на нижней грани параллелепипеда, а представляет собой изменение этого напряжения вдоль всей длины dz ребра параллелепипеда.

Указанные на Рис. 1.26 стрелками направления сил трения, приложенных к параллелепипеду на его нижней и верхней гранях, обусловлены тем, что более медленные вышележащие слои жидкости затормаживают слой, в котором находится параллелепипед, а более быстрые нижележащие слои «разгоняют» его.

Тогда проекция равнодействующей сил трения на ось х

. (1.77)

Подставив в это выражение значение касательного напряжения из уравнения , где  вязкость жидкости, получим

. (1.78)

В более общем случае трехмерного потока составляющая скорости _x будет изменяться не только в направлении z, но и в направлениях всех трех осей координат. Тогда проекция равнодействующей сил трения на ось х примет вид

.

Сумму вторых производных по осям координат называют оператором Лапласа:

. (1.79)

Следовательно, проекция равнодействующей сил трения на ось х может быть представлена как . Соответственно проекции равнодействующей сил трения:

на ось у

,

на ось z

.

Проекции на оси координат равнодействующей всех сил (тяжести, давления и трения), действующих на элементарный объем капельной жидкости (с учетом проекций сил тяжести и давления, полученных при выводе уравнений Эйлера), составляют:

на ось х

,

на ось y

,

на ось z

.

Суммы проекций сил на оси координат, в соответствии с основным принципом динамики, должны быть равны произведению массы жидкости  dx dy dz (  плотность жидкости), заключенной в элементарном объеме, на проекции ускорения на оси координат. Поэтому, приравнивая проекции равнодействующей произведениям массы на проекции ускорения, после сокращения на dx dy dz, получим

,

, (1.80)

,

где соответствующие субстанциональные производные выражены для установившегося и неустановившегося потоков уравнениями (1.75) или (1.76).

Уравнения (1.80) представляют собой уравнения НавьеСтокcа, описывающие движение вязкой капельной жидкости.

При движении идеальной жидкости, когда силы трения отсутствуют, при подстановке  = 0 в уравнения (1.80) последние совпадают с уравнениями движения Эйлера. Полное описание движения вязкой жидкости возможно путем решения уравнений НавьеСтокса совместно с уравнением неразрывности потока. Однако уравнения НавьеСтокса не могут быть решены в общем виде. Этостановится возможным либо при ряде упрощающих допущений, либо при преобразовании уравнений методами теории подобия.

Распределение скоростей и расход жидкости при установившемся ламинарном потоке. В случае ламинарного движения вязкой жидкости в прямой трубе круглого сечения всю жидкость можно мысленно разбить на ряд кольцевых слоев, соосных с трубой (Рис. 1.27, а).

Рис. 1.27. Схема к определению распределения скоростей и расхода жидкости при