1)Матрицы, линейные операции над ними. Умножение матрицы. Матрица(А)- Матрица размером м*н – совокупность м*н чисел расположенных в виде прямоугольной таблицы из м строк и н столбцов. умножение матриц – A*B, строка матрица А умножается на столбец матрицы В такмм образом получается строка новой матрицы. 2)Определители 2-го и 3-го порядка, их вычисление. Свойства определителей. Теорема разложения Оперделитель 2-ого и 3-его порядка – это определитель считаемый в квадратных матрицах 2х2 и 3х3 Свойства определителей 1. если какая либо строка(столбец) определителя состоит из одних 0,то такой определитель будет равен 0 2. если все элементы строки(столбца) умножить на число λ, то и определитель умножиться на это число λ Следствие: за знак определителя можно выносить общий множитель любой строки или столбца 3. при перестановке двух строк( столбцов) знак определителя меняется на противоположный 4.если определитель содержит две одинаковые строки(столбцы), то определитель равен 0 5. если элементы двух строк(столбцов) пропорциональны, то определитель равен 0 6. определитель не изменится. Если к элементам какой-либо строки(столбца)прибавить соответствующие элементы другой строки(столбца),умноженных на какое-либо число . Алгебраическое дополнение (А ij) элемента а ij называется его минор взятый со знаком (-1)^i+j Aij=(-1)^i+j *Mij Минор (М ij) элемента а ijназывается определитель полученный из данного путем вычеркивания i-строки и j-столбца Теорема разложения: Определитель n-го порядка, n>1, равен сумме произведени элементов любой строки (столбца) на их алгебраические дополнения. 3)Системы линейных алгебраических уравнений. Решение систем 2-х уравнений по способу Крамера. Формулы Крамера для систем и линейных алгебраических уравнений с квадратной матрицей. Метод Крамера: данный метод применяется для систем у которых число уравнений совпадает с числом неизвестных А= -матрица системы Теорема Крамера: пусть определительматрицы системы; а j- определитель матрицы,получаемой из матрицы А,заменой j-столбца столбцом свободных членов тогда 1) если не равно 0,то система имеет единственное решение,которое вычисляется по формуле 2) если =0,то а)если хотя бы одни из определителей отличен от 0,то система не имеет решений; б) если все определители =0,то система имеет бесконечно много решений 4)Векторы. Линейные операции над векторами в геометрической форме: сложение, вычитание, умножение на скаляр. Коллинеарные векторы. Равные и противоположные векторы. Компланарные векторы. Вектор-направленный отрезок, имеющий определенную длину, т.е. это отрезок определенной длины,у которого одна из ограничевающих точек принимается за начало, а другая за конец. Равные векторы:компланарные ,одинаково направленные и имеющие одинаковую длину Противоположные векторы: длины векторов равны, и они противоположно направлены Орт-вектор: единичный вектор (длина=1) сонаправленный с данным а Компланарные векторы: расположенные на прямых параллельных одной и той же плоскости 5 билет: свойства проекций и т.д. 1 проекция ветора на ось = произведению модуля вектора на косинус угла между вектором и осью 2 проекция суммы нескольких векторов на одну ось = сумме их проекций на эту ось 3 при умножение вектора на число его проекция так же умножается на это число модуль вектора = квадратному корню из суммы квадратов его проекций на оси координат косинус альфа , бета, гамма – направляющие косинусы( между осью х у z ) разложение по ортам – a_x*i+ a_y*j+ a_z*k векторы имеющие пропорциональные координаты коллиниарны Координаты вектора = разностям соответсвующих координат его начала и конца 6)Скалярное произведение двух векторов, его свойства. Вычисление скалярного произведения и его применение. Условие перпендикулярности векторов. Скалярное произведение двух векторов-число равное произведению длин этих векторов на cos между ними

С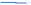 войства скалярного произведения: 1. комутативность 2.для любого числа λ и любых векторов а и bвыполняется равенство 3. для любых векторов а,b,c выполняется равенство 4.для любого вектора а будет выполнятся равенство 5.скалярное произведение равно 0,тогда и только тогда, когда векторы перпендикулярны Скалярное произведение в координатах-равно сумме произведений соответствующих координат Применение: 1. вычисление угла между векторами 2. установление факта перпендикулярности векторов 2. нахождение проекции одного вектора над другой 3.вычисление работы постоянной силы A=FS(S= )

7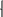 )Векторное произведение двух векторов, его свойства. Вычисление векторного произведения и его применение. Векторное произведение векторов а и bназывается вектор с= = ,обладающий 3 свойствами: 1. вектор с , с 2. -образуют правую тройку векторов 3. правило параллелограмма Свойства векторного произведения: 1. = 2. 3. 4. 5. Вычисление векторного произведения: Применение: 1.вычисление площади парал-ма, построенного на векторах 2. 3.вычисление момента силы 8)Смешанное произведение трех векторов, его геометрический смысл. Свойства смешанного произведения, его вычисление и применение. Смешанное произведение векторов а,b,c-число равное скалярному произведениюа на вектор равный векторному произведению bна с Свойства смешанного произведения: 1. смешанное произведение равно 0 а) если хотя бы один из векторов равен 0 б)если два вектора компланарны в)если все векторы компланарны 2. При циклической (круговой) перестановке множителей смешанное произведение не изменяется При перестановке двух множителей смешанное произведение изменяет знак на противоположный , , 3. 4. Вычисление смешанного произведения: Применение: 1. , 2. -компланарны, если смешанное произведение равно 0 3.точки А,В,С,D лежат в одной плоскости, если векторы АВ, АС, АD- компланарные, т.е. смешанное произведение равно 0 9)Прямая на плоскости. Общее уравнение прямой. Уравнение прямой с угловым коэффициентом. Угол между прямыми на плоскости. Условия параллельности и перпендикулярности прямых на плоскости. Уравнения прямой, проходящей через одну или две заданные точки на плоскости. Расстояние от точки до прямой. Ax + By + C=0-общее уравнение прямой(уравнение первой степени относ-но XY); А,В,С –производные числа причем А и В не равны 0(одновременно) y=kx+b-уравнение прямой с угловым коэффициентом угол между прямыми на плоскости Условия параллельности двух прямых :k1 = k2 Условия перпендикулярности двух прямых:k1k2= - 1 Уравнения прямой, проходящей через одну или две заданные точки на плоскости: 1. Уравнение прямой, проходящей через данную точку A(x1, y1) в данном направлении, определяемом угловым коэффициентом k, y - y1 = k(x - x1) 2. Уравнение прямой, проходящей через две точки: A(x1, y1) и B(x2, y2), записывается так: Расстояние от точки до прямой : Расстояние точки A(x1, y1) до прямой Ax + By + C = 0 есть длина перпендикуляра, опущенного из этой точки на прямую 10)Кривые второго порядка: эллипс, гипербола, парабола. Канонические уравнения. Уравнения с центром в точке(α;β). Эллипс- геометрическое место точек сумма расстояний от которых до двух данных точек называемых фокусами есть величина постоянная a > b, то с2=а2-b2; а <b, то с2=b2-а2 Гипербола- геометрическое место точек разность расстояний от которых до двух данных точек называемых фокусами есть величина постоянная а) с2=а2+b2(ветви по бокам); б) (ветви сверху и снизу) асимптота-такая прямая,что расстояние от точки на кривой до этой прямой стремится к нулю при неограниченном удалении точки на кривой от начала координат а)у=+-(b/а)х б)у=+-(а/b)х Парабола-геометрическое место точек равноудаленных от данной точки называемой фокусом и данной прямой называемой дириктрисой 1) x^2=2py;y=p/2 (график наверху) 2) x^2=-2py;y=p/2 (график внизу) 3)y^2=2px; х=-p/2 (график справа) 3) y^2=-2px; x=p/2 (график слева) Канонические уравнения: 1) эллипс 2) парабола 3)гипербола Уравнения с центром в точке 0(х 0; у 0): 1.эллипс (х-х 0)^2/a^2 +(y-y 0)^2/b^2=1 2.гипербола а) (х-х 0)^2/a^2 - (y-y 0)^2/b^2=1б)(х-х 0)^2/a^2 - (y-y 0)^2/b^2=- 1 3. парабола (х-х 0)^2=+-2p(y-y 0); (y-y 0)^2=+- 2p(х-х 0) 11)Плоскость в пространстве.Взаимное расположение плоскостей.Расстояние от точки до плоскости.

-Общее уравнение пл-ти: Ax+By+Cz+D=0 где (x,y,z)- координаты пл-ти

-Ур-е пл-ти,проходящей через 3 данных точки Пусть М₁(x₁;y₁;z₁),M₂(x₂;y₂;z₂) и М₃(x₃;y₃;z₃) лежат в 1 пл-ти.Пусть М-произвольная точка пл-ти.Тогдакоорд. векторов М₁М=(х-х₁;y-y₁;z-z₁), M₁M₂=(x₂-x₁;y₂-y₁;z₂-z₁) и М₁М₃=(x₃-x₁;y₃-y₁;z₃-z₁) Точки М,М₁,М₂,М₃-лежат в 1 пл-ти,если Вектора М₁М,М₁М₂,М₁М₃-компланарны.Следует,что смешаное произведение =0 М₁М*М₁М₂*М₁М₃=0 Условие параллельности 2 плоскостей.

Две плоскости α₁ и α₂ параллельны тогда и только тогда, когда их нормальные векторы   и   параллельны, а значит .

-Условие перпендикулярности 2 пл-тей

две плоскости перпендикулярны тогда и только тогда, когда их нормальные векторы перпендикулярны, а следовательно,  или 

-Расстояние от точки до пл-ти :Расстояние от произвольной точки М₀(х₀, у₀, z₀)  до плоскостиАх+Ву+Сz+D=0 равно:

12)Прямая в пространстве.Общие,параметрические и канонические уравнения прямой в пространстве.Взаимное расположение прямых в пространстве.Точка пересечения прямой и плоскости в пространстве.Взаимное расположение прямой и плоскости в пространстве.

 -Прямая, являющаяся линией пересечения 2 плоскостей, задается системой уравнений:

Положение прямой в пространстве определено,если задана точка М₀ на прямой и вектор S параллельный этой прямой(лежащий на этой прямой)S-направляющий вектор прямой.ПустьS={m,n,p)Векторное ур-е прямой:r=r₀+t*S,где S,r,r₀-векторы.

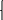- Параметрическое ур-е прямой: r={x,y,z}, r₀={x₀,y₀,z₀}, t*S={t_m,t_n,t_p}, то ур-е: х=х₀+mt

Y =y₀+nt y=y₀+tn

Z=z₀+pt -каноническое уравнение прямой в пространстве -Ур-е прямой проходящей через 2 точки:х-х₁\х₂-х₁=y-y₁\y₂-y₁=z-z₁\z₂-z₁

-Условие парал-ти 2 прямых: S₂ ||S ,то m₁\m₂=n₁\n₂=p₁\p₂

-Условие перпендикулярности 2 прямых: S₁_|_S₂,еслиS₁*S₂=0 Прямая и плоскость в пространстве могут: а) не иметь общих точек; б) иметь ровно одну общую точку; в) иметь хотя бы две общие точки. Точка пересечения прямой и плоскости 13)Переменная.Функция ,область ее определения.Способы задания функции.Важнейшие свойства функции:четность,нечетность,периодичность,наличие обратной функции.Классификация.

Если к каждому значению х из множества Х поставлено в соответствии по определенному правилу f единственное значение переменной y из множества Y,то говорят,что задана функция y=f(x), определенная на множ-ве Х с областью значения Y.

х-аргумент,y-функция.Х-ООФ,Y-ОЗФ.

С пособы задания функции:1)Табличный(используется если множество Х конечно) 2)Графический (Графиком функции y=f(x) называется множество точек с координатами (x,y), где х принадлежит Х,yпринад. Y) 3)Аналитический: а)в явном виде(y=f(x)) б) в неявном виде (F(x,y)=0)пример: х²+y²=4 в)параметрическизаданнаx=x(t) y=y(t) Функция y=f(x), область определения которой симметрична относительно начала координат называется четной, если y(-x)=y(x) Нечетной,еслиy(-x)=-y(x).

Функция y=f(x) называется периодической,еслисуществуетчислоТ,такое что f(x+T)=f(x)

Пусть дана ф-я y=f(x),где х ϵ Х, yϵY,если любому значению yϵY ставиться соответ. значение х ϵ Х,такое что y=f^-1(x),то говорят что задана функция х=y(f) ,которую называют обратной.

Отображение y=f(x) называется взаимооднозначным,если разным значениям х соответствуют разные значения y.

Классификация ф-ий: 1)Элементарные а)степенные б)показательные в)тригонометрические (y=sinx) г)обратные тригонометрическим д)логарифмические.Элементарныеделяться на:1)алгебраические а)многочлен. б)рациональная дробь в)ирроциональная г)модуль перемен. 2)Трансцедентные а)логарифмич. б)показат. в)тригонометр. – гипорболическийсинус,косинус, тангенс и катангенс.

14)Предел функции при х ->а и при х->∞.Геометрическая интерпритация предела функции.Односторонние пределы.

Пусть ф-я y=f(x) определена на некотором множестве Х,а-фиксированная точка на оси ОХ.Точка а может принадлежать, не принадлежать оси ОХ.Дельта окрестностью точки а называют интервал |х-а|<δ,где δ-окрестность(U_a). Пусть ф-я y=f(x) определена на некотором множестве Х,а-фиксированная точка на оси ОХ,число В называется пределом ф-и y=f(x) в точке а или при х->а. Если для любого числа ε>0 существует такое число,зависящее от δ,что для всех х удовлетвор.неравенству 0<|х-а|<δ выполняется неравенство f(x)=B<ε.Определение означает,что если lim f(x)=B,то всегда найдется дельта-окрестность такая,что значения ф-и для х из этой окретности сколь угодно мало отличное от В.

Число В называется пределом ф-и y=f(x) при х->∞,если для любого ε>0 существует такое число δ зависящее от ε>0,что при всех х удовлетворяющих неравенству |х|>δ,выполняется неравенство |f(x)-B|<ε.

Предел слева от точки х=а , справа.

15)Бесконечно большие и бесконечно малые функции.Ихсвойства.Примеры.

Функция называется ограниченной при х стремящимся к а ,если существует такая окрестность и такое число М>0,что |f(x)|<M для любых х из этой окрестности. Ф-я y=f(x) называется бесконечно большой при х->а,если для любого числа ε>0 существет δ зависящая от ε,такое что для всех х удовлетворяющих неравенству 0<|x-a|<δ следует |f(x)|>ε. F(x)-бесконечно большая при х->а,если сущ-ет окрестность точки а во всех точках которой значение ф-и по модулю больше сколь угодного числа ε.( limf(x)=∞,при х->а)

Если y=f(x) имеет конечный предел при х->а,то ф-я является ограниченной в некоторой окрестности а.

Ф-я y=α(x) называется бесконечно малой при х->а если для любого числа ε>0 существует δ зависящее от ε,такое что для всех х удовл.неравенству0<|x-a|<δ следует,что |α(x)|<ε.( lim α(x)=0,при х->а).

Свойства:1)б.м.±бм=бм 2)бм*бм=бм 3)бм*огр=бм 4)огр\бм=бб 5) бб±бб=бб 6)бб*бб=бб 7)бб*огр=бб(огр≠0) 8)огр\бб=бм

Всёостальное дает неопределенности (∞-∞),(0\0) и т.д. 16)Теоремы о конечных пределах.

1)Основная теорема о конечных пределах:Для существования конечного пердела limf(x) при х->а f(x)=B,необходимо чтобы y=f(x) можно было представить в виде суммы б.м. велечин (f(x=B+α(x))).

2)Предел суммы и разности ф-и: Если limf(x) при х->а=A и limg(x) прих->а=B,где А и В-числа,тоlim(f(x)±g(x))=A±B

3)Предел произведения: Если lim f(x) при х->а=Aи lim g(x) при х->а=B,где А и В-числа,тоlim(f(x)*g(x))=A*B.Следствие: постоянный множитель можно вынести за знак предела.

4)Предел отношения 2 ф-ий: Если lim f(x) при х->а=A и lim g(x) при х->а=B,где А и В-числа, В≠0, то lim(f(x)\g(x))=A\B

5)О предельном переходе в неравенствах: Если в некоторой окрестности а, выполняется условие f(x)≤g(x) исуществуют пределы lim f(x) при х->а=A и lim g(x) при х->а=B, и конечные пределы,тоЕсли lim f(x) при х->а≤lim g(x) при х->ат.е А≤В

Следствие:Еслиy=f(x)>0 и lim f(x) при х->а=A, то lim f(x) при х->а≥0 т.е. А≥0

6)Теорема о промежуточной ф-и: Если в некоторой окрестности точки а выполняется условие f(x)≤u(x)≤g(x) и существует предел lim f(x) при х->а=A и lim g(x) при х->а=B, то существует предел limu(x) при х->а.

1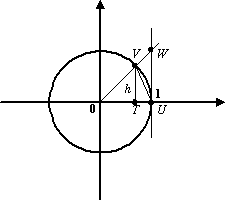 7)Первый и второй замечательные пределы .Число е. 1зам.предел)Доказательство:отложим на тригонометрическом круге угол α.считаем что 0<α<π\2. Достроем хорду VU, WU перпендикулярно 0U, VTперпенд. 0U. S_0VT-самая маленькая,S_0VU-средняя, S_0WU-большая.S_сек=1\2*R²*α.S_0VU=1\2VT*0U, Sсек=1\20U²*x , S_OWU=\2 0U*WU , следует VT<x<WUsinx<x<tgx(разделим на синус х),

1<x\sinx<1\cosx,перейдем к обратным велечинам 1>sinx\x>cosx , cosx<sinx\x<1.Перейдем к пределу: limcosxприx->0+0 <limsinx\xпри x->0+0<lim 1 при х->0+0. 1<lim при х->0+0<1. х->0+0-стремиться к 1,тогда limsinx\x при x->0+0=1.

2зам.предел) е=2.71

18)Сравнение бесконечно малых функций.Эквивалентно бесконечно малые.Принцип замены эквивалентно бесконечно малых и его использование при вычислении пределов.

1) Если limα(x)\ß(x) =1 то назыв.эквивалентными бесконечно малыми α(x)~ß(x)

2)Если limα(x)\ß(x) при х->а =c≠0 тоα(x) и ß(x) называются бесконечно малыми одного порядка малости.

3)Если lim α(x)\ ß(x) при х->а =0 то α(x) имеет более высокий порядок малости

4)Если lim α(x)\ ß(x) при х->а =∞ то ß(x) имеет более высокий порядок малости

5)Если lim α(x)\ ß(x) при х->а не существует ,то сравнить нельзя

Теорема(принцип замены эквивалентных): Если α(х) и ß(х) два эквивалентных бесконечно малых при х->а и f(х)-функция определенная в некоторой окрестности точки а,тоlim α(х)*f(х)при х->а = lim ß(х) *f(х) при х->а

Замечание:домножить на эквивалентные можно только бесконечно малый сомножитель,но не слагаемое.