14. Геометрический смысл смешанного произведения (док-во).

Th.Смешанное произведение трех векторов равно объему параллелепипеда, построенного на этих векторах. Док-во: Построим параллелепипед, ребрами которого являются векторы а͞ , b͞ , с͞ и вектор d͞ =[а͞ ,b͞ ] ([а , ͞b] , ͞с )=( ͞d,͞с) = |d| • при с, |d|=|а * b| =S, где S — площадь параллелограмма, построенного на векторах а и b, при с = Н Для правой тройки векторов и пр_dс = - Н для левой, где Н— высота параллепипе­да. Получаем: (a*b )*c =S *(±H ), т. е. ([͞a,͞b ]*͞c) =±V , где V — объем параллепипеда, образованного ͞а, ͞b и ͞с.

Т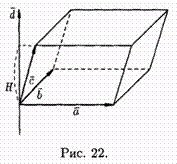 . о., смешанное произведение трех векторов равно объему параллепипеда, построенного на этих векторах, взятому со знаком «плюс», если эти векторы образуют правую тройку, и со знаком «минус», если образуют левую тройку.

15. Вывод координатного ( ( ) ), векторного( ) и параметрических ( ) уравнений прямой на плоскости.

Получим координатную форму записи векторного уравнения прямой . Так как   , по формуле находим   или Полученное соотношение позволяет по координатам точки   и координатам A,B нормали n записать уравнение прямой без промежуточных вычислений. Обозначив  , получим уравнение

Векторное уравнение прямой. Описание прямой в пространстве при помощи общих уравнений — не единственный способ. Прямую L в пространстве можно также однозначно задать любой ее точкой M0 и параллельным ей ненулевым вектором s. Любой ненулевой вектор, параллельный прямой, называют направляющим вектором прямой.

Если точка M принадлежит прямой L, то это эквивалентно тому, что вектор коллинеарен вектору s. Так как s 0, то вектор s является базисом в пространстве

коллинеарных ему векторов. Поэтому для некоторого числа t выполняется равенство

= ts. Так как , где r и — радиус-векторы точек M и

соответственно, то условие M ∈ L можно записать в виде уравнения которое называют векторным уравнением прямой в пространстве.

Векторно-параметрическое уравнение прямой задается вектором   конец которого лежит на прямой, и направляющим вектором прямой a. Параметр t пробегает все действительные значения.

Параметрические уравнения прямой

Предположим, что известны координаты {l;m; n} направляющего вектора s прямой L и точки ∈ L в прямоугольной системе координат. Обозначим через (x; y; z) координаты произвольной точки M.

Критерием принадлежности точки M прямой L является условие коллинеарности векторов , что равносильно пропорциональности их координат. Обозначив через t коэффициент пропорциональности, получим равенства . Но тогда 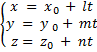и называют параметрическими уравнениями прямой в пространстве. Шесть коэффициентов в системе уравнений имеют наглядный геометрический смысл: они представляют собой координаты одной точки на прямой, соответствующей t = 0, и координаты направляющего вектора прямой, который соединяет точки, соответствующие значениям параметра t = 0 и t = 1.

Итак, если задана система трех уравнений вида (6.3), в которой хотя бы один из коэффициентов отличен от нуля, то эта система определяет в пространстве прямую, причем тройка коэффициенто задает на прямой точку, а тройка коэффициентов представляет собой координаты направляющего вектора прямой.

Параметрические уравнения прямой могут быть записаны в виде:

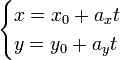
где t — производный параметр, a_x, a_y — координаты x и y направляющего вектора прямой, при этом

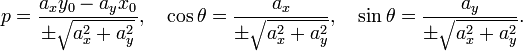
Смысл параметра t аналогичен параметру в векторно-параметрическом уравнении.