
Билет № 9. Равновесие твердого тела, имеющего неподвижную ось. Возможность переноса точки приложения силы. Момент силы относительно оси.
Равновесие твердого тела, имеющего неподвижную ось
Следует отметить, что при вращательном движении тело обретает устойчивость, например, монета может катиться на ребре и не падать. Анализируя результаты опытов, можно прийти к следующему выводу: тело, вращающееся вокруг оси, проходящей через центр масс, должно сохранять вращение неопределенно долго при освобождении от внешних воздействий. Это заключение аналогично первому закону Ньютона для поступательного движения.
 Внешнее
воздействие изменяют состояние движения.
Рассмотрим схему следующего опыта.
Крестовина насажена на ось со шкивом,
радиус шкива можно менять. Можно также
изменять расстояние от оси вращения до
грузов массой М.
Гиря массой m привязана к нити, нить
перекинута через неподвижный блок и
соединена со шкивом. На данной установке
можно наблюдать следующее: если масса
гири не изменяется (т.е. приложенная к
крестовине сила постоянна), то ускорение
крестовины зависит : а) от положения
грузов – если грузы удалять от оси
вращения, то ускорение уменьшается, б)
от радиуса шкива – чем больше радиус,
тем больше ускорение.
Внешнее
воздействие изменяют состояние движения.
Рассмотрим схему следующего опыта.
Крестовина насажена на ось со шкивом,
радиус шкива можно менять. Можно также
изменять расстояние от оси вращения до
грузов массой М.
Гиря массой m привязана к нити, нить
перекинута через неподвижный блок и
соединена со шкивом. На данной установке
можно наблюдать следующее: если масса
гири не изменяется (т.е. приложенная к
крестовине сила постоянна), то ускорение
крестовины зависит : а) от положения
грузов – если грузы удалять от оси
вращения, то ускорение уменьшается, б)
от радиуса шкива – чем больше радиус,
тем больше ускорение.
Отдельные элементы вращающегося тела с массами dmi находятся на расстоянии ri от оси вращения и движутся с различными линейными скоростями vi, но угловая скорость ω у всех элементов одинакова.
Вычислим полную кинетическую энергию вращающегося тела:

 (1).
(1).
Величина
I
=![]() ri2mi (2)
– величина зависящая от распределения
масс относительно оси вращения, называется
моментом инерции тела относительно
данной оси. Она равна арифметической
сумме элементарных моментов инерции
относительно той же оси, т.е. по-другому
можно записать I=Σri2mi (3).
Размерность момента инерции [ I
] = кг · м2.
ri2mi (2)
– величина зависящая от распределения
масс относительно оси вращения, называется
моментом инерции тела относительно
данной оси. Она равна арифметической
сумме элементарных моментов инерции
относительно той же оси, т.е. по-другому
можно записать I=Σri2mi (3).
Размерность момента инерции [ I
] = кг · м2.
Число осей вращения для каждого тела неопределенно велико, столь же много существует и моментов инерции (ни один из них е может равняться нулю, так как все элементарные моменты ri2mi положительны). Моменты осей, проходящие через центр масс, называются главными моментами инерции, они находятся методами интегрального исчисления, основные из них следующие:
а ) для
тонкостенного кругового цилиндра
(диска) относительно оси ОО момент
инерции I0=MR2 (4);
) для
тонкостенного кругового цилиндра
(диска) относительно оси ОО момент
инерции I0=MR2 (4);
б) для
сплошного кругового цилиндра (диска)
относительно оси ОО момент инерции
![]() (5);
(5);
в) для
любого цилиндра (диска), если ось вращения
АА проходит через центр масс перпендикулярно
оси цилиндра момент инерции
![]() (6).
(6).
Для
шара момент инерции относительно любого
диаметра
![]() (7),
где R – радиус шара, M – масса шара.
(7),
где R – радиус шара, M – масса шара.
Если ось вращения не проходит через центр масс, то момент инерции I относительно этой оси можно вычислить по формуле
I = I0 + Ma2 (8),
где а – расстояние от центра масс до оси вращения. Соотношение (8) называют теоремой Штейнера.
П усть
тело произвольной формы имеет ось
вращения О (расположенную перпендикулярно
плоскости чертежа), и на тело действует
сила
усть
тело произвольной формы имеет ось
вращения О (расположенную перпендикулярно
плоскости чертежа), и на тело действует
сила
![]() в
плоскости, перпендикулярной оси. Проведем
от оси до точки приложения силы радиус
вектор R и разложим силу F на две
составляющие:
в
плоскости, перпендикулярной оси. Проведем
от оси до точки приложения силы радиус
вектор R и разложим силу F на две
составляющие:
![]() ,
действующую параллельно радиус-вектору,
и
,
действующую параллельно радиус-вектору,
и
![]() перпендикулярную
к нему. Сила
изгибает
ось, но не создает вращения. Мы пренебрежем
деформацией и далее не будем рассматривать
эту составляющую. Модуль силы
,
как видно из рисунка, равен F2=Fsinα.
Сила F2
будет создавать вращение и сообщать
телу угловое ускорение
перпендикулярную
к нему. Сила
изгибает
ось, но не создает вращения. Мы пренебрежем
деформацией и далее не будем рассматривать
эту составляющую. Модуль силы
,
как видно из рисунка, равен F2=Fsinα.
Сила F2
будет создавать вращение и сообщать
телу угловое ускорение
![]() .
Если взять малое перемещение dS
=r·dφ , где dφ
- угловое перемещение, то сила F2
совершит элементарную работу
.
Если взять малое перемещение dS
=r·dφ , где dφ
- угловое перемещение, то сила F2
совершит элементарную работу
dA = F2dS = F2 R dφ= [dφ = ωdt] = FR ω dt (9).
Но работа равна изменению кинетической энергии, т.е.
FR
ω dt =
![]() =
Iωdω.
=
Iωdω.
![]() .
.
Согласно определению F·R = M (момент силы) , следовательно,
M = I· ε (10).
Это
основное уравнение динамики вращательного
движения. Сравнивая его с уравнением
![]() ,
видим, что момент инерции играет роль
массы при вращательном движении: чем
больше момент инерции I, тем меньше
угловое ускорение ε.
,
видим, что момент инерции играет роль
массы при вращательном движении: чем
больше момент инерции I, тем меньше
угловое ускорение ε.
Для материальной точки, введя импульс, мы получали соответственно
![]() (11).
(11).
Аналогично для вращающегося тела можно вывести уравнение
![]() (12),
(12),
показывающее,
момент внешних сил изменяет момент
механического импульса во времени.
Величина
![]() (13)
называется моментом механического
импульса.
(13)
называется моментом механического
импульса.
Итак, можно провести аналогию между поступательным и вращательным движением.
Сравнительные параметры движения:
Поступательное движение |
Вращательное движение |
Перемещение S |
Угловое перемещение φ |
Линейная скорость v |
Угловая скорость ω |
Ускорение a |
Угловое ускорение ε |
Масса m |
Момент инерции I |
Сила F |
Момент силы M |
Импульс p |
Момент импульса L |
В замкнутой системе момент внешних сил отсутствует. Из уравнения (12) следует, что
![]() =const (14).
=const (14).
Это важное соотношение выражает третий закон сохранения в механике – закон сохранения момента механического импульса.
Закон
сохранения момента импульса можно
проверить с помощью скамьи Жуковского
(диск, который может вращаться без
заметного трения вокруг вертикальной
оси). Экспериментатору сообщают известный
момент механического импульса
![]() ,
где I1
– момент инерции экспериментатора
вместе со скамейкой и грузами. Если он
прижимает руки к туловищу, то за счет
действия внутренних сил момент инерции
уменьшается. В
,
где I1
– момент инерции экспериментатора
вместе со скамейкой и грузами. Если он
прижимает руки к туловищу, то за счет
действия внутренних сил момент инерции
уменьшается. В нутренние
силы не могут изменить момент импульса,
следовательно, для его сохранения
скорость вращения ω2
должна возрасти. Таким образом
нутренние
силы не могут изменить момент импульса,
следовательно, для его сохранения
скорость вращения ω2
должна возрасти. Таким образом
I1ω1 = I2ω2.
Закон сохранения момента механического импульса выполняется и для случая произвольного вращения в замкнутой системе (т.е. не только в том случае, когда ось вращения неподвижна).
Рассмотрим частный случай вращательного движения – рычаг. Рычагом называется твердое тело, имеющее неподвижную ось вращения и подверженное действию не менее двух моментов внешних сил. Рычаг находится в равновесии в случае, когда моменты сил равны и направлены в разные стороны, т.е. М1 = М2 или F1a = F2b.
Обобщая условия равновесия рычага, можно уточнить условия движения свободного твердого тела в частном случае, когда все действующие на него внешние силы лежат в одной плоскости.
Е сли
сумма сил отлична от нуля и ее
равнодействующая проходит через центр
масс, то тело движется поступательно.
Если сумма моментов сил относительно
центра масс не равна нулю, то тело
приходит во вращательное движение.
сли
сумма сил отлична от нуля и ее
равнодействующая проходит через центр
масс, то тело движется поступательно.
Если сумма моментов сил относительно
центра масс не равна нулю, то тело
приходит во вращательное движение.
Таким образом, тело будет находиться в равновесии, если сумма моментов действующих на него сил равна нулю.
Различают следующие виды равновесия; если тело сместить немного из положения равновесия и предоставить самому себе, то:
а) оно может самопроизвольно возвратится в положение равновесия (устойчивое равновесие);
б) остаться в новом положении (безразличное равновесие);
в) отходит от положения равновесия (неустойчивое равновесие).
Возможность переноса точки приложения силы
В § 35 мы видели, что равные силы, действующие вдоль одной прямой в противоположные стороны, уравновешивают друг друга. При этом несущественно, к какой именно точке тела на этой прямой приложены силы. Так, на рис. 97 показаны два случая приложения к телу равных и противоположных сил f1 и f2, действующих вдоль одной прямой. Оба случая различаются только точкой приложения силы f1 (А или А’); в обоих случаях тело остается в равновесии. Таким образом, в случае равновесия двух сил точку приложения силы можно переносить вдоль ее направления, не нарушая равновесия тела. Опыты показывают, что такой перенос не меняет действия силы и в других случаях действия сил на твердое тело. Например, одна сила, приложенная к телу, вызовет одно и то же ускорение тела как целого, где бы ее ни приложить. Точку приложения силы можно переносить вдоль ее направления, не меняя действия силы на тело в целом. Мы можем не только в действительности переносить точки приложения сил, но можем производить эту операцию и мысленно для того, чтобы упростить рассуждения при решении тех или иных задач. Этим приемом часто пользуются как для определения условий равновесия, так и при изучении движений твердого тела. Хотя перенос точек приложения сил не меняет их действия на тело в целом, такой перенос изменяет распределение деформаций и сил упругости в реальном теле. В самом деле, в рассматриваемом примере, когда силы приложены к точкам А и В, они вызывают деформацию тела: в области между точками А и В, возникает растяжение и появляются силы упругости f3 и f4, которые действуют между частями тела, уравновешивая приложенные извне силы f1 и f2, и прекращают дальнейшие деформации. Если же сила f1 приложена в точке A’, то растяжение захватывает уже область от точки А’ до точки В. Однако в обоих случаях упругие силы f3 и f4 возникают уже при ничтожных деформациях, а так как мы не обращаем внимания на деформацию (рассматриваем тело как абсолютно твердое), то различие в деформациях роли не играет.
|
Момент сил относительно оси.
Рассмотрим силу
![]() и точку О, не лежащую на линии действия
силы (рис. 1).
и точку О, не лежащую на линии действия
силы (рис. 1).
Из точки О опустим перпендикуляр на линию действия силы.
Длина этого перпендикуляра h называется плечом силы относительно точки О. Очевидно сила вызовет вращение тела относительно точки О. Вращательный эффект действия силы на тело можно определить как алгебраический момент силы относительно точки
![]() .
(1)
.
(1)
Момент силы F считается положительным, если сила стремится повернуть плоскость, в которой она лежит, против направления движения часовой стрелки вокруг оси, перпендикулярной этой плоскости и проходящей через точку О.

Рис. 1 Момент силы относительно оси
Вращательный эффект действия силы на тело относительно оси определяется моментом силы относительно оси.
Момент силы относительно оси находится иначе, чем момент силы относительно точки.
Алгебраический момент силы относительно некоторой оси равен алгебраическому моменту проекции силы на плоскость, перпендикулярную оси, относительно точки пересечения плоскости с осью (рис. 2).
Правило нахождения момента относительно оси:
Необходимо спроецировать силу на плоскость перпендикулярную оси z.
Подсчитать
момент проекции силы
![]() относительно
точки пересечения оси с плоскостью
относительно
точки пересечения оси с плоскостью
![]() .
(2)
.
(2)
Момент силы относительно оси считается положительным, если при взгляде с положительного направления оси проекция силы стремится повернуть тело против часовой стрелки.
Аксиома: сила, параллельная оси, и сила пересекающая ось, не создают вращения относительно этой оси, то есть моменты таких сил относительно оси равны нулю.

Р ис.
2 Пара сил. Момент пары сил на плоскости
ис.
2 Пара сил. Момент пары сил на плоскости
Парой сил
называется система двух сил
и
![]() (рис.
3), приложенных к твердому телу,
удовлетворяющая следующим условиям:
(рис.
3), приложенных к твердому телу,
удовлетворяющая следующим условиям:
Линии действия сил параллельны.
Модули сил равны (F = F’).
Направления действия сил противоположны.

Плоскость, на которой лежат линии действия пары сил, называется плоскостью действия пары. Расстояние h между линиями действия сил и называется плечом пары. Совокупность пар, приложенных к телу, называется системой пар.
Пара сил, приложенная к телу, стремится сообщить ему некоторое вращение. Вращательный эффект пары характеризуется ее моментом. Моментом пары сил называется произведение модуля одной из сил пары на ее плечо, взятое со знаком «+» или «»
![]() .
(3)
.
(3)
Момент пары считается положительным, когда пара стремится повернуть тело против хода часовой стрелки, и отрицательным - когда по ходу часовой стрелки.
Теорема об эквивалентных парах. Две пары сил, лежащие на одной плоскости и имеющие равные алгебраические величины моментов, эквивалентны.
Доказательство:
Пусть (
,
)
и (![]() ,
,
![]() )
– две пары сил, лежащие в одной плоскости
и имеющие равные моменты М(
,
)
=М(
,
).
)
– две пары сил, лежащие в одной плоскости
и имеющие равные моменты М(
,
)
=М(
,
).

Продолжим линии
действия сил пересечения друг с другом
(рис. 4). Перенесем силы
и
по линиям действия в точки А и В и разложим
каждую из них на составляющие. Получим:
{
,
}
{![]() ,
,
![]() ,
,
![]() ,
,
![]() }.
Из построения имеем
=-
,
=-
,
так как
и
направлены по одной прямой, то {
,
}.
0, а {
,
}
{
,
}.
}.
Из построения имеем
=-
,
=-
,
так как
и
направлены по одной прямой, то {
,
}.
0, а {
,
}
{
,
}.
Докажем
эквивалентность пар (
,
)
и (
,
).
Для этого достаточно доказать, что
=![]() .
.
Плечи пар (
,
)
и (
,
)
равны; момент пары (![]() ,
,
![]() )
численно равен удвоенной площади
треугольника АВС, а момент пары (
,
)
– удвоенной площади треугольника АВD.
)
численно равен удвоенной площади
треугольника АВС, а момент пары (
,
)
– удвоенной площади треугольника АВD.
Но площади этих треугольников равны, так как у них общее основание и равные высоты, опущенные из вершин С и D, то есть F2h=F1h1, но так как Fh=F1h1, то F2h=Fh, следовательно, = , тогда ( , ) ( , ) и ( , ) ( , ).
Следствия из теоремы об эквивалентных парах:
Пару сил можно переносить в любое место плоскости ее действия.
Действие пары сил на тело не изменится, если изменить значения модуля силы и плеча, оставляя величину момента прежней.
Пару сил можно переносить в плоскость, параллельную плоскости действия.
Теорема о сложении пар сил. Пары сил, лежащие в одной плоскости можно складывать.
В результате сложения получается лежащая на той же плоскости пара сил с моментом, равным алгебраической сумме моментов слагаемых пар.
Доказательство:
Докажем для двух пар. Пусть ( , ) и ( , ) – пары, лежащие на одной плоскости и имеющие моменты М1= F1h1 и М2= F2h2.
Возьмем произвольный отрезок АВ=h (рис. 5).
На основании
теоремы об эквивалентных парах можно
заменить введенные пары эквивалентными
им парами (
,
)
и (![]() ,
,
![]() ),
имеющими плечо h.
),
имеющими плечо h.
![]() .
.
Сложив силы в точке А, получим = + ; в точке В –
![]() =
+
;
=-
.
=
+
;
=-
.
![]() .
.
Справедливо для любого числа пар:
![]() .
(4)
.
(4)

Рис. 5 Равновесие рычага
Рычагом называется твердое тело, вращающееся вокруг неподвижной оси и находящееся под действием сил, лежащих в плоскости перпендикулярной к этой оси.
Если на рычаг действует сходящаяся система сил, то равновесие рычага достигается, когда линия действия равнодействующей проходит через точку О (рис. 6), а алгебраическая сумма моментов приложенных к нему сил относительно точки О равна нулю:
 (5)
(5)
Рассмотрим случай, когда на рычаг действует система параллельных сил, лежащих в одной плоскости. Приложенная к рычагу система параллельных сил может быть приведена или к одной равнодействующей, или к паре.
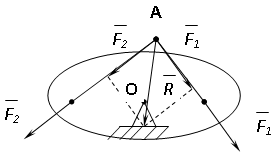
Рис. 6
Сложим все силы, направленные вверх:
![]() ,
,
и вниз:
![]() ,
,
соответственно. Найти точки приложения равнодействующих можно по формулам
 (6)
(6)
В итоге возможны три случая:
1)
![]() ,
тогда система сводится к одной
равнодействующей.
,
тогда система сводится к одной
равнодействующей.
2)
![]() - система не имеет равнодействующей и
сводится к паре сил.
- система не имеет равнодействующей и
сводится к паре сил.
3) , и они направлены по одной прямой, тогда система представляет собой уравновешенную систему сил.

Если система параллельных сил, приложенная к рычагу, сводится к паре, то равновесия рычага быть не может, так как реакция шарнира О (рис. 7) не может уравновесить пару. То есть, при равновесии рычага приложенная к нему система параллельных сил приводится к равнодействующей силе, проходящей через неподвижную точку рычага.
Произвольная плоская система сил Лемма Пуансо.
Действие силы на твердое тело не изменится, если перенести эту силу параллельно своему первоначальному положению в любую точку тела, приложив при этом к телу пару с моментом, равным моменту исходной силы относительно этой точки.
Доказательство:
Пусть сила
приложена к телу в некоторой его точке
А (рис. 8). Приложим в произвольной точке
О параллельно направлению линии действия
силы
две силы
и
![]() ,
равные по модулю силе
и направленные в противоположные
стороны.
,
равные по модулю силе
и направленные в противоположные
стороны.
Полученная система сил { , , } .
Эту систему сил можно считать состоящей из силы , полученной параллельным переносом силы в точку О, и пары ( , ), называемой присоединенной парой с моментом, равным моменту силы относительно точки О.

Рис. 8
Приведение произвольной плоской системы сил к точке (основная теорема статики для произвольной плоской системы сил)
Рассмотрим на примере трех сил. Пусть к телу в точках А, В, С приложена плоская система сил { , , } (рис. 9). Выберем произвольную точку О, перенесем в нее силы , , .
Согласно лемме
Пуансо получим сходящуюся систему сил
{
,
,
![]() }
и систему пар (
,
}
и систему пар (
,
![]() ),
(
,
),
(
,
![]() ),
(
,
),
(
,
![]() )
с моментами М1, М2, М3, равными моментам
сил
,
,
относительно точки О.
)
с моментами М1, М2, М3, равными моментам
сил
,
,
относительно точки О.
Сложив , , по правилу многоугольника, получим:
![]() .
(7)
.
(7)
Вектор
![]() ,
равный геометрической сумме сил системы,
называется главным вектором данной
системы сил.
,
равный геометрической сумме сил системы,
называется главным вектором данной
системы сил.
Теперь сложим пары сил, в результате получим пару сил с моментом
![]() .
(8)
.
(8)
М0 – равен алгебраической сумме моментов сил и называется главным моментом системы сил относительно точки.

Рис. 9
Теорема Вариньона. Если система сил приводится к равнодействующей, то момент равнодействующей относительно любой точки равен сумме моментов всех сил системы относительно той же точки.
Доказательство:
Пусть система сил { , , } имеет равнодействующую
![]() (рис.
10),
(рис.
10),
приложенную в
некоторой точке О1 плоскости действия
сил. Перенесем вектор
![]() в
точку О, при этом согласно лемме Пуансо
необходимо добавить пару (
в
точку О, при этом согласно лемме Пуансо
необходимо добавить пару (![]() ,
,
![]() )
с моментом М0=М(
).
Но М0 – главный момент системы сил
относительно точки О, который равен
алгебраической сумме моментов всех сил
системы относительно этой точки:
)
с моментом М0=М(
).
Но М0 – главный момент системы сил
относительно точки О, который равен
алгебраической сумме моментов всех сил
системы относительно этой точки:
![]() .
Следовательно
.
Следовательно
![]() .
.
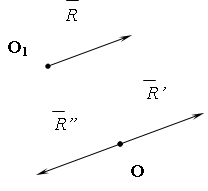
Рис. 10
Следствия из теоремы:
1. Главный вектор не изменится при изменении центра приведения.
2. Главный момент при перемене центра приведения изменится на величину момента силы , приложенной в точке О, относительно нового центра.
Условия равновесия
Свободное твердое тело под действием произвольной плоской системы сил находится в равновесии, если главный вектор и главный момент этой системы относительно любой точки равны нулю: =0, М0=0.
Разложим по осям получим:

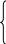 (9)
(9)
Условие равновесия для произвольной пространственной системы сил:

 (10)
(10)

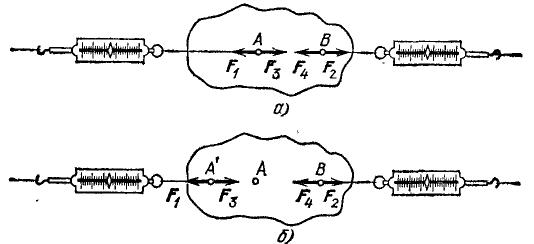 Рис.
97. а) В точках A и В на тело действуют
равные силы f1
и f2
противоположного направления. В
теле возникает деформация и появляются
упругие силы f3
и f4.
б) При перенесении силы f1
из точки А в точку А’ равновесие не
нарушается.
Рис.
97. а) В точках A и В на тело действуют
равные силы f1
и f2
противоположного направления. В
теле возникает деформация и появляются
упругие силы f3
и f4.
б) При перенесении силы f1
из точки А в точку А’ равновесие не
нарушается.