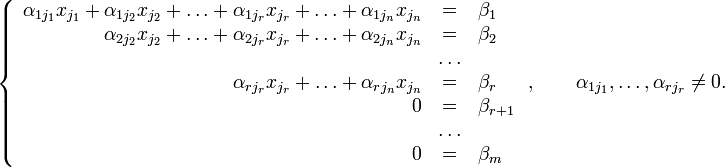Определение решения слау. Преобразование системы уравнений не меняющее множество решений системы.
Система
m линейных уравнений с n неизвестными
(или, линейная система) в линейной алгебре
— это система уравнений вида
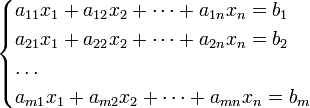
Решение
СЛАУ
Ме́тод
Га́усса — классический метод решения
системы линейных алгебраических
уравнений (СЛАУ). Это метод последовательного
исключения переменных, когда с помощью
элементарных преобразований система
уравнений приводится к равносильной
системе ступенчатого (или треугольного)
вида, из которого последовательно,
начиная с последних (по номеру) переменных,
находятся все остальные переменные.
П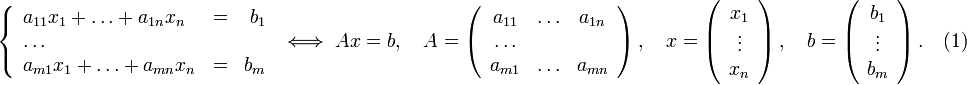 усть
исходная система выглядит следующим
образом
усть
исходная система выглядит следующим
образом
Матрица
A называется основной матрицей системы,
b — столбцом свободных членов.
Тогда
согласно свойству элементарных
преобразований над строками основную
матрицу этой системы можно привести к
ступенчатому виду(эти же преобразования
нужно применять к столбцу свободных
членов):
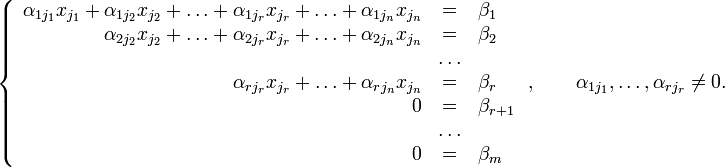
Далее
подставляем по очереди в исходное
выражения, получая элементы.
Метод
Крамера (правило Крамера) — способ
решения квадратных систем линейных
алгебраических уравнений с ненулевым
определителем основной матрицы (причём
для таких уравнений решение существует
и единственно). Назван по имени Габриэля
Крамера (1704–1752), придумавшего метод.
http://ru.wikipedia.org/wiki/%CC%E5%F2%EE%E4_%CA%F0%E0%EC%E5%F0%E0


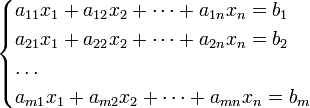
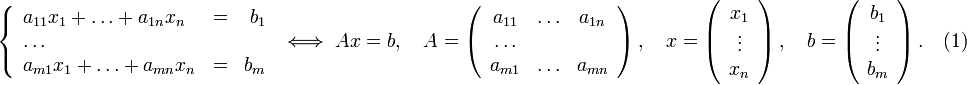 усть
исходная система выглядит следующим
образом
усть
исходная система выглядит следующим
образом