1

Матрица – совокупность строк и столбцов, на пересечении которых расположены её элементы. Количество строк и столбцов задают размеры матрицы.

Виды матриц:

Квадратная: Если её размеры n на n.

Диагональная: Если матрица квадратная и все элементы, кроме главной диагонали равны нулю.

Единичная: Диагональная, все элементы главной диагонали равны единице.

Нулевая: Если все элементы равны нулю.

Треугольная: если элементы выше или ниже главной диагонали равны нулю. Если выше, то нижнетреугольная, если ниже – то верхнетреугольная.

Операции над матрицами:

Транспонирование: 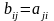, для всех i, j (или, проще говоря, строки становятся столбцами).

Сложение: Две матрицы одинакового размера можно складывать. В итоге получится новая матрица такого же размера, у которой С_ij = A_ij + B_ij.

Умножение на число: Матрицу можно умножить на число. Тогда С_ij = a * A_ij.

Умножение матрицы на матрицу: Произведение матрицы A размера m на n и матрицы B размером n на p называется матрица C размером m на p, у которой

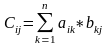
2

Перестановкой множества называют любой упорядоченный набор из n элементов этого множества, среди которых нет одинаковых(интернет).

Всевозможные расположения n различных элементов, отличных друг от друга только порядком, называют перестановками из n элементов(лекции).

Например, есть множество {1,2,3,4,5}. Перестановками являются: {1,2} {3,4,5} {5,1}. Не являются: {1,2,3,4,6} {1,2,3,1}. Начальной перестановкой является перестановка {1,2,3,4,5}

Теорема о количестве перестановок: Существует ровно n! перестановок множества из n элементов.

Доказательство: По методу индукции. Пусть есть множество {1}. Тогда возможное количество перестановок одно – {1}.

Пусть существует ровно (n-1)! перестановок множества из (n-1) элементов. Добавим этому множеству еще один элемент n. Он может стоять на любом месте в исходном множестве. Поставим его на первое место. Исходя из предположения, получим (n-1)! перестановок. Поставим на 2,3..n место, получим n! перестановок. Что и требовалось доказать.

Говорят, что пара чисел (i, j) образуют инверсию, если i > j, но i стоит левее j. Например, в перестановке {5,4,6,7} образуют инверсию {5,4}.

Перестановка называется четной, если количество её инверсий четно. А нечетной, если количество перестановок нечетно.

Подстановка – перестановка местами элементов множества, при этом должны получится все элементы исходного множества и все по одному разу. Если переставляются только два элемента, то такую подстановку называют транспозицией.

Примеры: 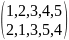– подстановка, 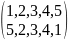– транспозиция.

3

Определитель квадратной матрицы А n-ого порядка называется алгебраическое сумма всевозможных произведений элементов, взятых по одному из каждого столбца и строки матрицы А. Для определения знака, с каким произведения входит в детерминант, надо в его индексах подставить подстановку 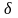из которой берутся элементы произведения со знаком плюс, если количество подстановок четное и минус, если количество нечетное(лекции).

Определитель 2-го порядка:

.

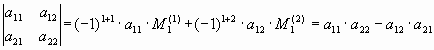Определитель 3-го порядка:

.

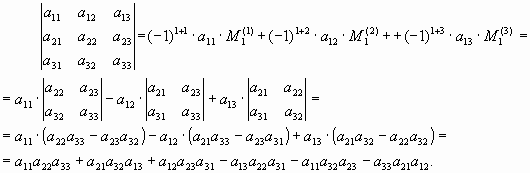4

Определитель транспонированной матрицы равен определителю исходной матрицы. Доказательство: каждый член исходного определителя будет в разных строках/столбцах после транспонирования.

5

Каждая перестановка строк в определителе меняет знак определителя.

Доказательство: если произведение является членом исходного детерминанта, то все его множители и в новом детерминанте окажутся в разных строках/столбцах.

6

Умножение строки на число, умножение строки определителя на число и её добавления к другой строке не изменяют значение определителя.

Доказательство: вытекает из следующих свойств: определитель с двумя пропорциональными строками равен нулю и

7