4. Кодирование дискретных источников

4.1. Равномерное кодирование для дискретных источников без памяти

Пусть ДИБП выдает символы из алфавита , , через каждые секунд. Согласно (2.7) и (2.10), энтропия источника на символ , где равенство верно, если все символы равновероятны. Изучим схему блокового кодирования источника равномерным кодом с основанием . Каждому символу источника взаимно однозначно соответствует последовательность из символов кода. Скорость кодирования (затраты на кодирование) источника , если - целая степень основания , иначе . Здесь - оператор взятия целой части числа. Так как , то .

Эффективность кодирования ДИБП равна . Равномерный код наиболее эффективен ( ), если , где , и символы источника равновероятны. Если , но символы источника равновероятны, то . Максимально возможная разность . Если , эффективность системы кодирования высока. Если относительно мало, эффективность кода можно увеличить. Перейдем от посимвольного кодирования к кодированию последовательностей символов источника с символами в каждой. Время кодирования каждой из них равно . Для кодирования надо выбрать разных кодовых слов. При длине кода есть возможных кодовых слов. Значит, , и минимальное целое значение . Теперь среднее число символов кода на символ источника , а эффективность кодирования . Эффективность кодирования (скорость кодирования) увеличилась (уменьшилась) по сравнению с посимвольным кодированием. Для достаточно большого можно обеспечить эффективность процедуры кодирования, как угодно близкую к . Бесшумные коды, описанные выше, не приводят к искажениям ввиду однозначности процедуры кодирования.

Скорость кодирования можно уменьшить, смягчая условия однозначности процесса кодирования. Выберем наиболее вероятных -символьных блоков из общего числа . Закодируем их однозначно. Остальные блоков представим одним оставшимся кодовым словом. Эта процедура кодирования вызывает ошибку декодирования, когда источник выдает такой маловероятный блок. Используя эту процедуру, Шеннон доказал следующую теорему кодирования источника .

Теорема кодирования источника I. Пусть - это ансамбль символов ДИБП с конечной энтропией . Блоки из символов источника кодируются в двоичные кодовые слова длиной . Для любого вероятность ошибки декодирования можно сделать как угодно малой, если

(4.1)

и достаточно велико. Наоборот, если

(4.2)

то сколь угодно близка к при достаточно большом .

Итак, среднее число битов на символ ДИБП для кодирования его выхода с произвольно малой вероятностью ошибки декодирования ограничено снизу энтропией источника , если .

4.2. Неравномерное кодирование для дискретных источников без памяти

Наша цель – создать систематическую процедуру построения эффективных кодов переменной длины, удовлетворяющую условиям:

1. возможность однозначного декодирования;

2. минимум среднего числа символов кода на один символ источника

, где - длина слова, кодирующего символ источника.

Символы кодовых слов посредством сигналов передаются по каналу связи. Такие сигналы можно интерпретировать как канальные.

В методе энтропийного кодирования источника значение минимизируется, когда более вероятным символам источника сопоставляются более короткие кодовые слова. Примером такого кодирования служит код Морзе (см. п. 1.2). Но у неравномерного кода на приемной стороне неизвестны границы кодовых слов. Поэтому процедура декодирования сообщения может быть неоднозначной. Например, если букве сопоставлено слово , букве - , а букве - , нельзя найти по принятой комбинации , передавались ли буква или пара букв и . Однозначное декодирование обеспечено лишь для префиксных кодов. В них ни одно кодовое слово не является началом другого. Необходимые и достаточные условия их существования определены следующей теоремой .

Теорема об условиях существования префиксного кода. Необходимым и достаточным условием существования - ичного префиксного кода с кодовыми словами длины служит выполнение неравенства Крафта:

(4.3)

Докажем достаточность. Пусть множество удовлетворяет (4.3). Перепишем (4.3): где - число последовательностей длины , и . Раскрыв сумму, получим: . Так как все , то отсюда последовательно найдем систему неравенств

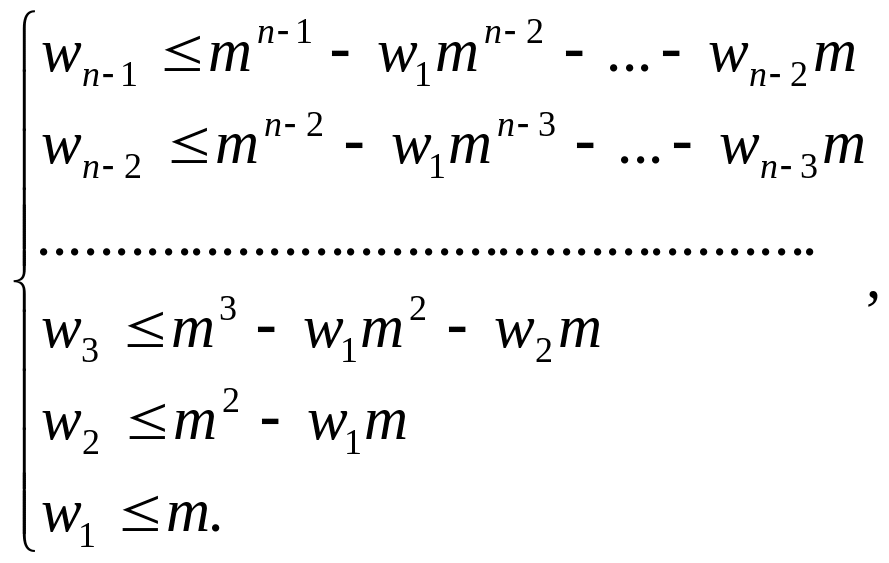
для построения кода с заданным набором кодовых длин. Выберем слов длиной , используя разные буквы из алфавита объема . Остается неиспользованных символов (свободных префиксов длины ). Можно построить слов длиной , добавляя к ним по символу из алфавита объемом . Из этих слов длины выберем произвольных слов. Остается свободных префиксов длины . Добавляя к ним разные символы из алфавита объема , получим слов длиной . Из них выберем произвольных слов и т.д. Продолжая, построим префиксный код, длины слов которого удовлетворяют (4.3). С учетом (4.3) докажем теорему префиксного кодирования источника (без шумов) .

Теорема кодирования источника II. Пусть - ансамбль символов источника без памяти с конечной энтропией и выходными символами , , с соответствующими вероятностями , , выбора этих символов. Есть возможность создать префиксный код с такой средней длиной , что

(4.4)

Для кодовых слов длины , , с учетом (2.7) выразим . Но ( ). Тогда 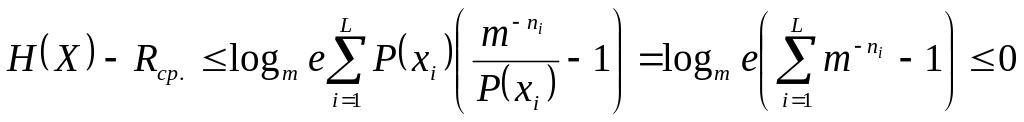, где последнее неравенство следует из (4.3). Итак, обоснована нижняя граница в (4.4). Предположим, что , , - целые числа, выбираемые из условия . Если неравенства просуммировать по , получим (4.3), для которого существует префиксный код. Логарифмируя неравенства , имеем: . Каждое из последних неравенств умножим на соответствующую вероятность . Суммируем их по ( ). Получим верхнюю границу, данную в (4.4).

Итак, префиксные коды переменной длины – это эффективные коды для любого ДИБП с символами, имеющими разные априорные вероятности. Неравномерное префиксное кодирование устраняет избыточность источника, вызванную неодинаковой вероятностью сообщений, и, тем самым, производит их сжатие. Опишем алгоритм построения таких кодов (алгоритм кодирования Хаффмена). Он требует знания априорных вероятностей символов , . Этот алгоритм посимвольного кодирования оптимален (среднее число кодовых символов в расчете на символ источника минимально). Получаемые кодовые слова удовлетворяют префиксному условию, что позволяет однозначно производить декодирование. Проиллюстрируем данный алгоритм кодирования на примере .

Пример 4.2.1. Возьмем ДИБП с символами , , имеющими заданные вероятности выбора. Надо построить двоичный код ( ).

Построим кодовое дерево (см. рис. 4.1). Символы источника расположим в порядке убывания их вероятностей. Пусть , , , , , и . Кодирование начнем с х наименее вероятных символов и . Их объединим (см. рис. 4.1). Верхнему ветвлению присвоим кодовый символ , а нижнему - . Сложим вероятности этих ветвей. Общему узлу присвоим суммарную вероятность . Теперь есть исходные символы: , и новый символ , полученный объединением и . На следующем этапе снова объединим наименее вероятных символа и с суммарной вероятностью из набора: . Переходу от символа присвоим кодовый символ , а переходу от символа - . Процедуру продолжим, пока не исчерпаем все возможные символы источника. Результат – кодовое дерево с ветвями, содержащими искомые кодовые слова.

Кодовые слова (см. табл. 4.1) получаются, если двигаться от самого правого узла дерева, переходя к самому левому узлу. Среднее число кодовых символов на символ источника бит/символ, а энтропия источника - бит/символ.

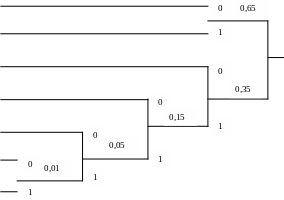0,35

0,30

0,20

0,10

0,04

0,005

0,005

Рис. 4.1. Построение кодового дерева

Таблица 4.1. Кодовые слова кода Хаффмена и их характеристики

Символ	Вероятность	Собственная информация	Код
	0,35	1,5146	00
	0,30	1,7370	01
	0,20	2,3219	10
	0,10	3,3219	110
	0,04	4,6439	1110
	0,005	7,6439	11110
	0,005	7,6439	11111

На предпоследнем шаге процедуры кодирования был равный по вероятности выбор между и . Здесь были соединены и . Вместо этого в альтернативном коде можно было бы соединить и , получив символ . На последнем шаге построения кодового дерева соединялись бы символы и . Для альтернативного кода среднее число битов на символ тоже равно , как и для кода на рис. 4.1. То есть, полученные коды одинаково эффективны. Назначение верхнему переходу и - нижнему (менее вероятному) переходу, выбрано произвольно. Поменяв местами и , получим еще два эффективных префиксных кода.

Более эффективна, чем посимвольное кодирование, процедура укрупнения алфавита, основанная на кодировании блоков из символов одновременно. Тогда границы в (4.4) уже другие: так как энтропия -символьного блока от ДИБП равна , и - среднее число битов в -символьном блоке. Разделив последнее неравенство на , получим

(4.5)

где - среднее число битов на исходный символ. Значение можно сделать как угодно близким к , выбирая достаточно большим. То есть, выход ДИБП можно закодировать неравномерным кодом со средним числом кодовых символов на символ алфавита источника, сколь угодно близким к энтропии источника .