Структурные средние (мода и медиана)

Мода (Мо) – это наиболее часто повторяющаяся величина признака (варианта), т.е. признак с наибольшей частотой. По сгруппированным данным мода определяется по формуле: ,

где Х0 – нижняя граница модального интервала (интервала с наибольшей частотой); i – величина модального интервала; fМо, fМо-1, fМо+1 – соответственно частоты модального, предмодального и послемодального интервалов.

Медиана (Me) – это величина, которая делит ранжированный ряда пополам. Для определения медианы сначала находят ее место в ряду по формуле , где n – число членов ряда ( ). Если число единиц чётное, то место медианы в ряду определяется как . По сгруппированным данным: , по несгруппированным: 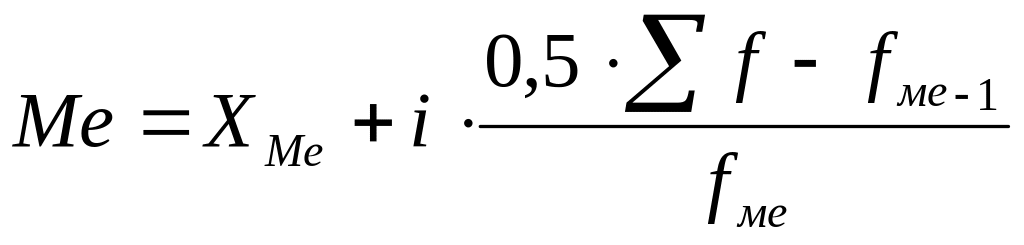, где ХМе – нижняя граница медианного интервала; i – величина интервала; – сумма всех частот; – сумма частот, предшествующего медианному интервалу; – частота медианного интервала.

Свойство медианы заключается в том, что сумма абсолютных отклонений значений признака от медианы меньше, чем от любой другой величины. Применение медианы позволяет получить более точные результаты, чем при использовании других форм средних. Мода и медиана широкого применяются при статистических методах контроля качества продукции, при оценке качества передачи информации, надежности работы средств труда.

11. Понятие вариации массовых явлений. Показатели вариации, их свойства, формулы расчета и экономический смысл.

Вариация признака – различие индивидуальных значений признака внутри изучаемой совокупности. Она возникает в результате того, что его индивидуальные значения складываются под совокупным влиянием разнообразных факторов (условий), которые по-разному сочетаются в каждом отдельном случае. Колебания отдельных значений характеризуют показатели вариации. Различают вариацию признака: случайную и систематическую. Систематическая вариация помогает оценить степень зависимости изменений в изучаемом признаке от определяющих ее факторов.

Для всех показателей вариации общим является следующие:

• если показатель вариации близко к 0 (т.е. индивидуальные значения признака мало отличаются друг от друга), то средняя арифметическая будет достаточно показательной (надежной) характеристикой данной совокупности;

• если же ряд распределения характеризуется значительным рассеиванием (величина показателя вариации сильно отличается от нуля, является большой), то средняя арифметическая будет ненадежной и ее практическое применение будет ограничено.

Анализ систем вариации позволяет оценить степень зависимости различий значений признака от влияющих на них факторов.

К абсолютным показателям относятся:

• размах вариации (R) – показатель, показывающий насколько велико различие между единицами совокупности, имеющими наибольшее и наименьшее значение признака: R = x_max - x_min;

• среднее линейное отклонение ( ) – это среднее арифм-кое из отклонений индивидуальных значений от средней: – для несгруппированных данных; – для сгруппированных;

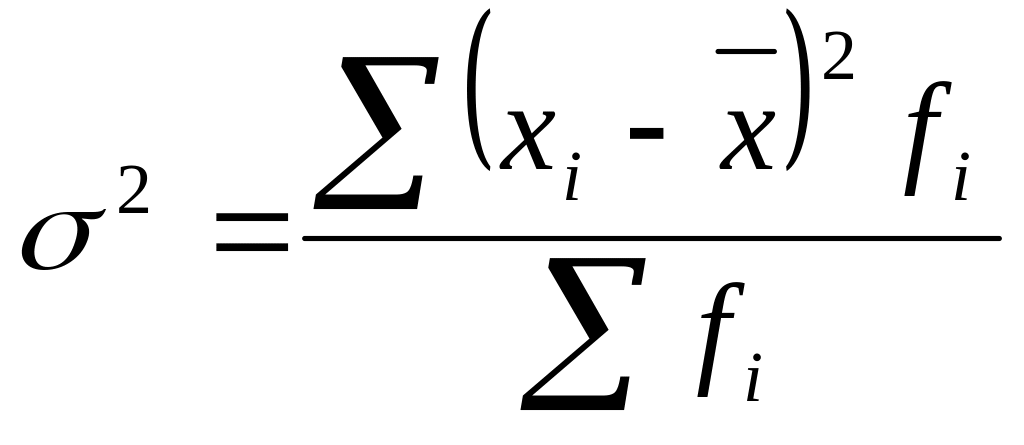• дисперсия – средний квадрат отклонений индивидуальных значений признака от их средней величины: – для несгруппированных данных; – для сгруппированных;

• среднее квадратическое отклонение – это корень квадратный из дисперсии : простое для несгруппированных данных , взвешенное для сгруппированных .

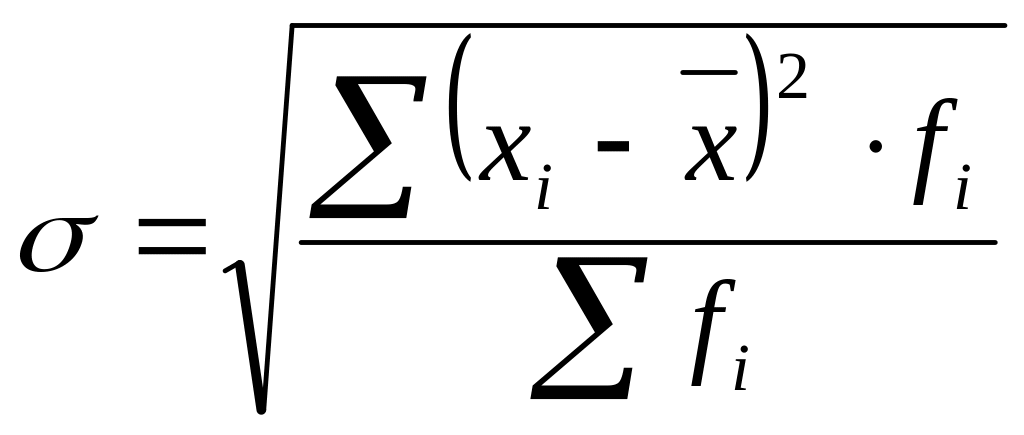К относительным показателям относятся:

• коэффициент осцилляции показывает относительную колеблемость крайних значений признака вокруг средней: ;

• относительное линейное отклонение характеризует долю усредненного значения абсолютных отклонений от средней величины: ;

• коэффициент вариации – показатель колеблемости для оценки типичности средней величины, если < 40%, то совокупность однородная, колеблемость признаков умеренная: .

Дисперсия, ее свойства и методы расчета. Дисперсия – средний квадрат отклонений, определяемый как средняя из отклонений, возведенных в квадрат.

_{Для несгруппированных данных : , для сгруппированных:}

Дисперсия обладает рядом свойств, которые позволяют упростить ее расчеты.

1. Если из всех значений вариант отнять какое-то постоянное число А, то средний квадрат отклонений от этого не изменится:

2. Если все значения вариант разделить на какое-то постоянное число А, то средний квадрат отклонений уменьшится от этого в А² раз, а среднее квадратическое отклонение – в А раз:

3. Дисперсия, рассчитанная от постоянной величины, больше дисперсии, рассчитанной от средней, на квадрат разности между средней величиной и постоянной, т.е. на : или

4. Дисперсия от средней имеет свойство минимальности, т.е. она всегда меньше дисперсий, исчисленных от любых других величин. В этом случае, когда А = 0 формула принимает вид: 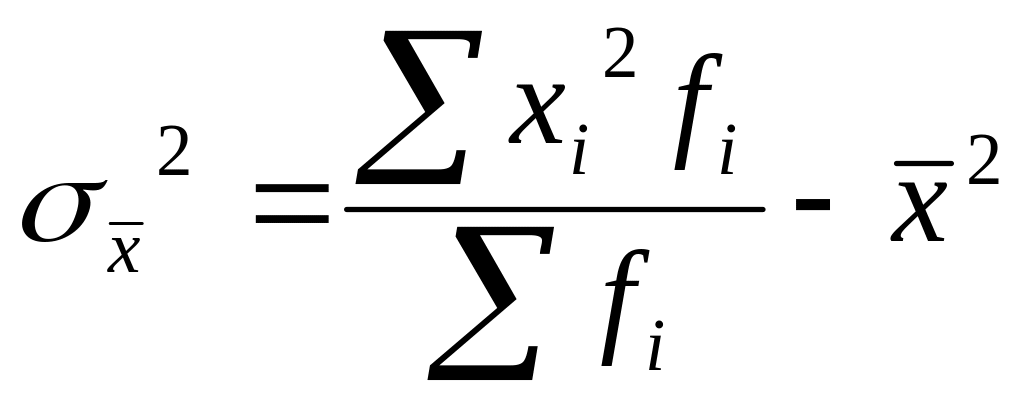или = ² – , где ² =

Дисперсия альтернативного признака Альтернативным называется признак, который может принимать только 2 значения: наступление или ненаступление события. Условно считается, что альтернативный признак равен 1, если событие наступило и равен 0, если событие не наступило. Доля единиц совокупности, обладающих изучаемым признаком – p , а не обладающих им q, .

Среднее значение альтернативного признака равно:

Дисперсия альтернативного признака определяется следующим образом:

Т.о. дисперсия альтернативного признака равна произведению доли единиц, обладающих признаком, и доли единиц, не обладающих им. Если значения p и q неизвестны, то для дисперсии берется самая большая их величина: p = q = 0,5.

Дисперсия альтернативного признака используется в выборочном наблюдении.