6 Нули функции. Изолированные особые точки

6.1 Нули аналитической функции

Определение. Точка называется нулем аналитической функции порядка (или кратности) , если . В случае точка называется простым нулем.

Теорема. Для того, чтобы точка была нулем -гo порядка функции , аналитической в точке , необходимо и достаточно, чтобы в некоторой окрестности этой точки имело место равенство , где аналитична в точке и .

Пример 1. Найти нули функции и определить их порядки.

Из уравнения находим точки , – нули данной функции. Имеем: , , т.е. точки – нули второго порядка данной функции.

Пример 2. Найти нули функции и определить их порядки.

Полагая , получаем, что или . Решая эти уравнения, находим нули функции . Пусть ; тогда можно представить в виде , где функция является аналитической в точке , причем . Это означает, что точка есть нуль третьего порядка. Аналогично доказывается, что и точка является нулем третьего порядка. Исследуем нули . Производная в точках отлична от нуля. Следовательно, – простые нули функции .

6.2 Изолированные особые точки

Определение 1. Точка называется особой точкой аналитической функции , если в этой точке аналитичность функции нарушается.

Определение 2. Точка называется изолированной особой точкой функции , если существует окрестность этой точки с исключенной точкой , в которой аналитична, кроме самой точки .

Существует три типа изолированных особых точек. Приведем их определения.

Определение 3. Точка называется устранимой особой точкой функции , если разложение этой функции в ряд Лорана в окрестности точки не содержит главной части.

Определение 4. Точка называется полюсом кратности функции , если в разложении функции в ряд Лорана в окрестности точки главная часть разложения содержит конечное число членов, причем младшим отличным от нуля коэффициентом является .

Определение 5. Точка называется существенно особой точкой функции , если главная часть разложения функции в ряд Лорана в окрестности точки содержит бесконечное число членов.

Приведем критерии типа изолированных особых точек.

1) для того чтобы точка была устранимой особой точкой функции , необходимо и достаточно, чтобы существовал ;

2) для того чтобы точка была полюсом кратности функции , необходимо и достаточно, чтобы , .

3) для того чтобы точка была существенно особой точкой функции , необходимо и достаточно, чтобы не существовал.

Полезна следующая теорема.

Теорема (связь между нулями и полюсами). Для того чтобы точка была полюсом порядка функции , нужно, чтобы она была нулем -го порядка функции .

Пример 1. Для функции особой точкой является .

;

значит есть устранимая особая точка.

Пример 2. Для функции , является особой точкой. Так как , – это полюс. Рассмотрим функцию , так как , ; , ; , ; , ; , , значит – нуль пятого порядка функции и по теореме о связи между нулями и полюсами, точка является полюсом пятого порядка для функции .

Пример 3. Для функции является особой точкой. Разложение в ряд Лорана: в главной части содержит бесконечное число членов; это существенно особая точка.

Пример 4. Найти все особые точки функции 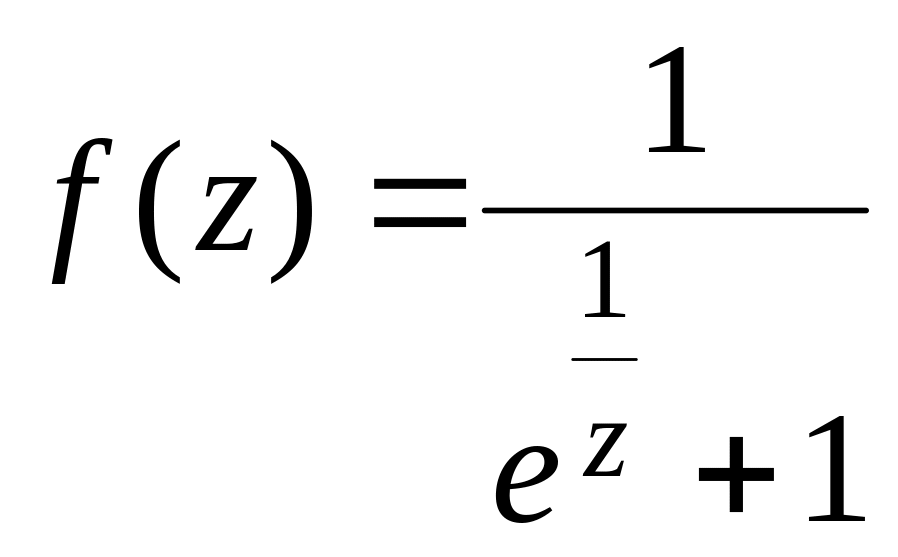и определить их тип.

Особыми точками являются точка и точки, в которых знаменатель обращается в нуль. Имеем , откуда , причем эти точки являются нулями первого порядка. Следовательно, в точках , функция имеет простые полюса. Точка не является изолированной особой точкой, так как она является пределом полюсов: , это означает, что любая окрестность точки содержит бесконечное число особых точек .

9