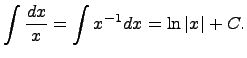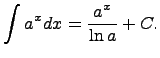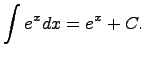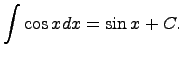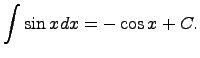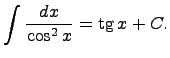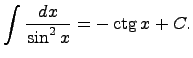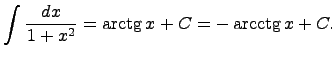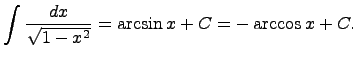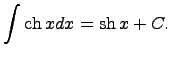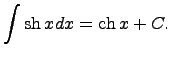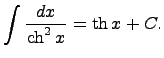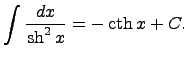1)Предел последовательности, определение
Определение.
Число а называется пределом
последовательности
 ,
если для любого
,
если для любого
 существует номер N
такой, что при всех n>N
выполняется неравенство
существует номер N
такой, что при всех n>N
выполняется неравенство

числовая последовательность – это функция натурального аргумента: xn = f(n)
Пример 1. Доказать,
что
 (указать
(указать
 ).
).
Решение. Неравенство
из определения предела последовательности,
которое мы должны решить относительно
n, принимает вид
 Пусть
Пусть
 .
Тогда
.
Тогда ,
откуда
,
откуда
 ,
следовательно, в качестве N
можно взять
,
следовательно, в качестве N
можно взять
 .
Здесь
.
Здесь
 -
целая часть числа
-
целая часть числа
 ,
то есть наибольшее целое число, не
превосходящее
.
Если, например,
,
то есть наибольшее целое число, не
превосходящее
.
Если, например,
 ,
то условиям задачи отвечают натуральные
числа
,
то условиям задачи отвечают натуральные
числа
 ,
то есть
,
то есть
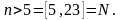
2)Бесконечно малые и их свойства
Функция y=f(x) называется бесконечно
малой при x→a или
при x→∞,
если ![]() или
или ![]() ,
т.е. бесконечно малая функция – это
функция, предел которой в данной точке
равен нулю.
,
т.е. бесконечно малая функция – это
функция, предел которой в данной точке
равен нулю.
Если функция y=f(x) представима при x→aв виде суммы постоянного числа b и бесконечно малой величины α(x): f (x)=b+ α(x) то
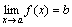 .
.Алгебраическая сумма двух, трех и вообще любого конечного числа бесконечно малых есть функция бесконечно малая.
Произведение бесконечно малой функции a(x) на ограниченную функцию f(x) при x→a (или при x→∞) есть бесконечно малая функция.
Отношение бесконечно малой функции α(x) на функцию f(x), предел которой отличен от нуля, есть бесконечно малая функция.
3)Теоремы о пределах.
Теорема. 1. Предел суммы есть сумма пределов.
Теорема. 2. Предел произведения есть произведение пределов.
Теорема. 3. Предел частного есть частное пределов (если знаменатель не обращается в 0).
Теорема. 4. Если u(x) z(x) v(x), и limx a u(x)=limx a v(x)=b, то limx a z(x)=b. ("Теорема о двух милиционерах").
Теорема
![]()
Следствие. ![]()
Теорема
 при
при ![]()
4)Предел функции
Пусть функция f (x) определена на некотором открытом интервале [b,c], содержащим точку x = a. (При этом не требуется, чтобы значение f (a) было обязательно определено.)
Число A называется пределом
функции f
(x) при ![]() ,
если для любого
,
если для любого ![]() существует
такое
существует
такое ![]() ,
что выполняется
,
что выполняется
![]()
при условии
![]()
Данное определение
предела известно
как ![]() -
определение или определение
Коши.
-
определение или определение
Коши.
Существует
также определение предела
функции по Гейне,
согласно которому функция f
(x)имеет
предел A в точке x
= a,
если для каждой последовательности ![]() ,
сходящейся к точке a,
последовательность
,
сходящейся к точке a,
последовательность ![]() сходится
к A.
сходится
к A.
5)Число е ,замечательный предел
Числом e называется предел
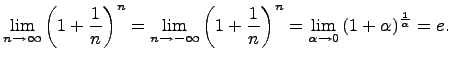
Это число иррациональное и приближенно равно е = 2.718281828.... Логарифмы с основанием е называются натуральными и обозначаются
![]()
Данный предел называют вторым замечательным пределом.
Многие примеры сводятся с помощью простых хамен ко второму замечательному пределу.
Рассмотрим несколько примеров решения на второй замечательный предел.
Пример 1 - найти предел используя второй замечательный предел
Найти предел:
![]()
Решение.
Преобразуем предел:

Используя свойства
пределов ,
а конкретно, что если функция ![]() непрерывна
в точке a,
то
непрерывна
в точке a,
то![]() ,
получим:
,
получим:
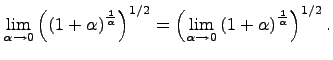
Замечаем, что можно применить второй замечательный предел и получаем ответ.
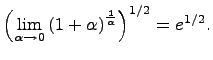
Исходный
предел равен: ![]() .
.
6)
![]() .
.
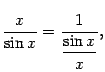
при
этом предел знаменателя ![]() --
это первый замечательный предел, равный
1 (и, следовательно, не равный 0). Числитель
правой части, равный 1, имеет предел 1.
Значит, по теореме о пределе отношения,
--
это первый замечательный предел, равный
1 (и, следовательно, не равный 0). Числитель
правой части, равный 1, имеет предел 1.
Значит, по теореме о пределе отношения,
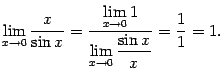
8)Непрерывность функции, разрывы
Пусть функция f(x) определена на некотором множестве Е и х0 – предельная точка множества Е.
Функция f(x) называется непрерывной в точке х0, если
1. Она определена в точке х0
2. Существует конечный предел
![]()
3. Этот предел равен значению функции в точке х0.
Иначе говоря, функция у=f(x) называется непрерывной в точке, если бесконечно малому приращению аргумента в этой точке соответствует бесконечно малое приращение функции, то есть

Разрывность функции
Итак, если хотя бы одно из трех условий непрерывности не выполняется, функция называется разрывной в точке х0, а сама точка x0-точкой разрыва. Если в точке x0 оба односторонних предела существуют и конечны, то разрыв называется разрывом первого рода. Пусть х0-точка разрыва первого рода, т.е.
Возможны два случая
1. f(x0+0)=f(x0-0)=L, но либо функция f(x) не определена в точке х0, либо f(x0) # L (то есть не выполнено либо первое либо третье условие непрерывности). В этом случае разрыв называется устранимым, так как если доопределить функцию в точке х0 или переопределить ее, положив f(x0)=L, функция f(x) станет непрерывной в точке х0.
![]() оба
односторонних предела существуют,
конечны и равны.
оба
односторонних предела существуют,
конечны и равны.
2. f(x0- 0) f(x0+0) B этом случае разрыв называется неустранимым.
Если же хотя бы один из односторонних пределов f(x0+0) или f(x0-0) не существует или бесконечен, то разрыв называется разрывом второго рода. Разрыв второго рода всегда неустранимый.
Если в точке х0 функции f(x) и g(x) непрерывны, то в этой же точке непрерывными являются и функции
![]()
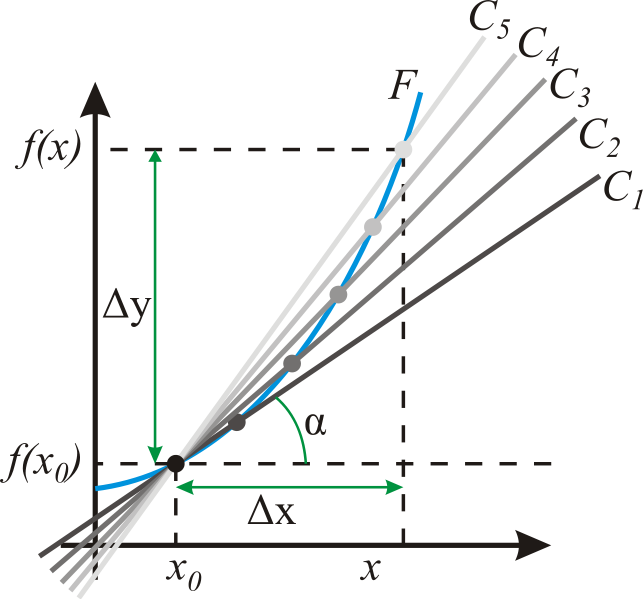
9)Производная ,геом смысл
Произво́дная (функции в точке) — основное понятие дифференциального исчисления, характеризующее скорость изменения функции (в данной точке). Определяется как предел отношения приращения функции к приращению ее аргумента при стремлении приращения аргумента к нулю, если такой предел существует. Функцию, имеющую конечную производную (в некоторой точке), называют дифференцируемой (в данной точке). Процесс вычисления производной называется дифференци́рованием. Обратный процесс — интегрирование.
Если
функция ![]() имеет
конечную производную в точке x0, то
в окрестности U(x0) её
можно приблизить линейной
функцией
имеет
конечную производную в точке x0, то
в окрестности U(x0) её
можно приблизить линейной
функцией
![]()
Функция fl называется
касательной к f в
точке x0. Число ![]() является
угловым коэффициентом
или тангенсом угла наклонакасательной
прямой.
является
угловым коэффициентом
или тангенсом угла наклонакасательной
прямой.
10)Дифференциал
Дифференциал+ (от лат. differentia — разность, различие) — линейная часть приращения функции.
Обычно дифференциал функции f обозначается df.
Для функций
Дифференциал функции ![]() в
точке
в
точке ![]() может
быть определён как линейная функция
может
быть определён как линейная функция
![]()
где f'(x0) обозначает производную f в точке x0.
Таким образом df есть
функция двух аргументов ![]() .
.
Дифференциал может быть определён
напрямую, т.е., без привлечения определения
производной как функция ![]() линейно
зависящая от h и для
которой верно следующее соотношение
линейно
зависящая от h и для
которой верно следующее соотношение
![]()
11)Таблица производных
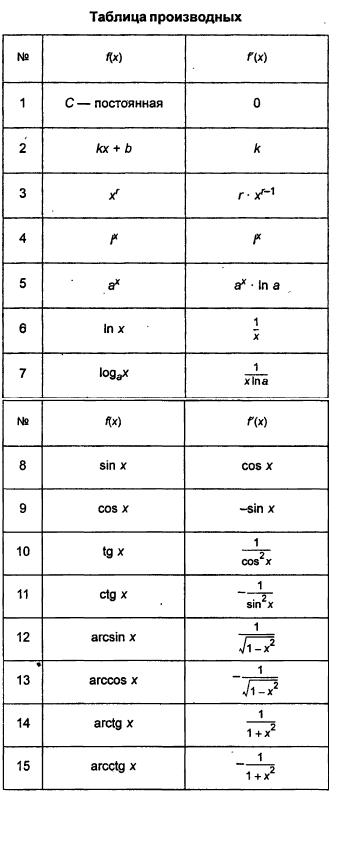
Доказательство
y = xn. Если n – целое положительное число, то, используя формулу бинома Ньютона:
(a + b)n = an+n·an-1·b + 1/2∙n(n – 1)an-2∙b2+ 1/(2∙3)∙n(n – 1)(n – 2)an-3b3+…+ bn,
можно доказать, что
![]()
Итак, если x получает приращение Δx, то f(x+Δx) = (x + Δx)n, и, следовательно,
Δy=(x+Δx)n – xn =n·xn-1·Δx + 1/2·n·(n–1)·xn-2·Δx2 +…+Δxn.
Заметим, что в каждом из пропущенных слагаемых есть множитель Δx в степени выше 3.
Найдем предел
![]()
Производная сложной и обратной функции
Производная сложной функции |
|
"Двухслойная" сложная функция записывается в виде
где u
= g(x) -
внутренняя функция, являющаяся, в
свою очередь, аргументом для внешней
функции f.
Если f и g -
дифференцируемые функции, то сложная
функция
Данная формула показывает, что производная сложной функции равна произведению производной внешней функции на производную от внутренней функции. Важно, однако, что производная внутренней функции вычисляется в точке x, а производная внешней функции - в точке u = g(x)! |
|
Пример 1 |
||||||||||
|
|
||||||||||
Найти
производную функции Решение. Поскольку
Обратная Рассмотрим функцию y = f(x), для которой существует обратная функция x = g(y). Теорема
5. Если
обратная функция x
= g(y) дифференцируема
и g'(y) ≠ 0,
то функцияy=f(x) дифференцируема,
и Доказательство Если аргумент x получит приращение Δx, то функция f получит приращение Δy = f(x + Δx) − f(x). С другой стороны, для обратной функции g приращения Δx, Δy связаны следующим образом: Δx=g(y + Δy) − g(y). Тогда получаем
13)Теоремы Теорема 1. Теорема Ро́лля утверждает, что если функция, имеющая производную на интервале, принимает в его концах равные значения, то её производная обращается в нуль в некоторой точке внутри интервала. (Теорема Ролля) Пусть функция f(x)
Тогда существует точка c (a, b) такая, что f'(c) = 0. Теорема 2. (Теорема Лагранжа) Пусть функция f(x)
Тогда существует точка с (a, b) такая, что
Формула (1) называется формулой Лагранжа, или формулой конечных приращений
Теорема 3. (Теорема Коши) Пусть функции f(x) и g(x)
Тогда существует точка c (a, b) такая, что
Формула (3) называется формулой Коши. 14)правило Лопиталя
Пусть
при x
Эта
теорема называется правилом
Лопиталя.
Она позволяет вычислять пределы
отношения функций, когда и числитель,
и знаменатель cтремятсялибо к нулю,
либо к бесконечности. Правило Лопиталя,
как говорят математики, позволяет
избавляться от неопределённостей
типа: 0 / 0 и 15)Возрастание и убывание функции Функция f(x) называется возрастающей в интервале (a,b), если при возрастании аргумента x в этом интервале соответствующие значения функции f(x) также возрастают, т.е. если
f(x2) > f(x1) при x2 > x1.
Функция f (x) называется убывающей в интервале ( a, b ) если при возрастании аргумента x в этом интервале соответствующие значения функции f (x) убывают, т.е. если f(x2) < f(x1) при x2 > x1. Из этого определения следует, что у убывающей в интервале ( a, b ) функции f (x) в любой точке этого интервала приращения x и y имеют разные знаки. 16)экстремумы функций Слово «экстремум» значит крайний. Точкой экстремума называется такая точка, в которой функция принимает крайние значения: наибольшее или наименьшее. Критической точкой функции называется такая точка ее области определения, в которой производная функции обращается в нуль или не существует. Критические точки функции, в которых она меняет возрастание на убывание или убывание на возрастание, называются точками экстремума. Если в точке экстремума функция меняет убывание на возрастание, то в этой точке достигается наименьшее значение хотя бы на небольшом участке ее области определения. Говорят, что такая точка является точкой локального минимума. Если в точке экстремума функция меняет возрастание на убывание, то в этой точке достигается наибольшее значение хотя бы на небольшом участке ее области определения. Говорят, что такая точка является точкой локального максимума.
17) Асимптота Определение (основное). Прямая называется асимптотой к кривой, если точка этой кривой неограниченно приближается к асимптоте при удалении точки по кривой в бесконечность. Определение. Если для функции выполняется, что
тогда прямая
называется вертикальной асимптотой к функции . Определение. Если существуют конечные пределы:
то прямая
называется горизонтальной асимптотой к функции . Определение. Если существуют конечные пределы:
и
тогда у функции существует наклонная асимптота
18)первообразные и неопределенные интегралы
Неопределенным
интегралом Задача нахождения неопределенного интеграла заключается в нахождении такой функции,производная которой равняется подынтегральному выражению. Данная функция определяется с точностью до постоянной, т.к. производная от постоянной равняется нулю. Например,
известно, что
Пусть
функция
то функция называется первообразной для функции . интегрирования – операции, обратной дифференцированию. 19)таблица интегралов
Здесь C - произвольная постоянная, т.к. производная от постоянной есть нуль, следовательно, неопределённый определяется с точностью до постоянной.
|
|||||||||||






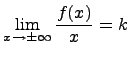
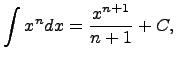 где
где