Понятие геометрического вектора.Основные определения, связанные с этим понятием (длина вект.,равенство вект.,нуль-вектор, коллиниарный и компланарный вект.,орт вектора.
Геометрический вектор-направленный отрезок, который можно перемещать параллельно ему самому. Направленный отрезок с началом в точке A и концом в точке B обозначается AB. Векторы обозначаются строчными латинскими буквами со стрелками: ↗а,↗в….
Таким образом, два направленных отрезка ∕AB и ∕CD, имеющие одинаковые длины и направления, изображают один и тот же вектор ↗а, и именно в этом случае будет равенство между векторами и направленными отрезками, например:↗а=∕АВ=∕СD
Длиной (или модулем)вектора ∕AB называется расстояние между точками A и B. Будем считать, что единица измерения длин выбрана и, говоря о длинах отрезков, не будем указывать, какой единицей они измеряются. Модуль вектора∕ AB обозначается символом |∕AB|. Вектор нулевой длины называется нулевым и обозначается символом ↗0. Векторы, лежащие на параллельных или совпадающих прямых, называются коллинеарными.Векторы,лежащие в праллельных или совпадающих плоскостях,называются компланарными.
Если угол между векторами равен π/2, то векторы называются ортогональными.
Линейные операции с геометрическими векторами. Законы, которые удовлетворяют эти операции. Разность векторов. Коллиниарные векторы.
Векторы, лежащие на параллельных или совпадающих прямых, называются коллинеарными.
Под линей.операц.над вект.понимают операции сложения,вычетания вект.и умнож.вект.на число.
1
)пусть
А и В произведение вект. А
/
ОА=/а
/а
/в
/а /в
О /а + /в Р
Правило треугольника: /ОВ=/а+/в
Сумму 2х вект.можно найти по правилу пар-ма. В этом случае /а и /в откладывают от 1 (.) : /ОС=/а+/в
/а
А
О
С
/а+/в
/в В
2) разность /а и /в:
/с=/а-/в /в+/с=/а /в+/с=/а
А
/а
О
/в В
Заметим,что в пар-ме,построенном на /а и /в, одна диагональ сумма /а и /в, а др.разностью /а и /в.: /а-/в=/а+/в
/а
/а+/в
/в
3)произведение /а на число λ-/λа такой, что длина |/ λ а|=|/ λ |*|/а| и направление / λ совпадает с направлением /а, если λ>0 и направление /λ противополож./а, если λ<0.
Из определения произведения вект.на число следует св-ва этого произвед.
1)/в=/ λа, то /а||/в
2)/а=|/а|*/а◦(орта)
Каждый вектор= произвед.его модуля на орту. св-ва л.о.над вект.:
1)переместит: /а+/в=/в+/а
2)сочитательн. /а+(/в+/с)=(/а+/в)+/с
Λ1/а(λ2/а)=(λ1*λ2)/а
3)распределительн. (/а+/в)λ=λ/а+λ/в
(λ1+λ2)/а=λ1/а+λ2/а
Эти св-ва позволяют проводить преобразования в л.о. над вект.,также,как в обычной алгебре,т.е.менять местами слагаемые,вводить скобки,группировать,выносить за скобки.
ДЕЛЕНИЕ ОТРЕЗКА В ЗАДАННОМ ОТНОШЕНИИ
допустим,дано:
М(х;у)
А(х1;у1) В(х2;у2)
Будем говорить М делит АВ в отношении λ,где λ>0 |АМ|/|МВ|=λ
Заметим,что в данном определении важен порядок в котор.указаны концы отрезка АВ. (.)А нач.отр.,В конец. Задача состоит в том,чтобы определить корд.(.)М, делящая отрезок в отнош.λ,если известны корд.(.) А и В.
Х=(х1+λх2)/(1+λ) (плоскость,пространство)
ПОНЯТИЕ РАДИУС ВЕКТОРА.РАЗЛОЖЕНИЕ ПРОИЗВОЛЬНОГО ВЕКТОРА ПО ОРТАМ КООРДИНАТНЫХ ОСЕЙ НА ПЛ. И В ПРОСТР.
Радиус-вектор точки - это называется вектор, начало которого совпадает с началом системы координат, а конец - с данной точкой.
Рассмотрим в прост.прямоуг.СК Оxyz. Выделим на корд.осях Ох,Оу,Оz единичные векторы(орты),обозначаемые /I,/j,/k.
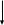
z
M
3
ϒ
/а
М
/k М2
О
ᵝ
у
/i ԃ /j
х М1 N
Выберем произвольный /а прост.и совместим его начало с нач.координат:/а=/ОМ.
Найдем проекции /а на корд.оси. проведем через конец вектора/ОМ плоскости,параллельные корд. Плоскостям. Точки пересечения этих плоскостей с осями обозначим соответственно через М1,М2,М3. Получим прямоугольный параллелепипед,одной из диагоналей которого является вектор/ОМ. Тогда прХ/а=|/ОМ1|,прУ/а=|/ОМ2|,прZ/а=|/ОМ3|.по определению суммы нечкольких векторов находим /а=/ОМ1+/M1N+/NМ.а т.к./M1N=/OM2,/NM=/OM3,то /а=/ОМ1+/ОМ2+/ОМ3.но /ОЬ1=|/ОМ1|*/i, /ОМ2=|/ОМ2|*/i, /ОМ3=|/ОМ3|*/к. обозначим проекции вектора /а=/ОМ на оси Ох,Оу,Оz соответственно через ах,ау,аz,т.е. |/ОМ1|=ах, |/ОМ2|=ау,|/ОМ3|=аz. Тогда из равенства=> /а=ах*/i+ay*/j+az*/k. Эта формула явл.основ. в векторном исчислении и назыв.разложением вект.по ортам корд осей. ах,ау,аz-коорд.вект.