Правило Лопиталя.

Найти если .

Найти .

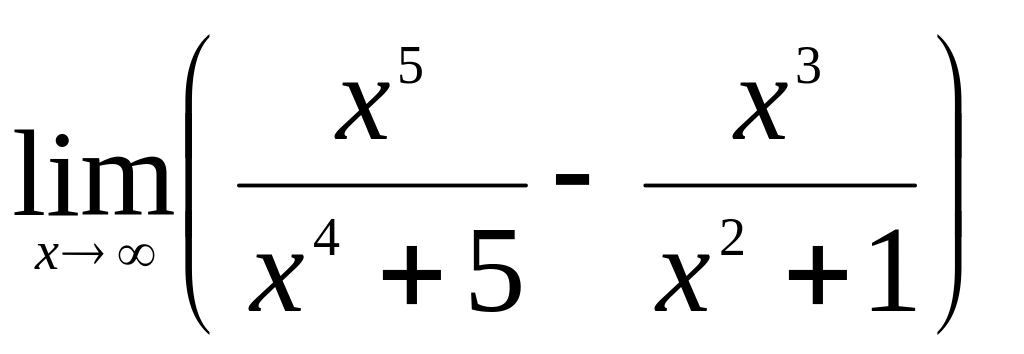Найти интервалы выпуклости и точки перегиба графика функции .

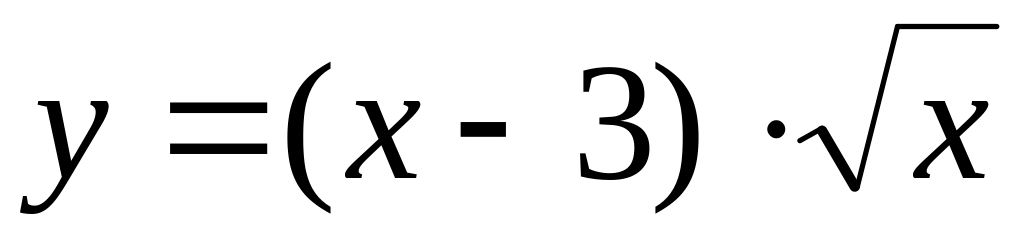Теорема Лагранжа о конечном приращении, следствия.

Найти если .

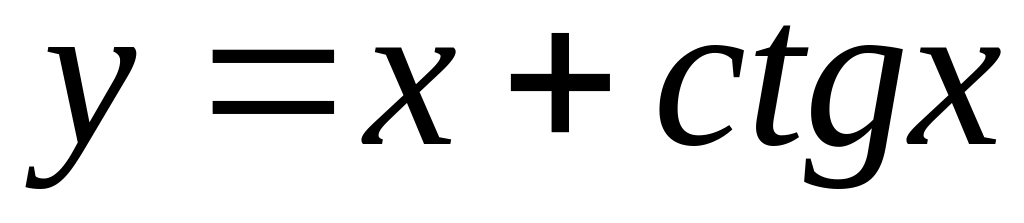Найти .

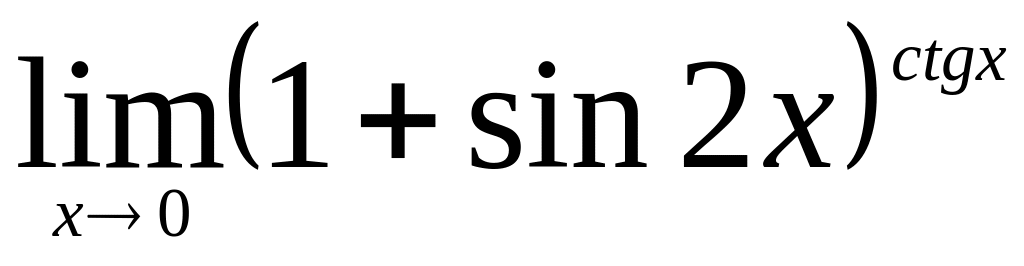Исследовать функцию на экстремум и найти промежутки монотонности .

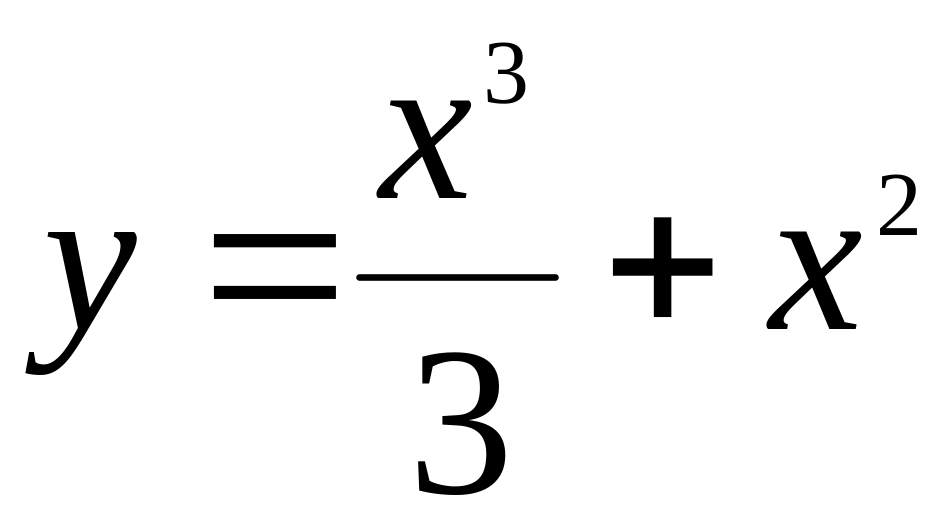Теорема Ролля, ее геометрический смысл.

Найти если .

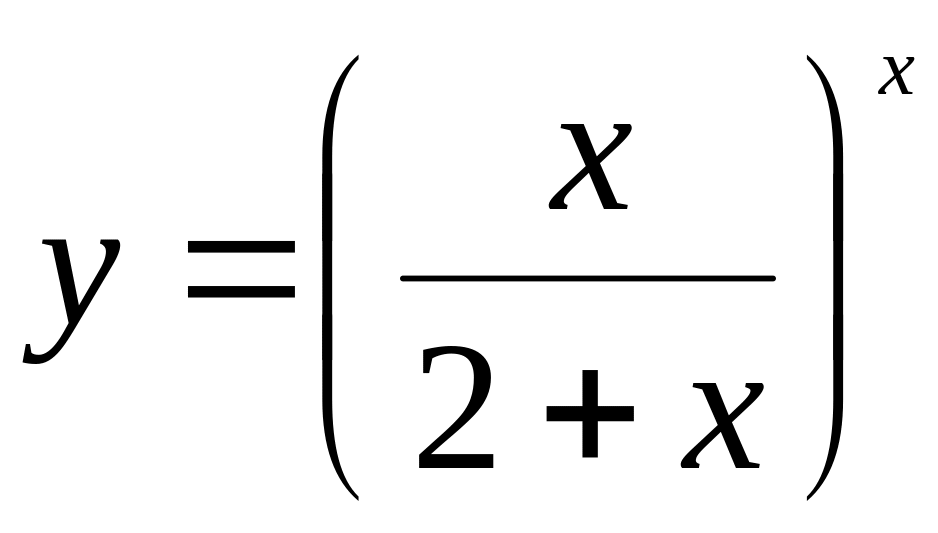Найти .

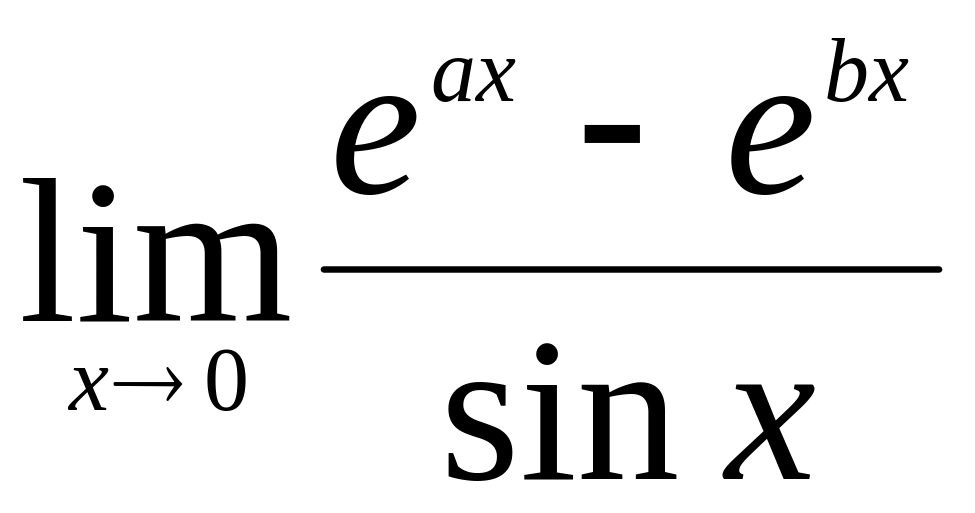Найти асимптоты графика функции .

Монотонные функции (определения), необходимый признак возрастания (убывания) функции.

Найти если .

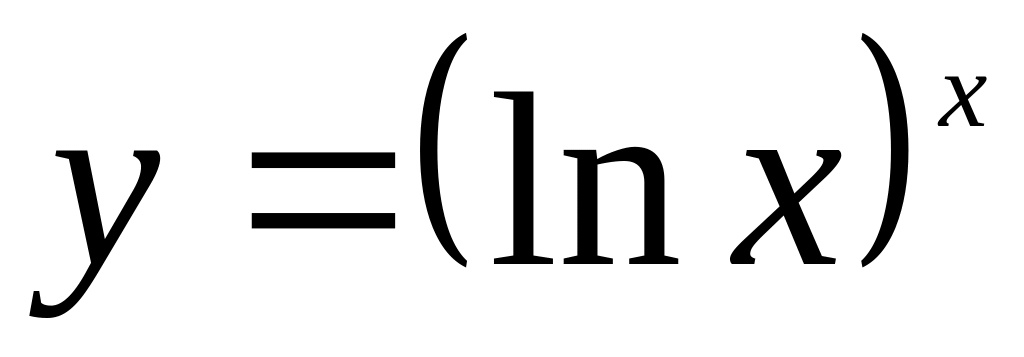Найти .

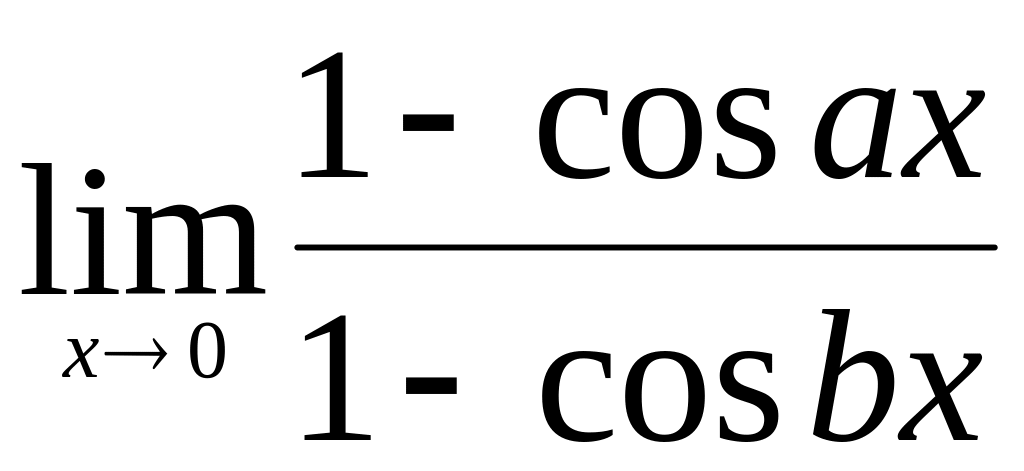Найти интервалы выпуклости и точки перегиба графика функции .

Монотонные функции (определения), достаточный признак возрастания (убывания) функции.

Найт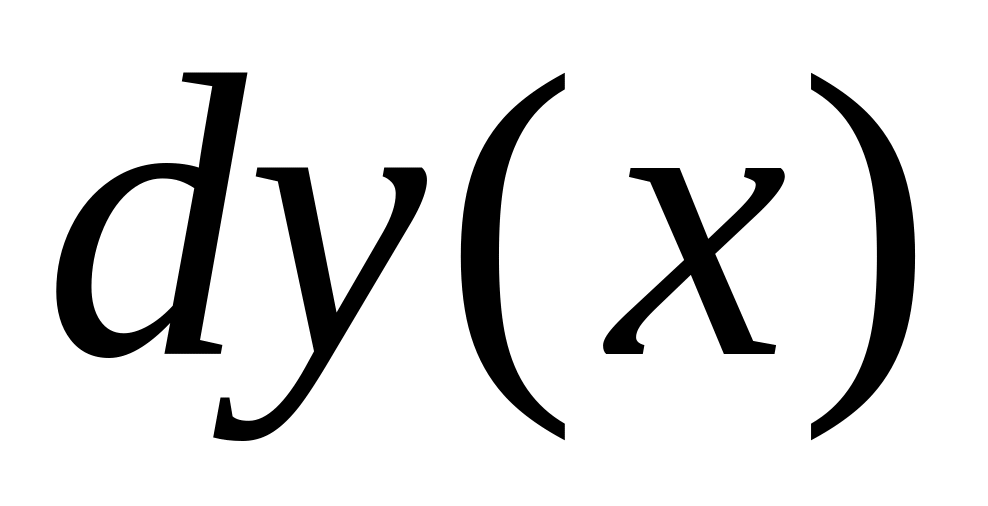и , если .

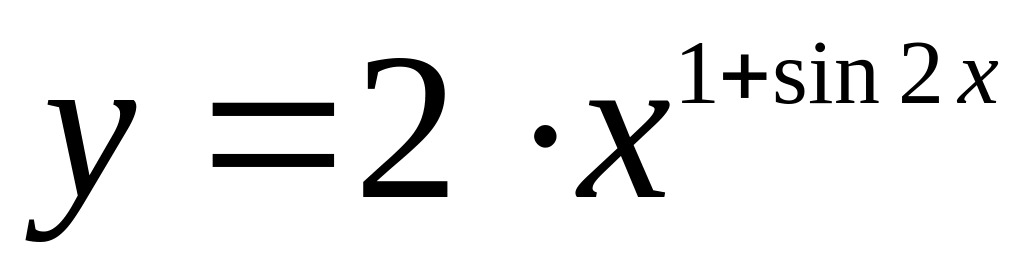Найти .

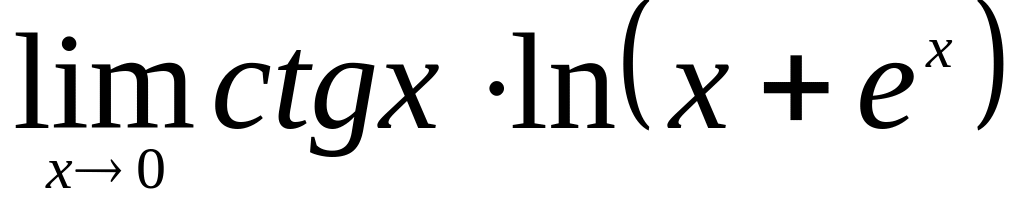Найти интервалы монотонности и экстремум функции .

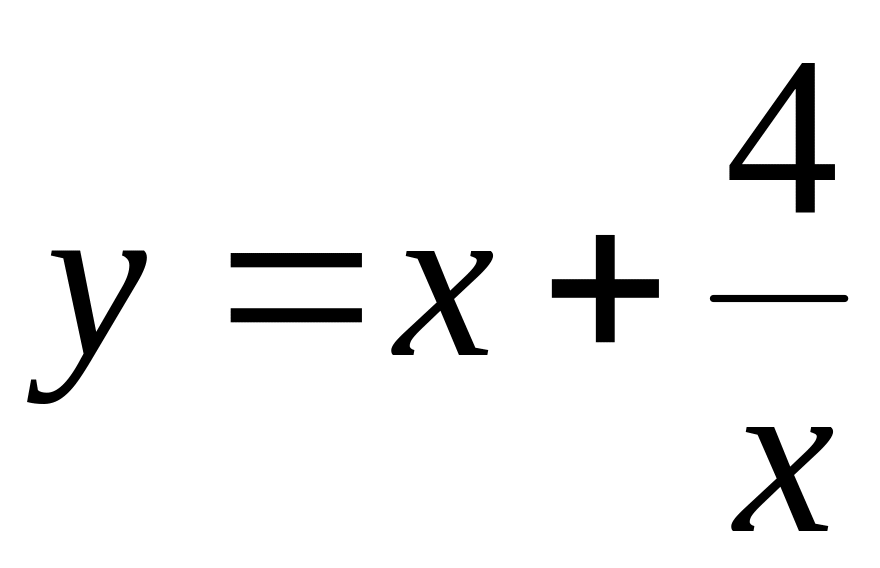Локальный экстремум функции (определения), необходимый признак существования локального экстремума функции.

Найт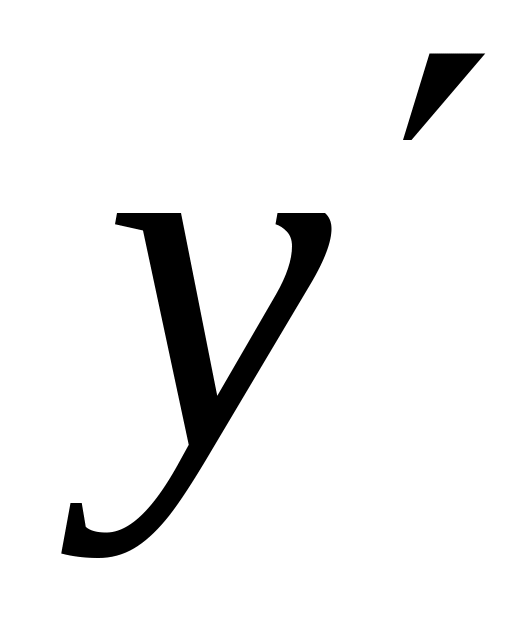и , если .

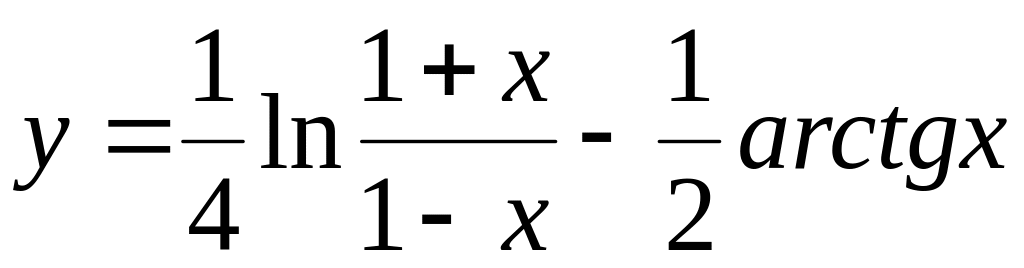Найти .

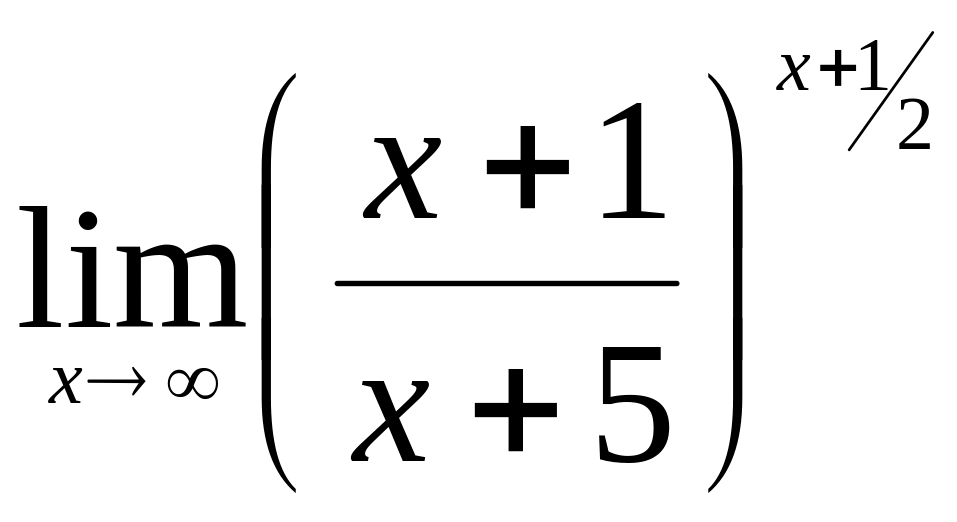Найти наибольшее и наименьшее значения функции .

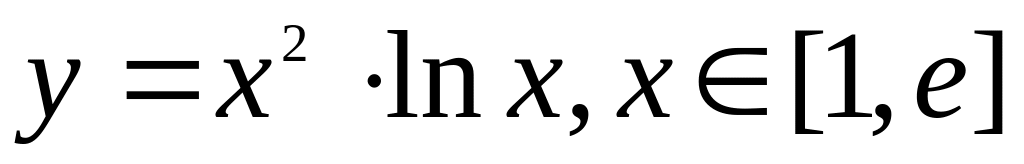Локальный экстремум функции (определения), первое достаточное условие существования локального экстремума функции.

Найти , если .

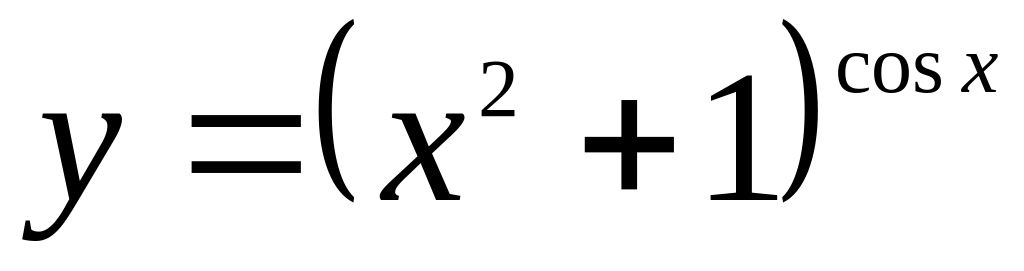Найти .

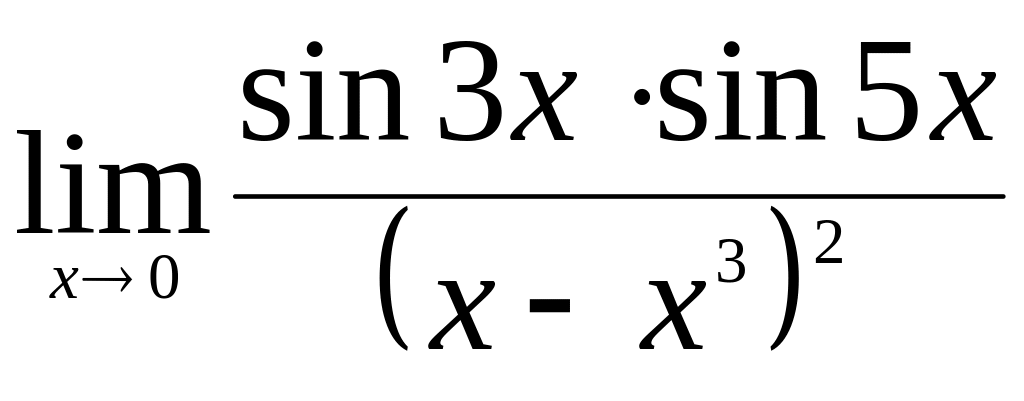Найти интервалы выпуклости и точки перегиба графика функции .

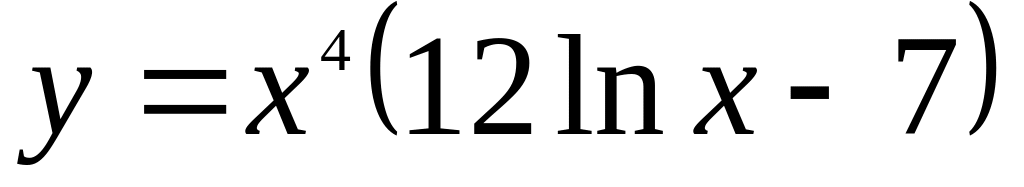Локальный экстремум функции (определения), второе достаточное условие существования экстремума функции.

Найт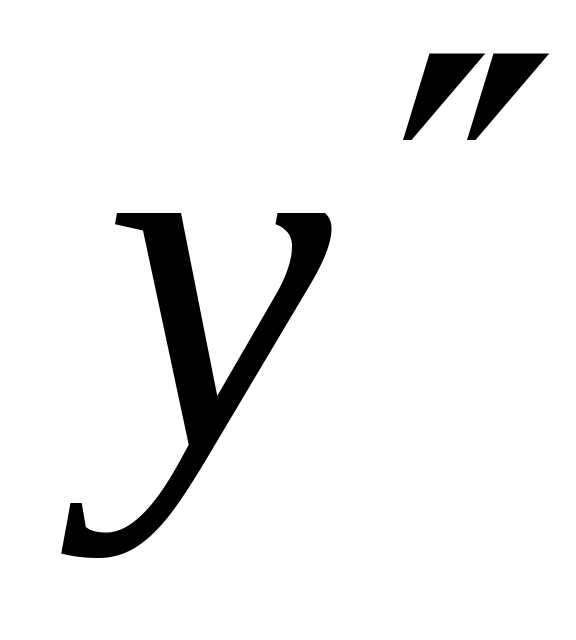и , если .

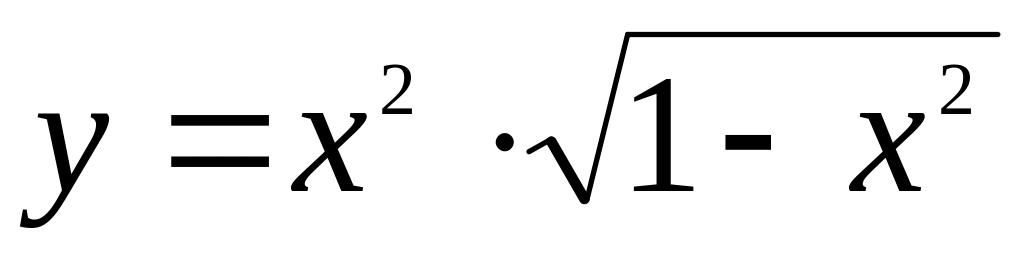Найти .

Найти наибольшее и наименьшее значения функции .

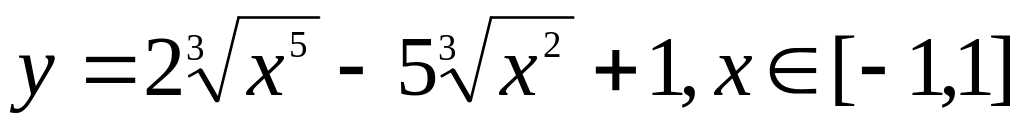Формула Тейлора-Маклорена и Тейлора для многочлена.

Найти , если .

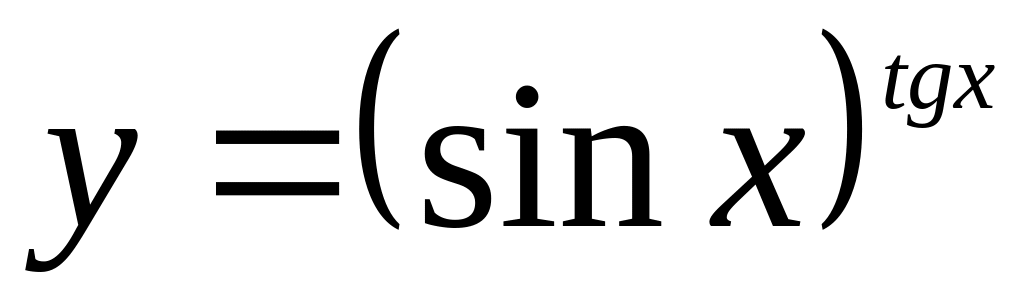Найти .

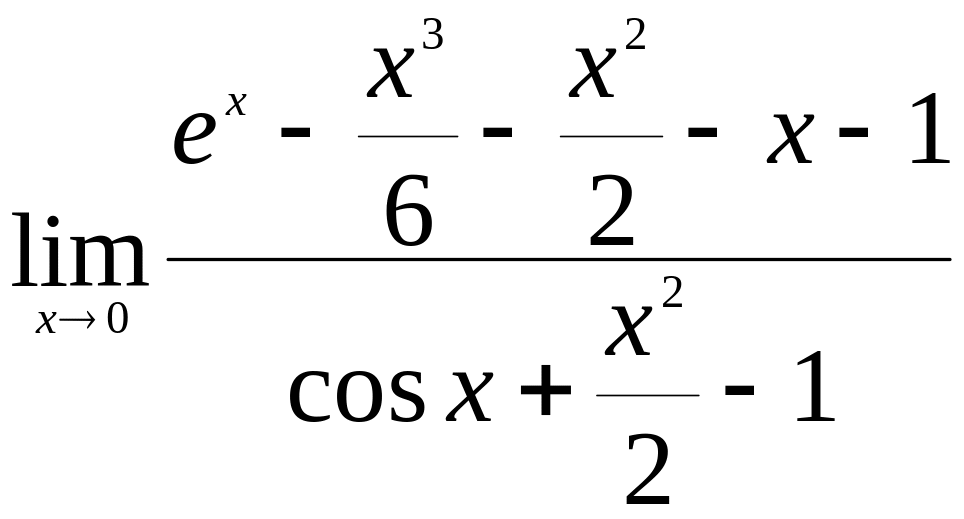Исследовать функцию на экстремум и найти интервалы монотонности: .

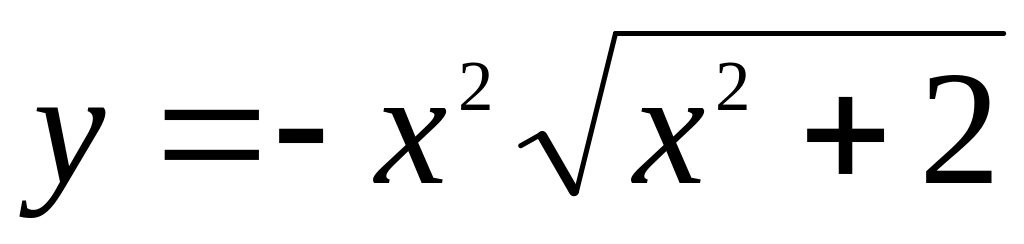Формула Бинома Ньютона, свойство биномиальных коэффициентов.

Найти , если .

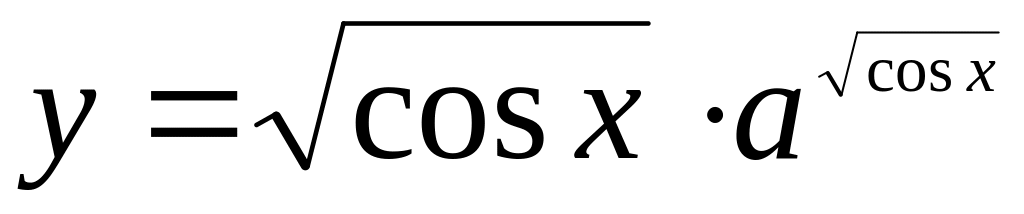Найти .

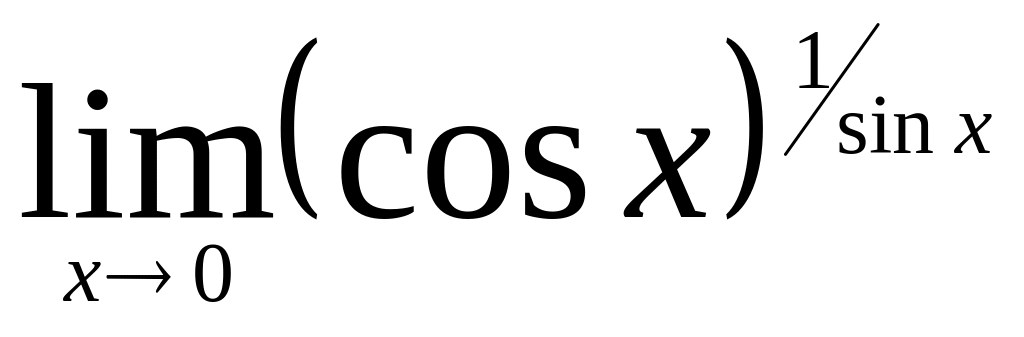Исследовать функции на экстремум и найти интервалы монотонности .

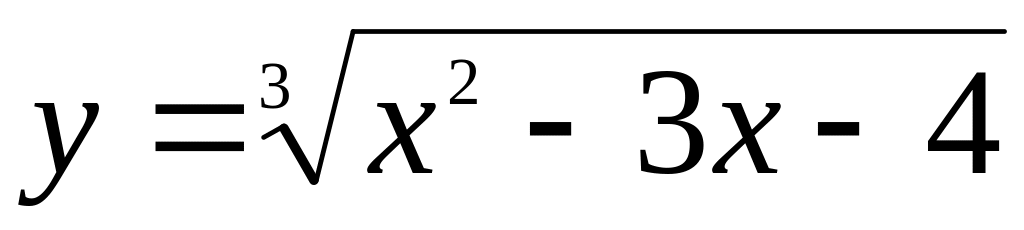Формула Тейлора-Маклорена и формула Тейлора для произвольной функции. Разложение по формуле Тейлора-Маклорена некоторых элементарных функции.

Найти , если .

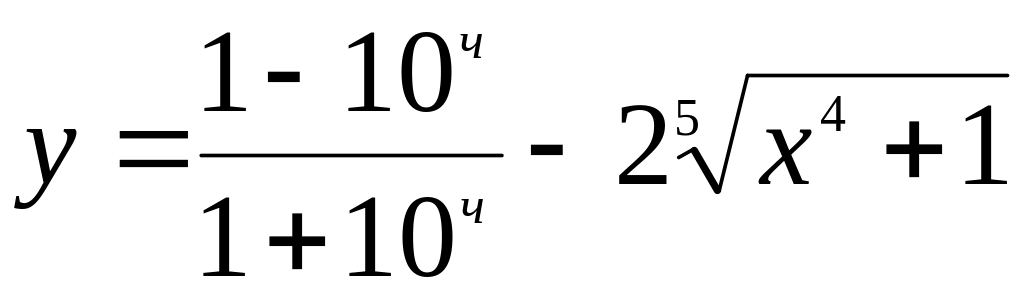Найти .

Исследовать функцию на экстремум и найти интервалы монотонности .
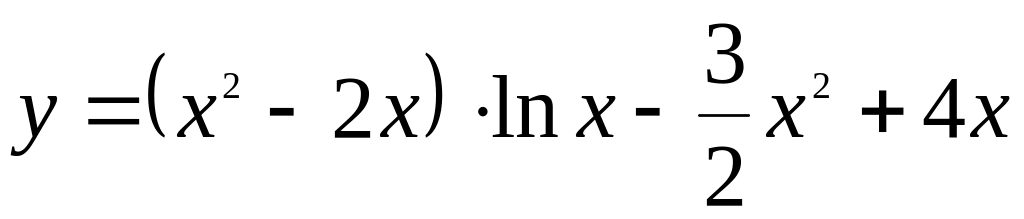