
- •Экзаменационный билет № 1 по математическому анализу
- •3. А) Вычислить ;
- •3. А) Исследовать на непрерывность функцию ;
- •А) Исследовать на непрерывность функцию ;
- •А) Вычислить ;
- •2. Теорема о связи дифференцируемости и непрерывности функции.
- •Эквивалентные функции. Теорема о замене функций на эквивалентные в произведении и в отношении (при вычислении пределов). Таблица эквивалентностей.
- •Понятие дифференцируемости функции в точке. Критерий дифференцируемости функции в точке.
- •А) Вычислить ;
- •Первый замечательный предел.
- •Первый замечательный предел: .
- •Правило Лопиталя.
Первый замечательный предел.
Теорема о существовании и непрерывности обратной функции.
Глобальный максимум и минимум функции и метод его вычисления.
Найти
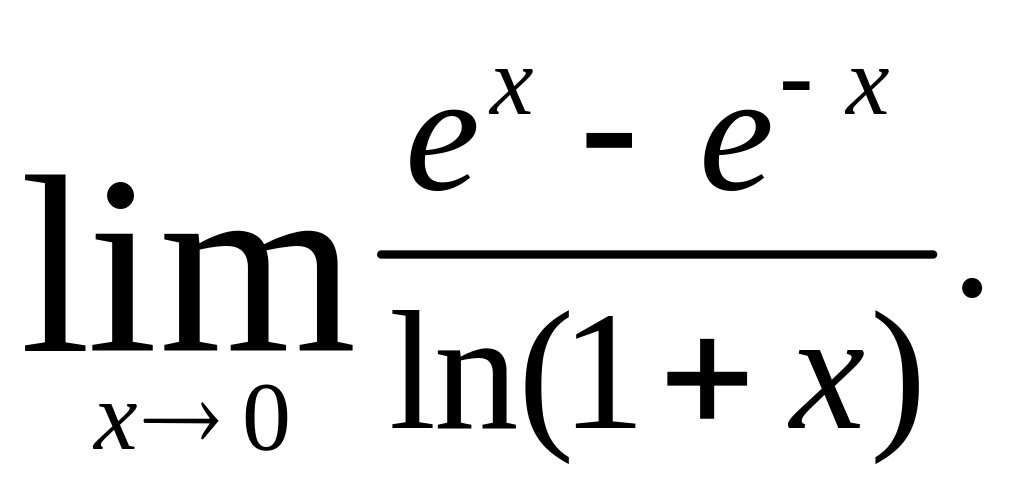
Исследовать на экстремум функцию
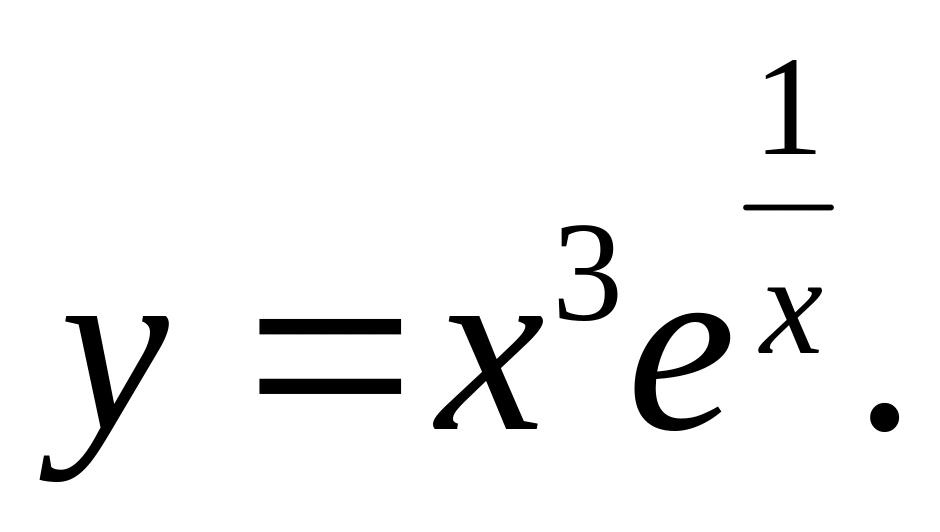
Вычислить

Свойства определенного интеграла, выражаемые равенствами.
Теорема о переходе к пределу в неравенстве и о трех пределах.
Достаточное условие выпуклости и точек перегиба.
Найти
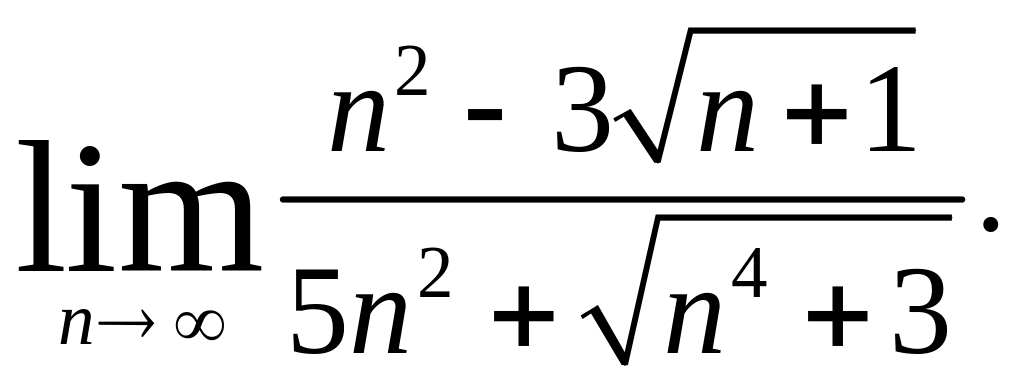
Найти если
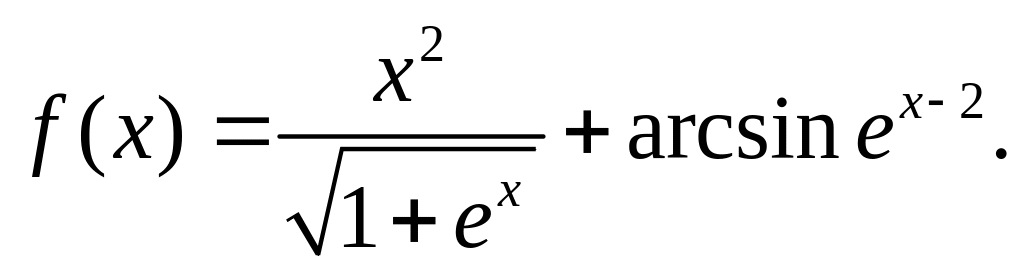
Найти

Теорема о среднем значении для определенного интеграла.
Понятие дифференциала функции. Критерий дифференцируемости функции.
Понятия выпуклой функции и точек перегиба.
Найти

Исследовать функцию
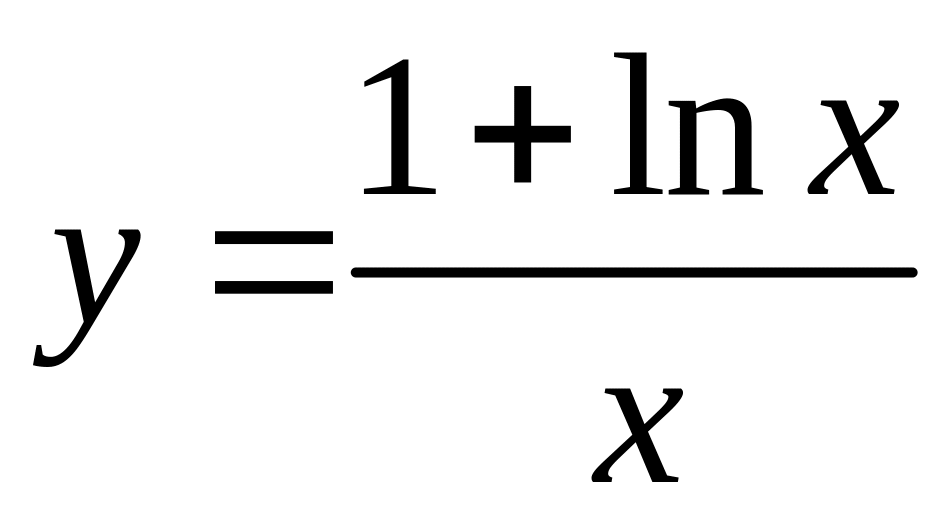 на экстремум и указать интервалы
монотонности.
на экстремум и указать интервалы
монотонности.Найти
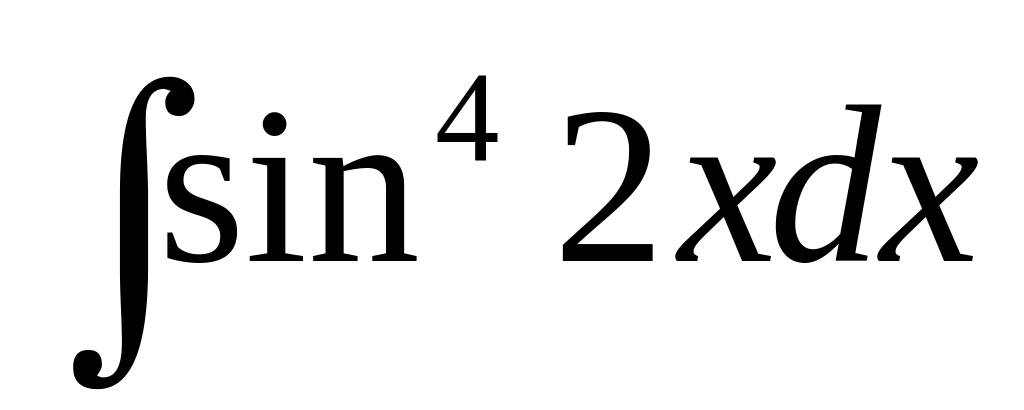
Бесконечно малые функции, их свойства.
Найти
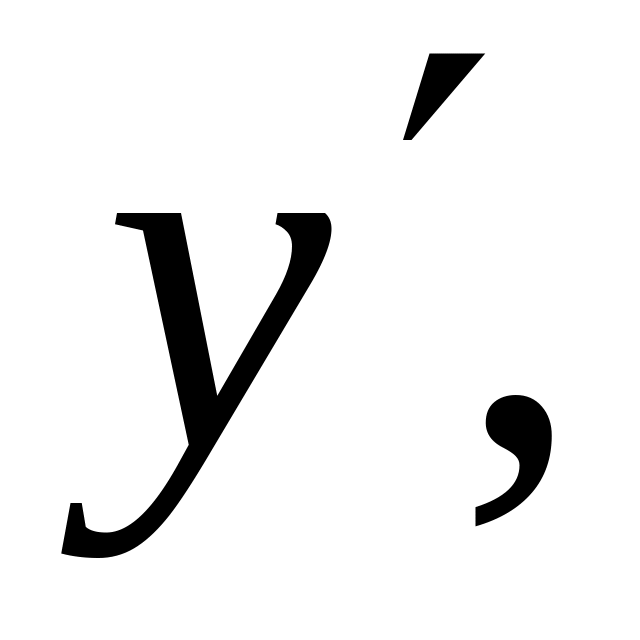 если
если
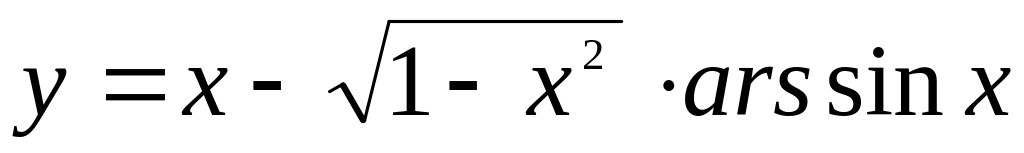 .
.Найти
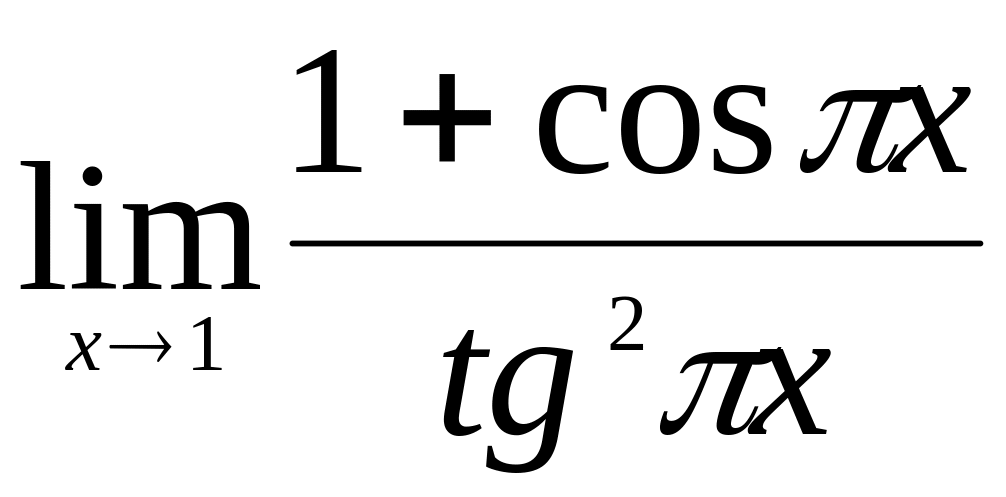 .
.Найти интервалы монотонности и исследовать функцию на экстремум
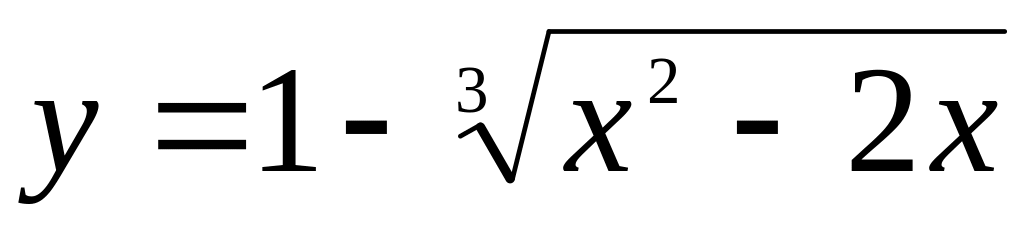 .
.
Определение предела функции на языке окрестностей, критерий существования конечного предела функции.
Найти если
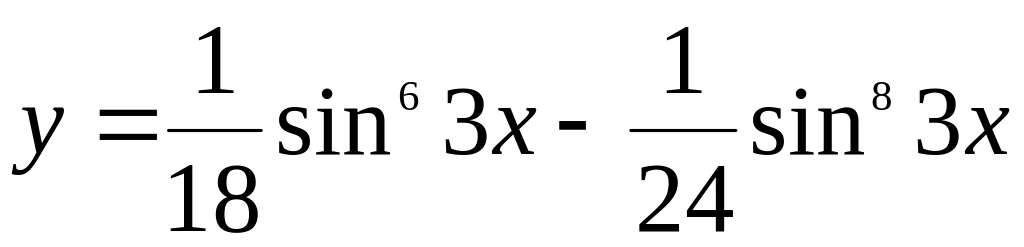 .
.Найти
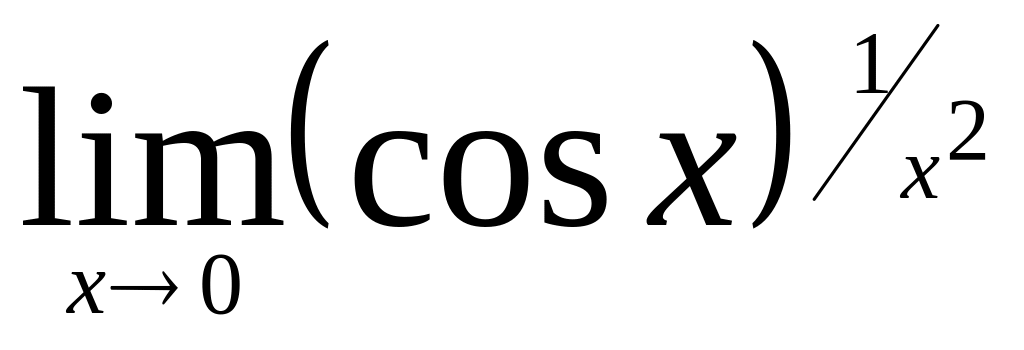 .
.Указать точки перегиба и направление выпуклости
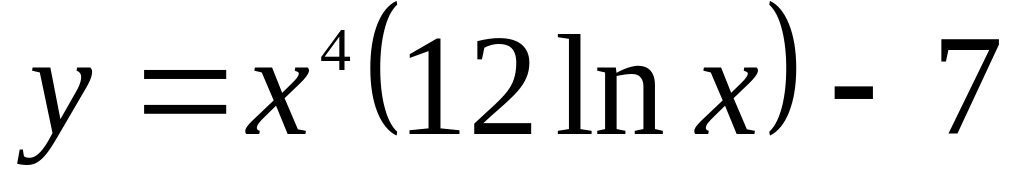 .
.
Определение предела функций на языке неравенств, теорема о пределе суммы, разности, произведения и частного функций.
Найти
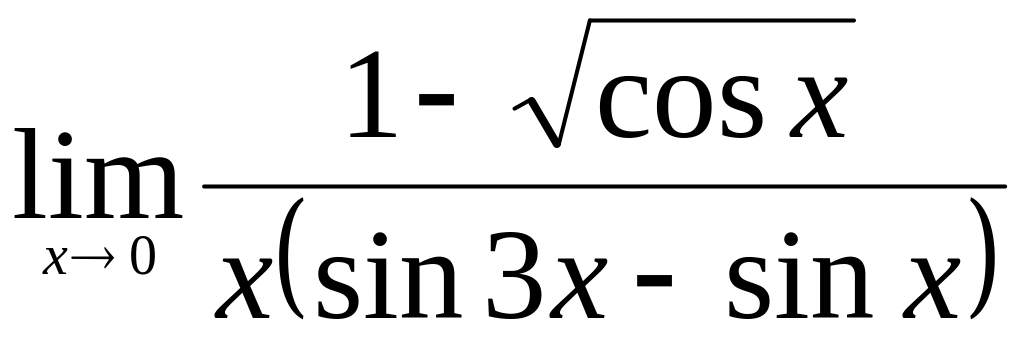 .
.Найти если
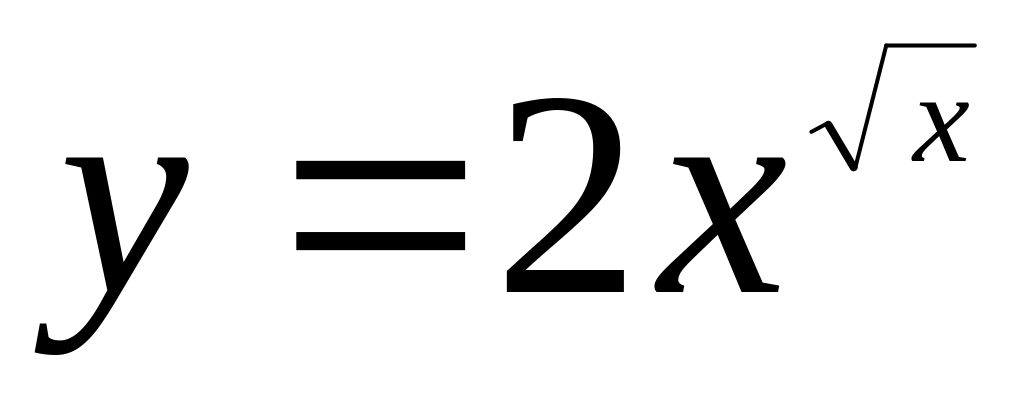 .
.Исследовать функцию на экстремум и найти интервалы монотонности:
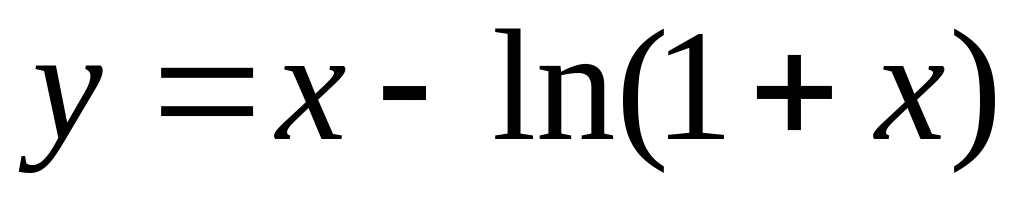 .
.
Бесконечно большие функции и их свойства. Связь бесконечно больших и бесконечно малых функций.
Найти
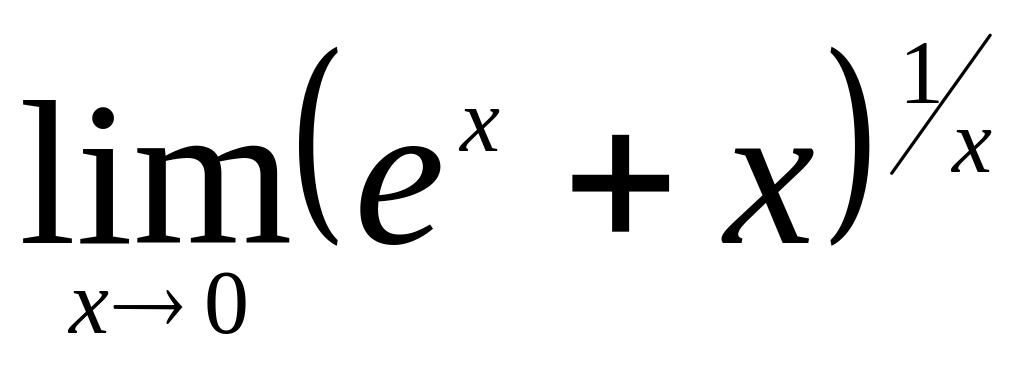 .
.Найти если
 .
.Исследовать функцию на экстремум и найти промежутки монотонности
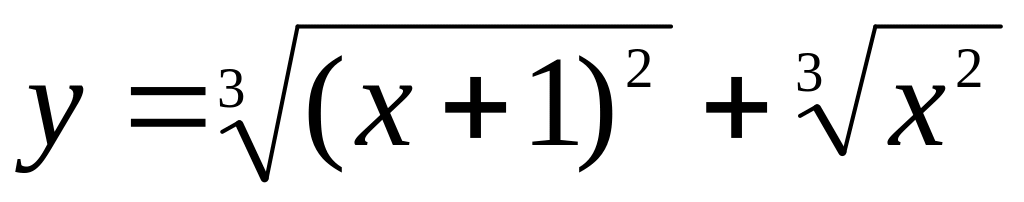 .
.
Первый замечательный предел: .
Найти
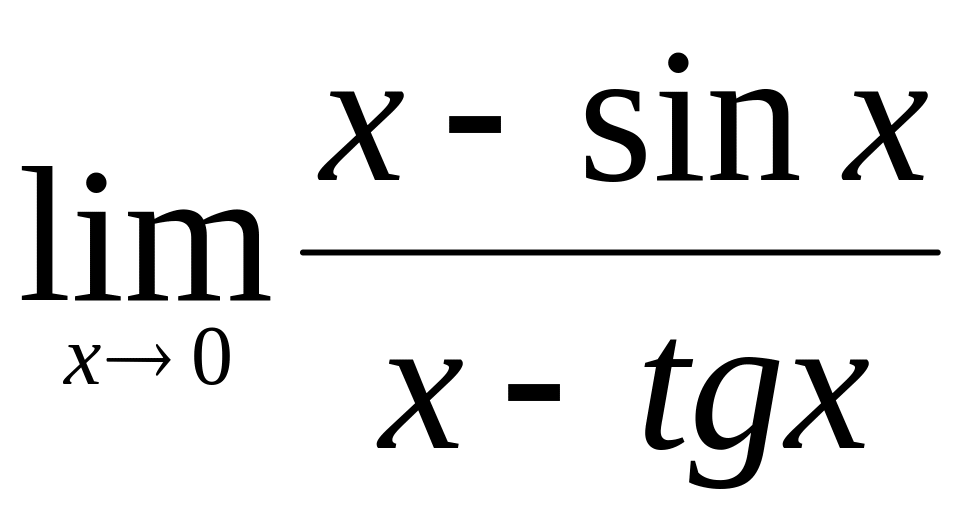 .
.Найти если
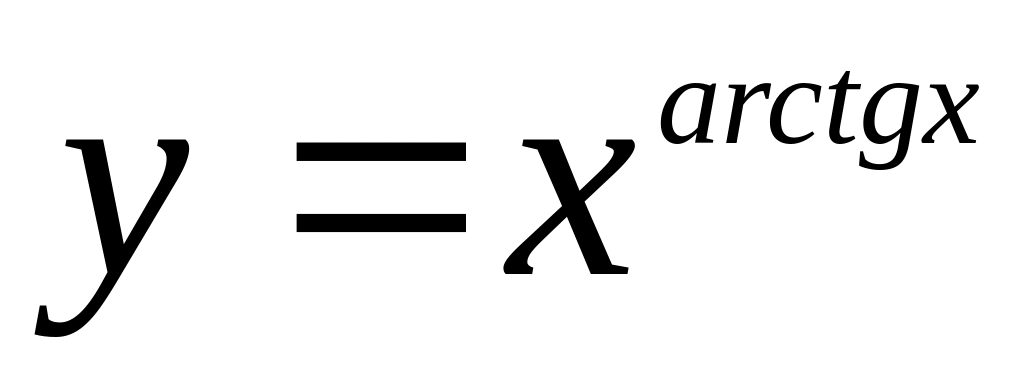 .
.Найти интервалы выпуклости и точки перегиба графика функции
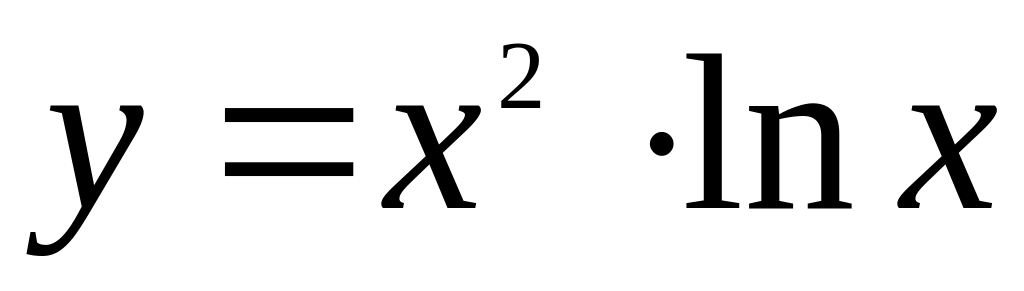 .
.
Непрерывность функции в точке. Теорема об арифметических операциях над непрерывными функциями
Найти если
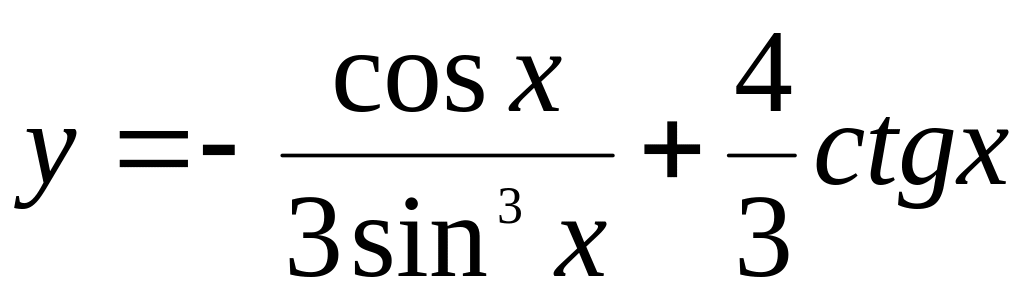 .
.Найти
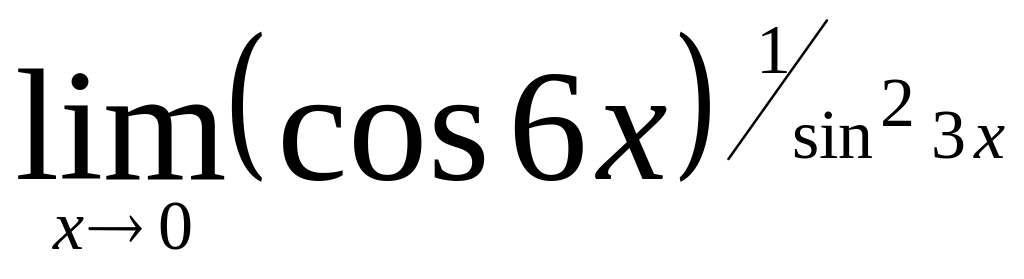 .
.Найти интервалы выпуклости и точки перегиба графика функции
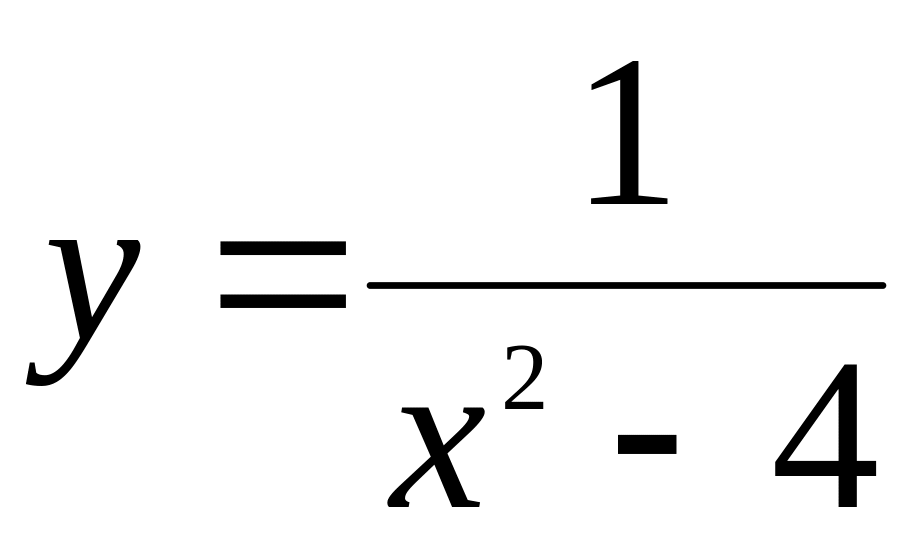 .
.
Непрерывность функции в точке. Доказать непрерывность функций:
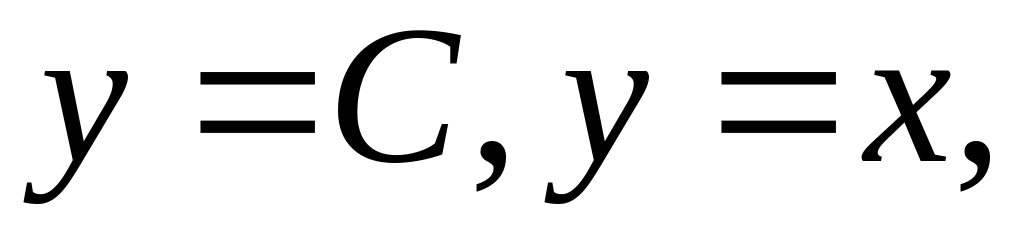 целой
и дробно рациональной функций в их
областях определений.
целой
и дробно рациональной функций в их
областях определений.Найти если
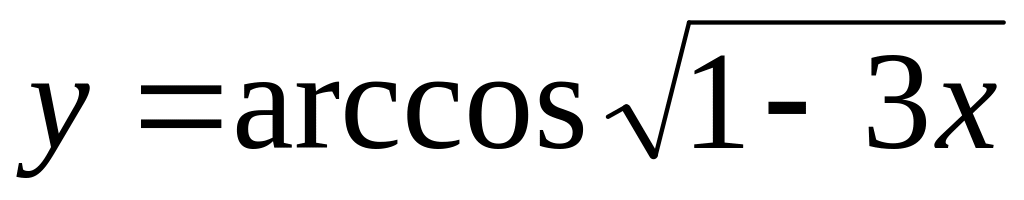 .
.Найти
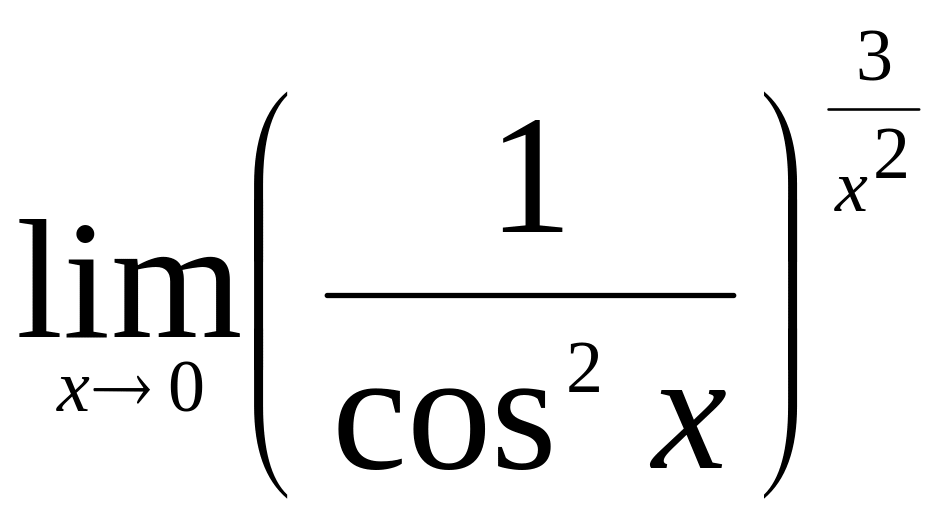 .
.Найти интервалы выпуклости и точки перегиба графика функции
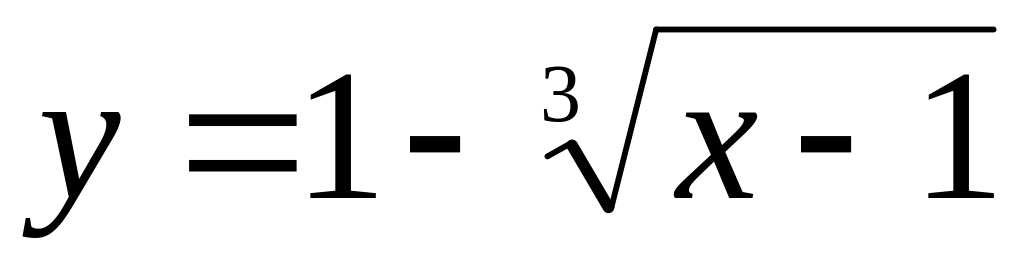 .
.
Доказать непрерывность функции
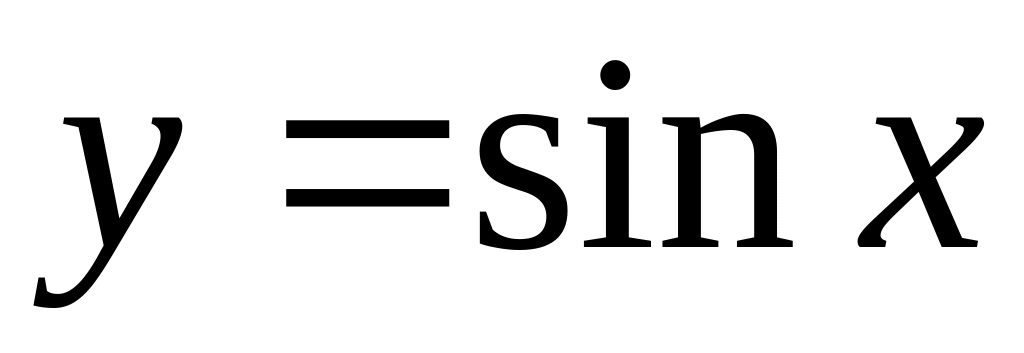 на множестве
на множестве
 .
Точки разрыва функции, их классификация.
.
Точки разрыва функции, их классификация.Найти если
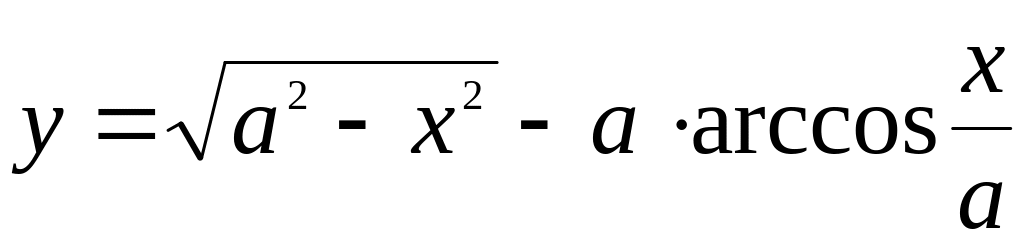 .
.Найти
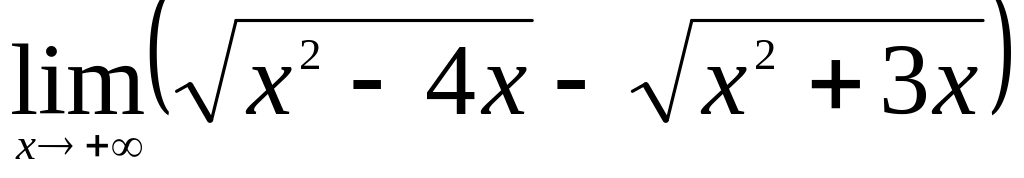 .
.Найти асимптоты графика функции
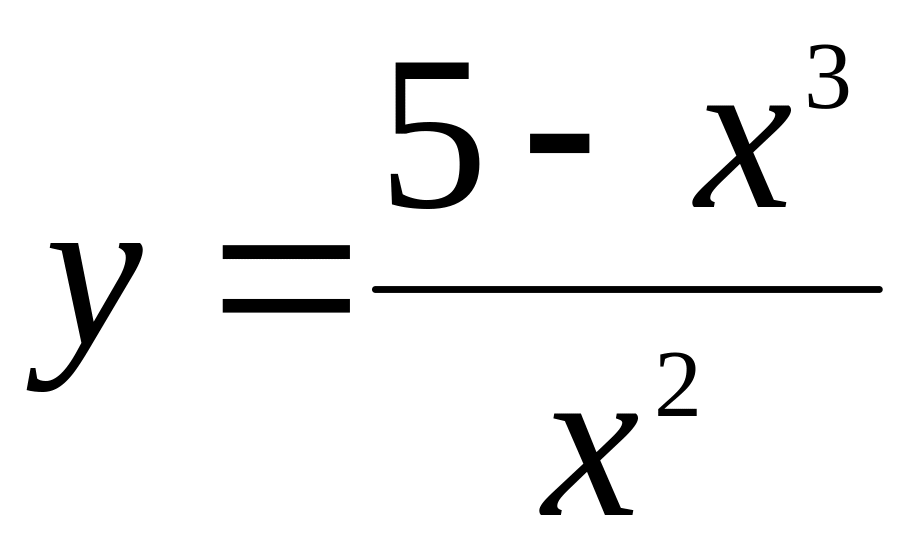 .
.
Производная функции в точке. Геометрический смысл производной. Вывод формул производных функций
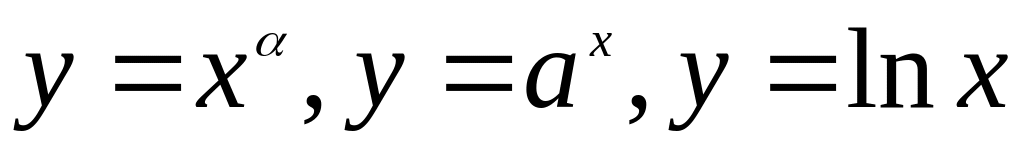 .
.Найти
 если
если
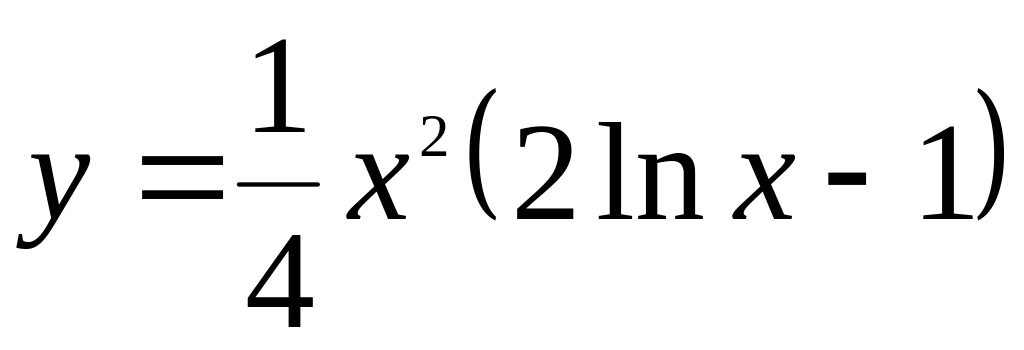 .
.Найти
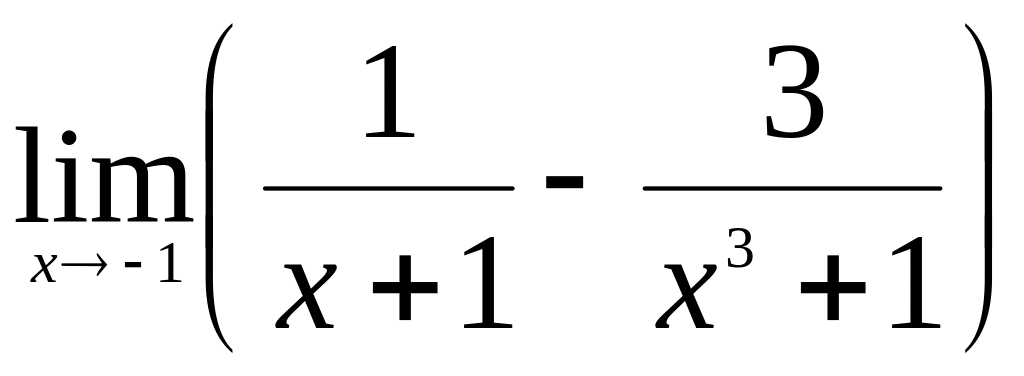 .
.Найти интервалы монотонности функции
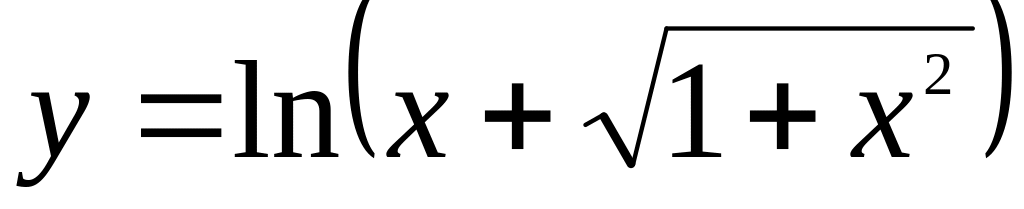 .
.
Производная функции в точке. Вывод формул производных функций
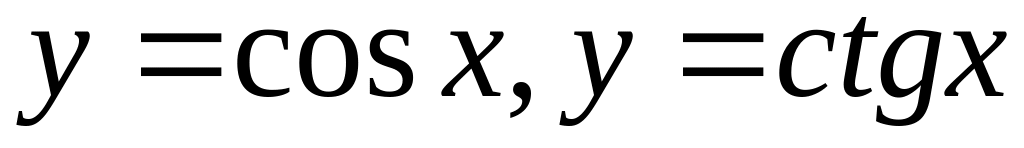 .
Механический смысл производной.
.
Механический смысл производной.Найти если
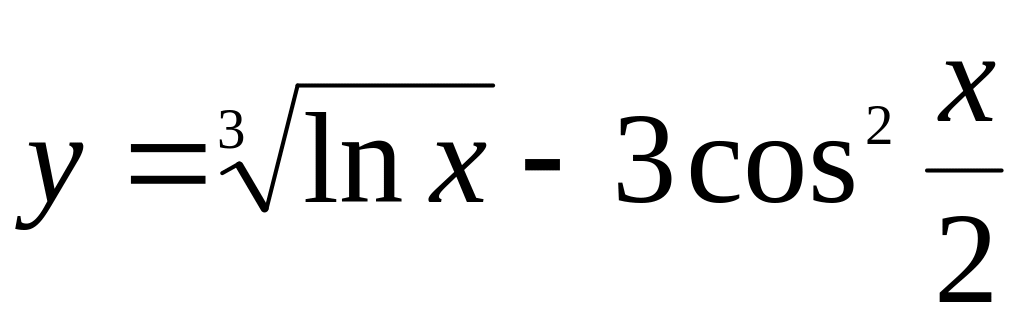 .
.Найти
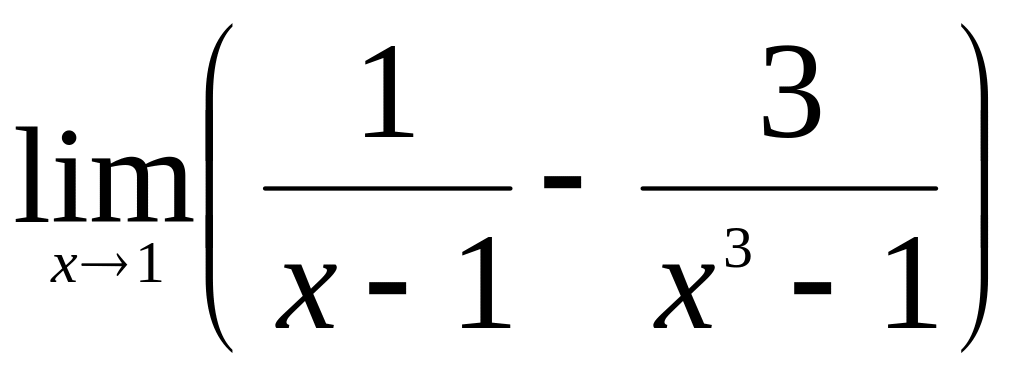 .
.Найти интервалы выпуклости и точки перегиба графика функции
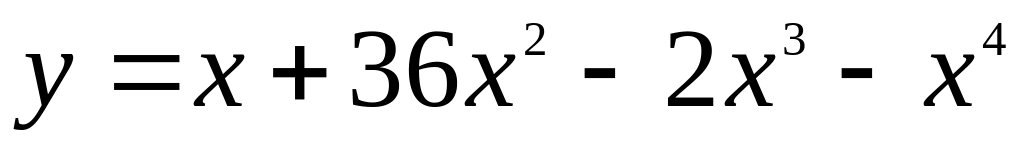 .
.
Теорема о производной от обратной функции.
Найти если
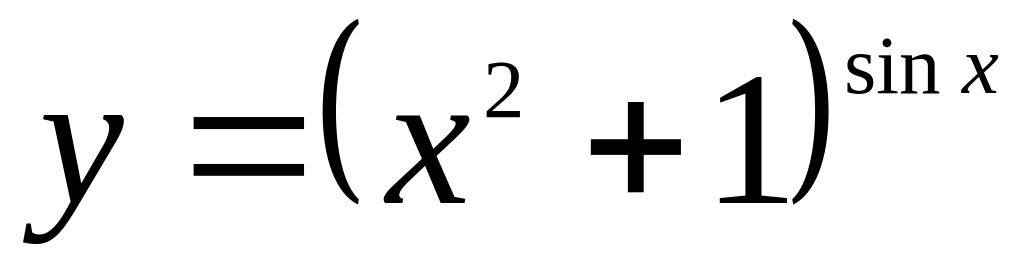 .
.Найти
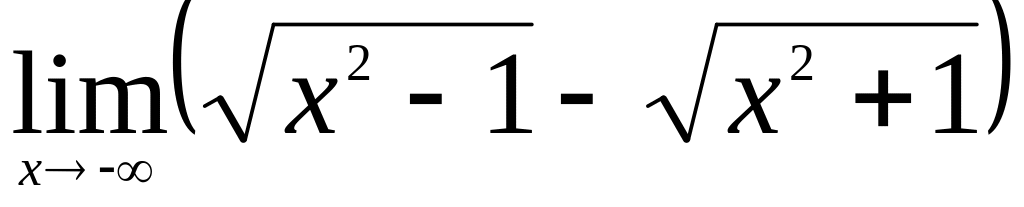 .
.Найти асимптоты графика функции
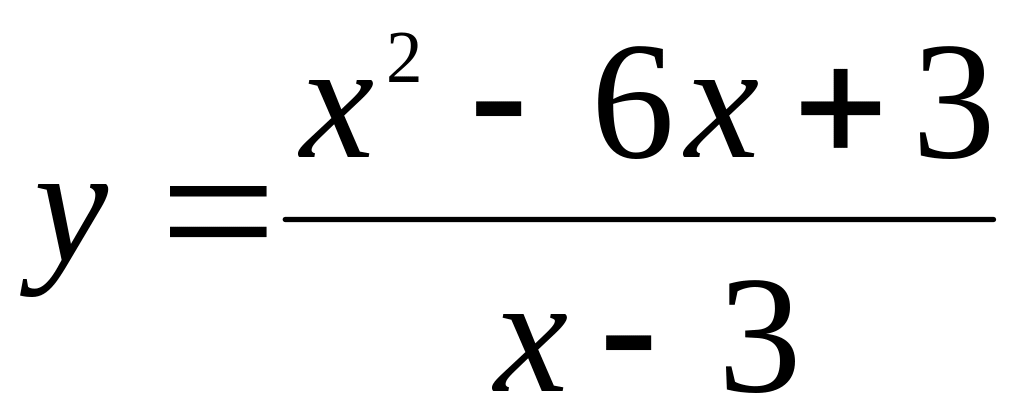 .
.
Определение обратной функции. Вывод формул производных от функций
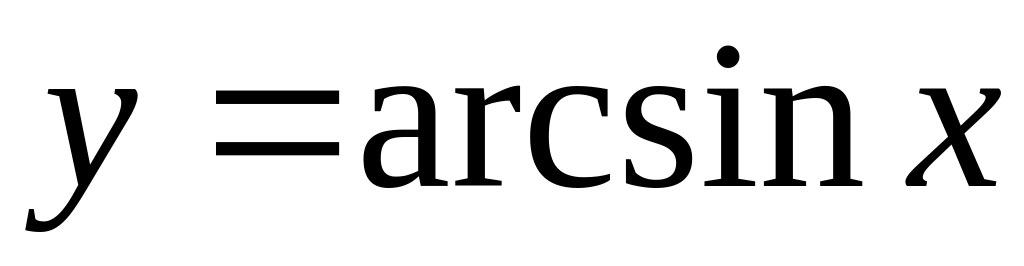 и
и
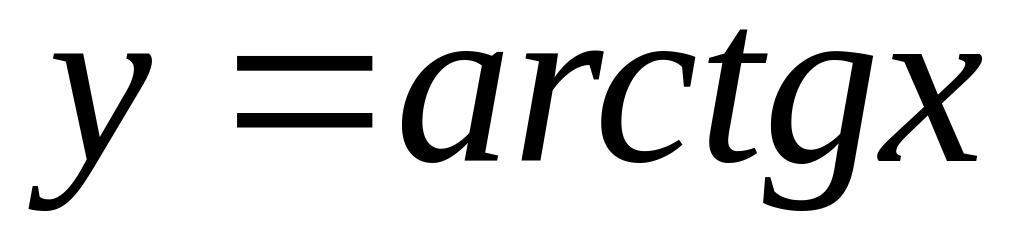 .
.Найти
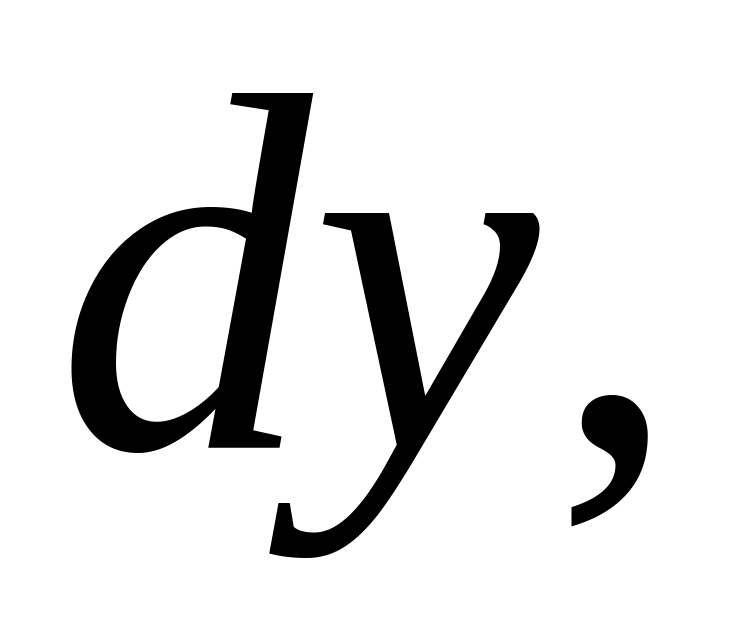 если
если
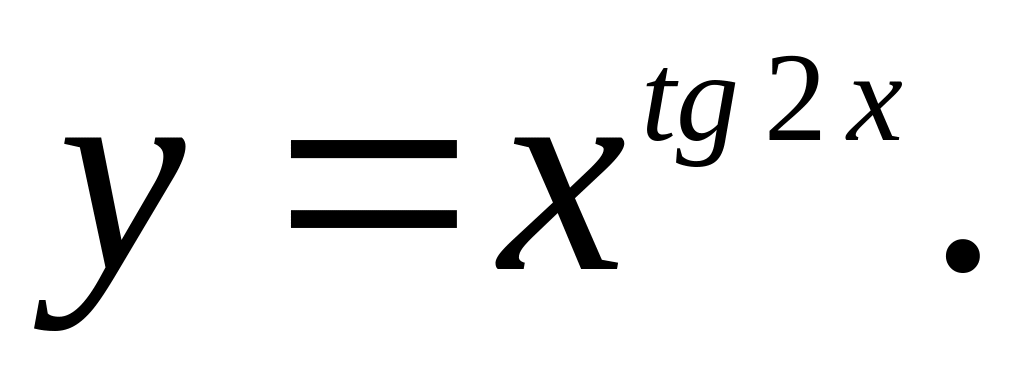 .
.Найти
 .
.Исследовать функцию на экстремум и найти интервалы монотонности:
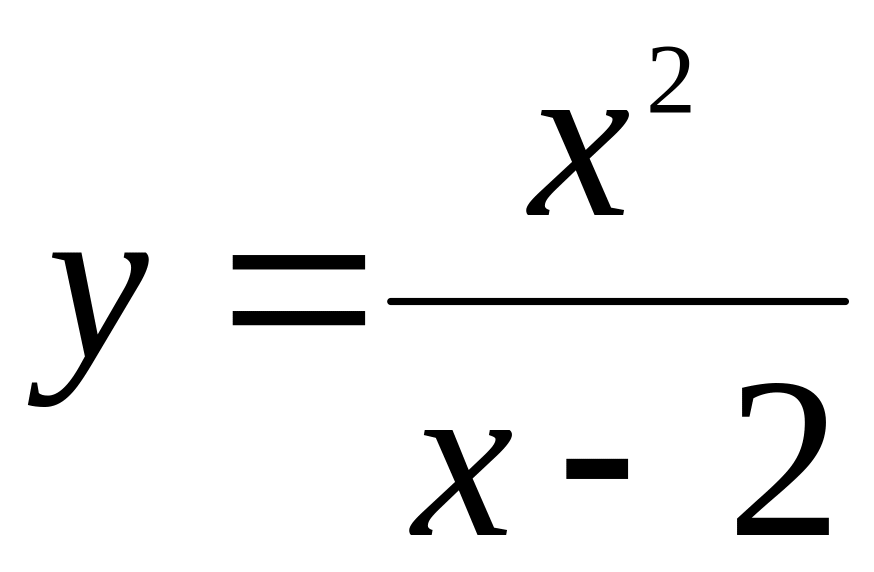 .
.
Теорема о приращении дифференцируемой функции в точке, следствие.
Найти если
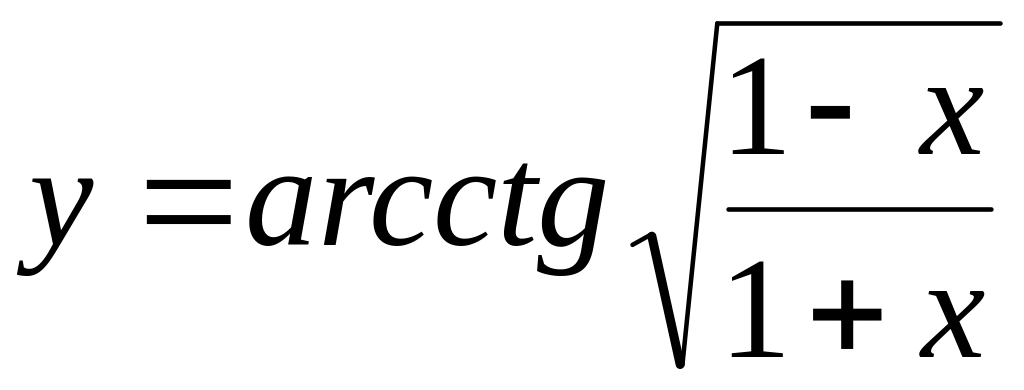 .
.Найти
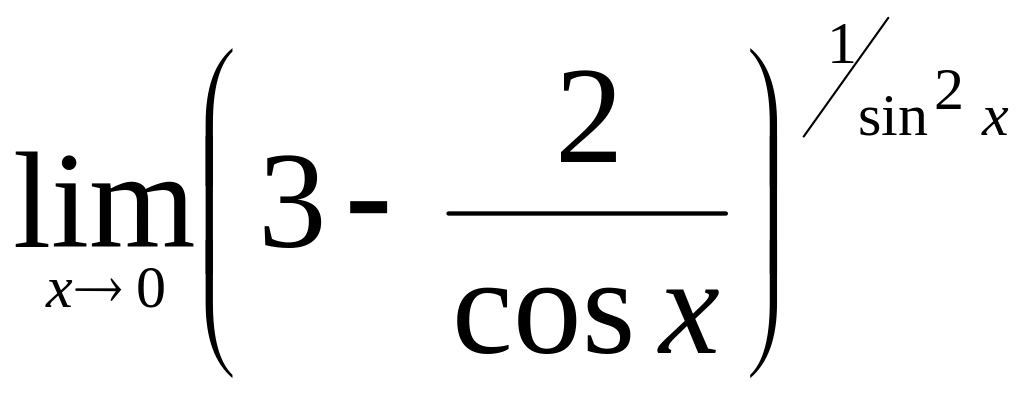 .
.Исследовать функцию на экстремум и найти интервалы монотонности
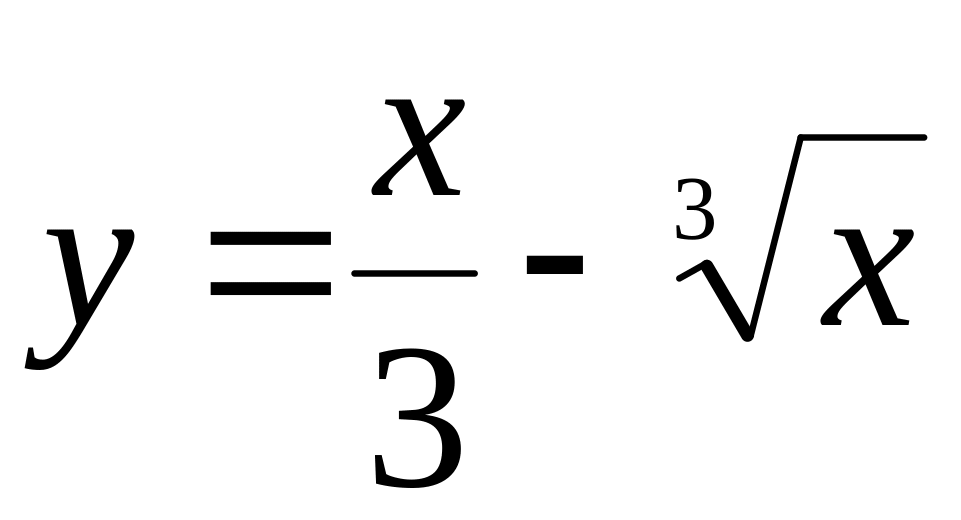 .
.
Теорема о производной от суперпозиции функций
Найти если
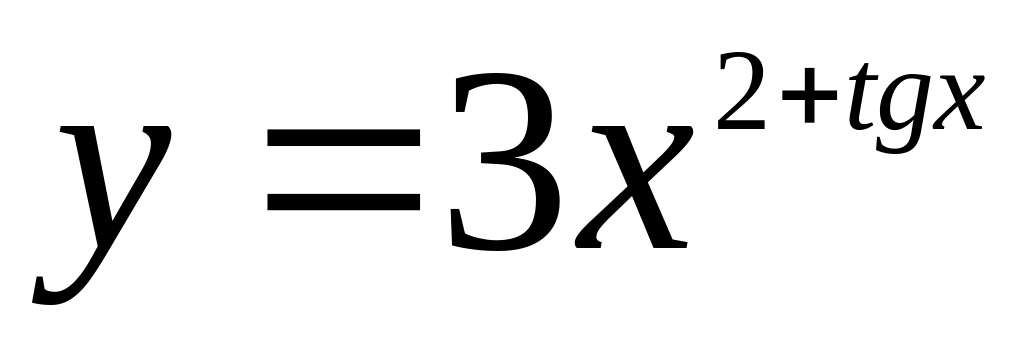 .
.Найти
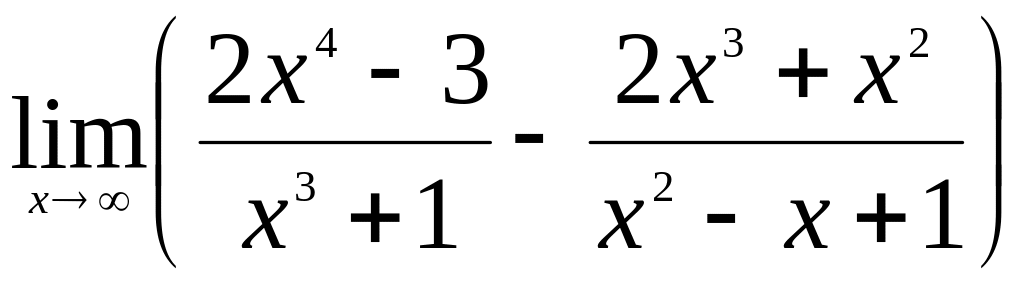 .
.Найти интервалы выпуклости и точки перегиба графика функции
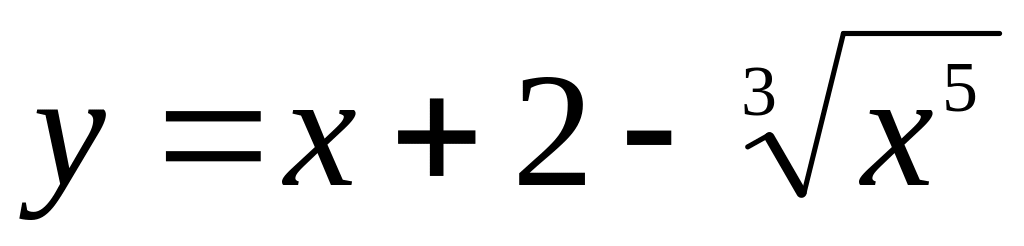 .
.
Теорема о производной от алгебраической суммы, произведения и частного.
Найти если
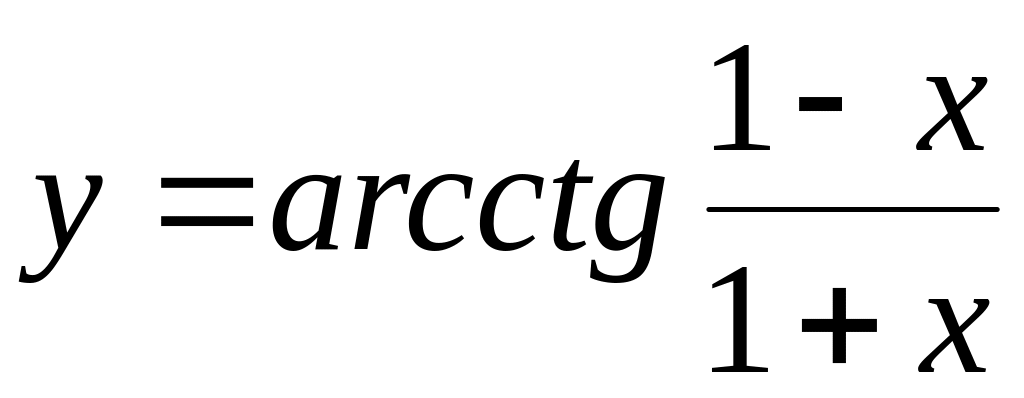 .
.Найти
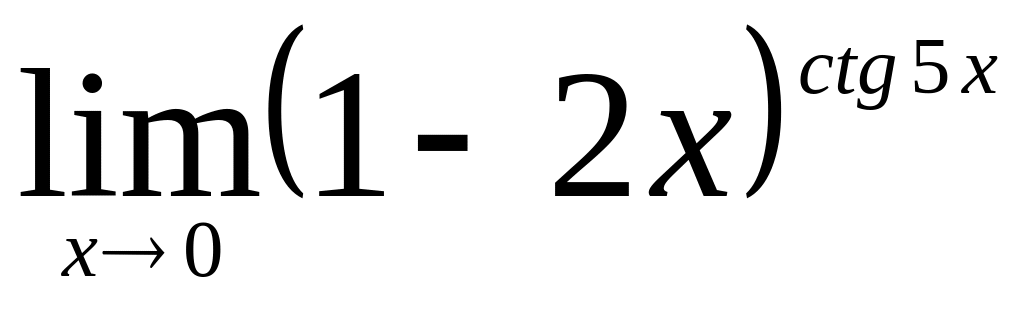 .
.Найти асимптоты графика функции
 .
.
Дифференциал функции в точке. Применение дифференциала для приближенных вычислений .
Найти если
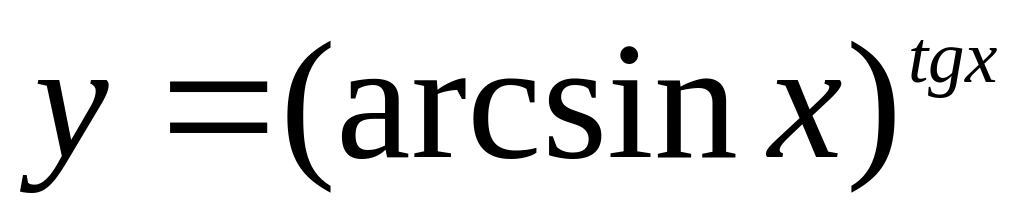 .
.Найти
 .
.Исследовать функцию на экстремум и найти интервалы монотонности
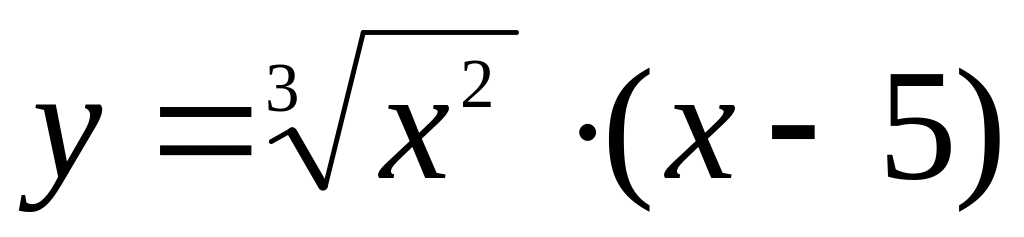 .
.
Параметрическое задание функции. Производная от функции, заданной в параметрическом виде.
Найти если
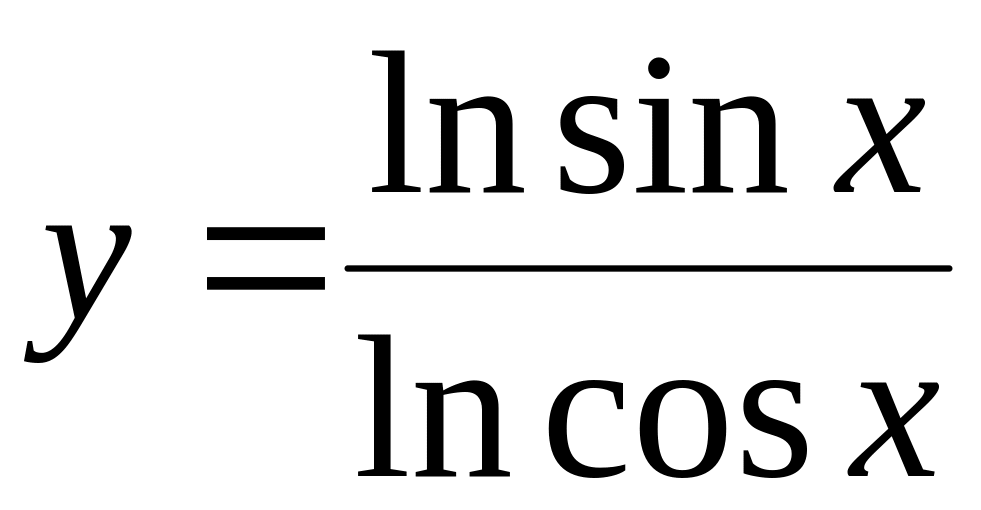 .
.Найти
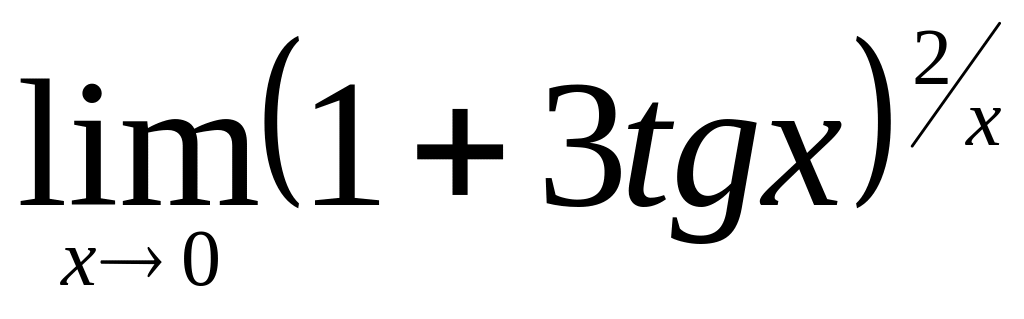 .
.Исследовать функцию на экстремум и найти промежутки монотонности
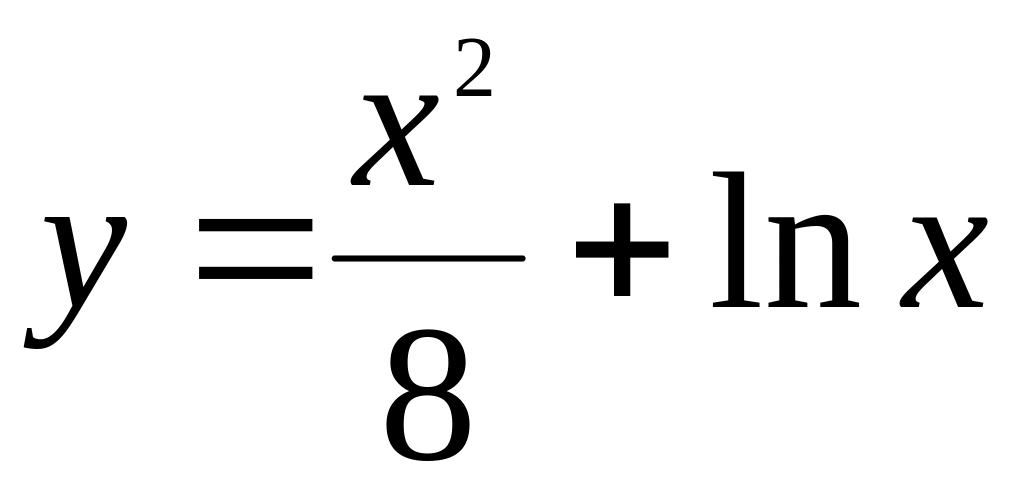 .
.
Дифференциал функции в точке, инвариантность вида дифференциала.
Найти если
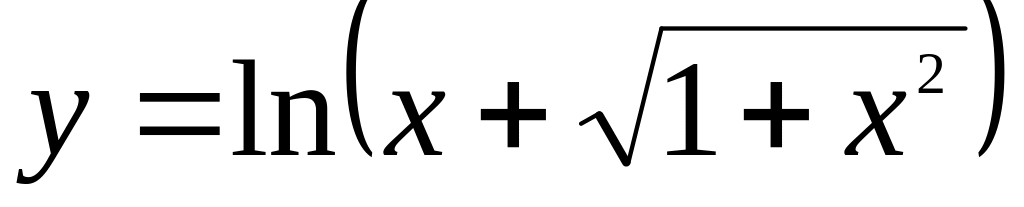 .
.Найти
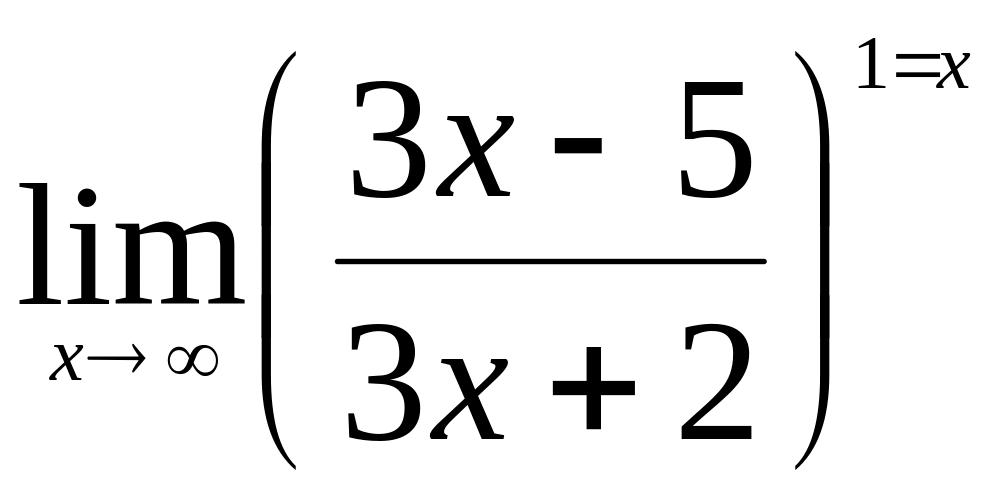 .
.Исследовать функцию на экстремум и найти промежутки монотонности
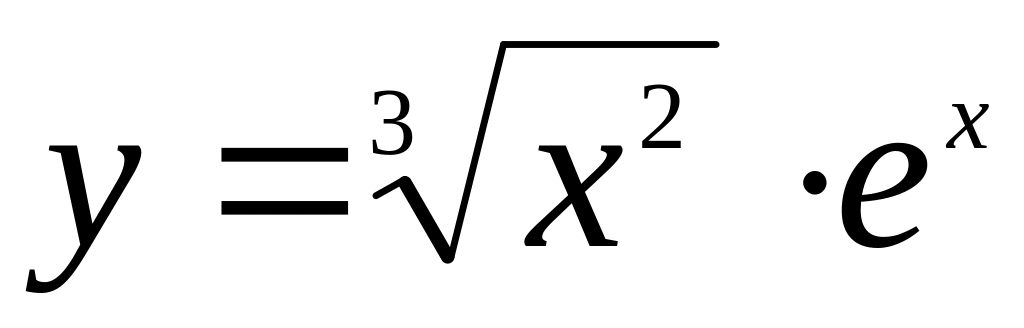 .
.
