Экзаменационный билет № 1 по математическому анализу

1. Теорема об ограниченности функции, имеющей конечный предел.

2. Критерий монотонности функции.

3. а) Вычислить ;

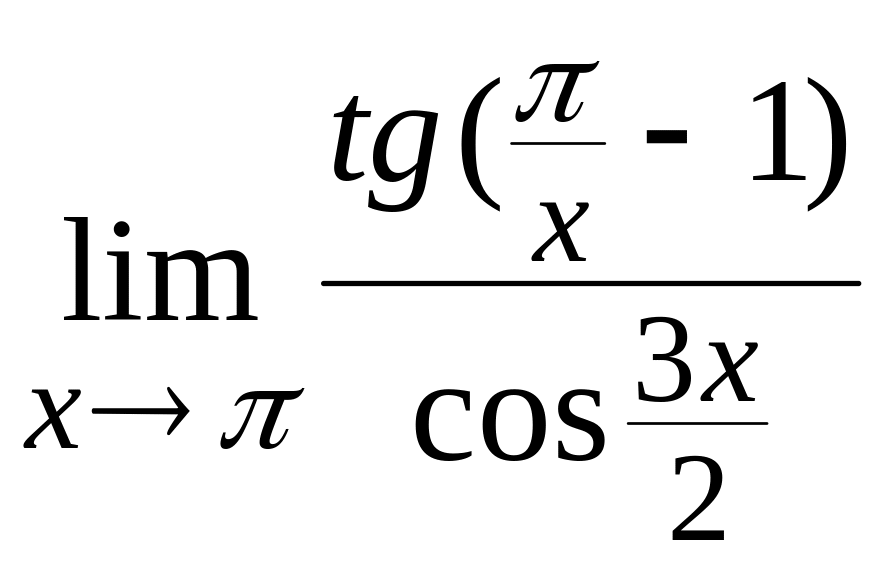б) Найти интервалы выпуклости и точки перегиба: ;

в) Найти , если .

1. Бесконечно малые функции и их свойства.

2. Теорема Лагранжа. Теорема Ролля и ее геометрический смысл.

3. а) Вычислить, используя правило Лопиталя ;

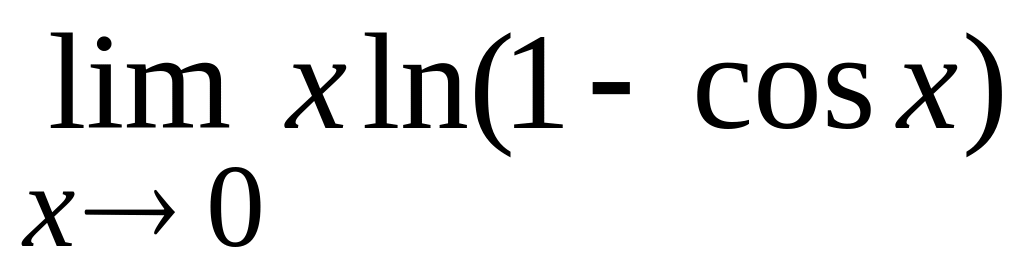б) Найти дифференциал функции в точке x₀:

;

в) Исследовать на непрерывность функцию .

1. Теорема об арифметических операциях с пределами функций.

2. Критерий постоянства функции.

3. а) Вычислить, используя правило Лопиталя ;

б) Найти промежутки выпуклости и точки перегиба ;

в) Найти все асимптоты графика функции .

1. Теорема о связи между бесконечно малыми и бесконечно большими функциями.

2. Правило Лопиталя.

3. а) Исследовать на непрерывность функцию ;

б) Найти производную функции ;

в) Вычислить: .

1. Первый замечательный предел.

2. Дифференциал первого порядка. Инвариантность формы дифференциала первого порядка.

3. а) Найти все асимптоты графика функции ;

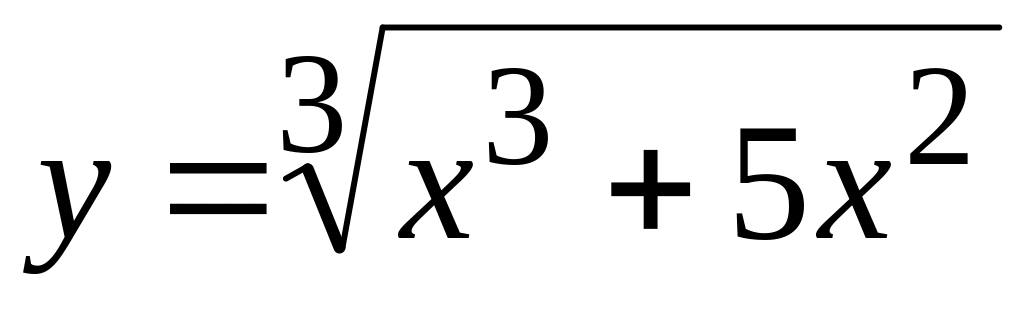б) Найти вторую производную функции ;

в) Вычислить: .

1. Определения непрерывности функции. Доказательство непрерывности по определению функций: .

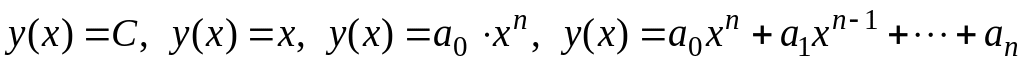2. Теорема об арифметических операциях с дифференцируемыми функциями, следствие.

3. а) Найти производную функции ;

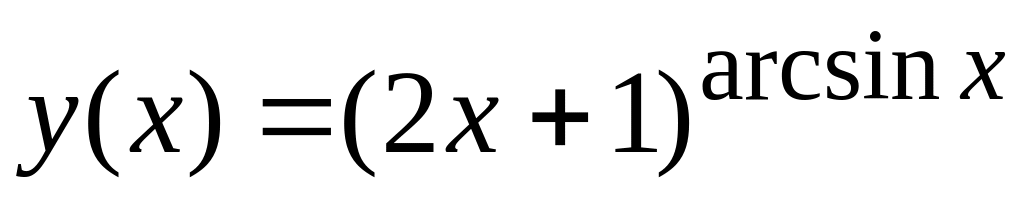б) Вычислить ;

в) Найти интервалы монотонности и точки экстремума функции .

1. Критерий существования у функции конечного предела.

2. Понятие производной функции в точке. Вывести производные функций: .

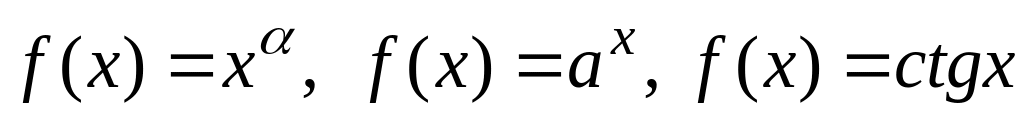3. А) Вычислить ;

б) Найти дифференциал функции ;

в) Найти интервалы монотонности и точки экстремума .

1. Бесконечно большие функции (б.б.ф.) и их свойства (б/д). Теорема о связи между бесконечно малыми и бесконечно большими функциями.

2. Понятие производной функции. Вывести производные функций: .

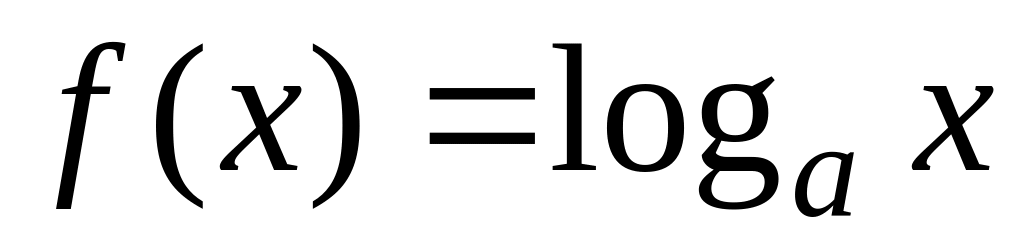3. а) Найти асимптоты графика функции ;

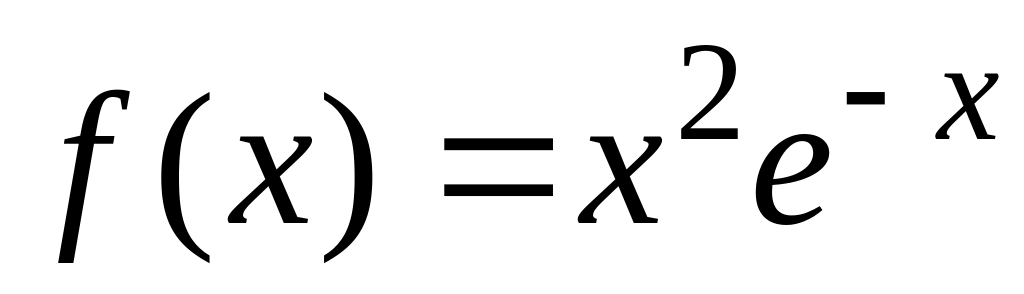б) Найти производную функции ;

в) Вычислить: .

1. Точки разрыва и их классификация.

2. Понятие точки локального экстремума. Достаточные условия локального экстремума.

3. А) Исследовать на непрерывность функцию ;

б) Найти наибольшее и наименьшее значение функции

на [-1; 1];

в) Найти дифференциал функции в точке .

1. Теорема об арифметических операциях с непрерывными функциями.

2. Необходимое условие экстремума. Примеры, показывающие, что приведенное в теореме условие не является достаточным.

3. А) Исследовать на непрерывность функцию ;

б) Найти интервалы выпуклости и точки перегиба: ;

в) Вычислить, используя правило Лопиталя .

1. Теорема о единственности предела.