
- •1. Определение и виды матриц. Транспонированная матрица. Сложение матриц. Умножение матрицы на число. Линейная зависимость и независимость столбцов и строк матрицы. Умножение матриц и его свойства.
- •2. Определители II и III порядков. Определитель матрицы n-ro порядка. Свойства определителей. Алгебраическое дополнение. Вычисление обратной матрицы с помощью определителя.
- •4. Ранги матриц. Теорема Кронекера-Капелли. Однородная система линейных уравнений. Структура общего решения системы линейных уравнений.
- •8. Инвариантные подпространства. Собственные подпространства. Характеристическое уравнение. Свойства характеристическом многочлена. Приведение матрицы преобразования к диагональному виду.
- •9. Определение вектора и операции над ними. Свойства операций над векторами. Линейная зависимость векторов. Геометрический смысл линейной зависимости. Базис.
- •10. Скалярное произведение векторов. Свойства скалярного произведения векторов. Длины векторов и углы между ними. Скалярное произведение векторов в координатной форме. Матрица Грама.
- •12. Уравнения линий и поверхностей. Полярная система координат. Прямая линия на плоскости. Различные виды уравнений. Взаимное расположение прямых.
- •13. Уравнения плоскостей и прямых в пространстве.
- •14. Линии второго порядка. Эллипс. Гипербола. Канонические уравнение. Фокальные расстояния. Эксцентриситеты.
- •15. Парабола. Директриса параболы. Каноническое уравнение. Полярное уравнение кривых второго порядка. Общее свойство кривых второго порядка.
- •18. Конус второго порядка. Параболоид. Однополостной и двуполостной гиперболоиды. Гиперболический параболоид
- •19. Преобразования плоскости. Линейные отображения. Аффинные отображения. Произведение отображений. Аффинные преобразования (операторы). Ортогональные преобразования.
15. Парабола. Директриса параболы. Каноническое уравнение. Полярное уравнение кривых второго порядка. Общее свойство кривых второго порядка.
Парабола: Линия, которая в некоторой декартовой прямоугольной системе координат может быть задана уравнением y2=2px называется параболой, а уравнение каноническим. Фокус – (p\2,0), директриса –прямая x=-p\2.
Р асстояние
от произвольной точки параболы до фокуса
равно r=x+p\2.
Для того чтобы точка M
лежала на параболе, необходимо и
достаточно, чтобы она была одинаково
удалена от фокуса и от директрисы этой
параболы.
Полярное уравнение кривых второго
порядка: Переход
к полярной системе осуществляется с
помощью формул r=корень
второй степени из x2+y2
φ=arctg(y\x),
а обратный формулами x=rcosφ
y=rsinφ.
асстояние
от произвольной точки параболы до фокуса
равно r=x+p\2.
Для того чтобы точка M
лежала на параболе, необходимо и
достаточно, чтобы она была одинаково
удалена от фокуса и от директрисы этой
параболы.
Полярное уравнение кривых второго
порядка: Переход
к полярной системе осуществляется с
помощью формул r=корень
второй степени из x2+y2
φ=arctg(y\x),
а обратный формулами x=rcosφ
y=rsinφ.
16. Общее уравнение кривой второго порядка. Пересечение с прямой. Асимптотические направление. Классификация уравнений второго порядка по их числу.
Общее уравнение кривой второго порядка: Ax2+2Bxy+Cy2+2Dx+2Ey+F=0
Пересечение
с прямой:

Асимптотические направление: Направление, определяемое вектором, компоненты которого удовлетворяют уравнению Aα2+2Bαβ+Cβ2 называется асимптотическим направлением линии второго порядка.
Классификация уравнений второго порядка по их числу:
17. Поверхности второго порядка. Поверхности вращения. Общее уравнение поверхности вращения. Эллипсоид вращения. Эллипсоид.
Поверхности второго порядка: ы
Поверхности вращения: Поверхность S называется поверхностью вращения с осью d, если она составлена из окружностей, которые имеют центра на прямой d и лежат в плоскостях, перпендикулярных этой прямой.
 Общее
уравнение поверхности вращения :
Общее
уравнение поверхности вращения :
![]()
Эллипсоид вращения: Направив вектор e1 сначала вдоль малой оси эллипса, а затем вдоль большой, мы получим уравнение эллипса в следующих видах:
![]()
 Эллипсоид:
Поверхность,
которая в некоторой декартовой
прямоугольной системе координат имеет
уравнение
Эллипсоид:
Поверхность,
которая в некоторой декартовой
прямоугольной системе координат имеет
уравнение
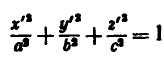 ,
назовем эллипсоидом. Причем если b=c,
то мы получим эллипсоид вращения.
,
назовем эллипсоидом. Причем если b=c,
то мы получим эллипсоид вращения.
18. Конус второго порядка. Параболоид. Однополостной и двуполостной гиперболоиды. Гиперболический параболоид
. К онус
второго порядка: Поверхность
на рисунке , получаемая вращением линии
a2x2-c2z2=0
вокруг оси аппликат, имеет уравнение
a3(x2+y2)-c2z3=0
и носит название прямого кругового
конуса. Сжатие к плоскости Y
переводит прямой конус в поверхность
с уравнением a2x2+b2y2-c2z2=0.
Поверхность, которая в некоторой
декартовой прямоугольной системе
координат имеет это уравнение, называется
конусом второго порядка.
онус
второго порядка: Поверхность
на рисунке , получаемая вращением линии
a2x2-c2z2=0
вокруг оси аппликат, имеет уравнение
a3(x2+y2)-c2z3=0
и носит название прямого кругового
конуса. Сжатие к плоскости Y
переводит прямой конус в поверхность
с уравнением a2x2+b2y2-c2z2=0.
Поверхность, которая в некоторой
декартовой прямоугольной системе
координат имеет это уравнение, называется
конусом второго порядка.
Параболо́ид ― тип поверхности второго порядка. Параболоид может быть охарактеризован как незамкнутая нецентральная (т.е. не имеющая центра симметрии) поверхность второго порядка.
Канонические уравнения параболоида в декартовых координатах:
z = ax2 + by2,
если a и b одного знака, то параболоид называется эллиптическим.
если a и b разного знака, то параболоид называется гиперболическим.
если одно a либо b равно нулю, то параболоид называется параболическим цилиндром.
Однополостной
и двуполостной гиперболоиды: Поверхность,
которая в некоторой декартовой
прямоугольной системе координат имеет
уравнение
![]() называется однополосным гиперболоидом.
называется однополосным гиперболоидом.
Поверхность,
которая в некоторой декартовой
прямоугольной системе координат имеет
уравнение
![]() называется двуполосным гиперболоидом
называется двуполосным гиперболоидом

Гиперболический
параболоид: Поверхность,
которая в некоторой декартовой
прямоугольной системе координат имеет
уравнение
![]() называется гиперболическим параболоидом.
называется гиперболическим параболоидом.
