12. Уравнения линий и поверхностей. Полярная система координат. Прямая линия на плоскости. Различные виды уравнений. Взаимное расположение прямых.

Уравнения линий и поверхностей: Это такое равенство, которое можно рассматривать как запись определения линии или поверхности при помощи координат в рассматриваемой системе, например y=f(x)

Полярная система координат: Полярная система координат употребляется на плоскости и она определена, если задана точка О, называемая полюсом и исходящий из нее луч l, который мы назовем полярной осью. Положение точки фиксируется двумя числами: Радиусом r и углом φ между полярной осью и r.

Прямая линия на плоскости: Положение прямой на плоскости определяется параметрическими уравнениями линии на плоскости х=f(t) y=g(t) (1). Где t – параметр, имеющий физический смысл времени, что, однако, не является существенным. Уравнение линии есть лишь высказывание о координатах точек. То есть формулировка такова: существует такое число t , что выполняются равенства (1).

Различные виды уравнений для прямой: 1)Направленный вектор 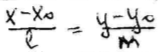2)Две точки 3)Прямая y=kx+b 4) L₁=A₁x+B₁y+С₁=0

Взаимное расположение прямых: Две прямые задаются уравнениями: L₁=A₁x+B₁y+С₁=0 и L₂=A₂x+B₂y+С₂=0. Две прямые совпадают, когда A₁\ A₂= B₁\ B₂= С₁\ С₂, параллельны когда A₁\ A₂= B₁\ B₂ и не равно С₁\ С₂, перпендикулярны cosα=0 и A₁ A₂+ B₁ B₂=0. Две прямые называются скрещивающимися, если они не лежат в одной плоскости.

13. Уравнения плоскостей и прямых в пространстве.

Поверхности и линии первого порядка: Ax+By+Cz+D=0 Уравнение первой степени или линейное уравнение, связывающее координаты точки в пространстве. Теорема1:В общей декартовой системе координат в пространстве каждая плоскость может быть задана линейным уравнением. Теорема2:В общей декартовой системе координат на плоскости каждая прямая линия может быть задана линейным уравнением. Векторное параметрическое уравнение: r-r₀=ta

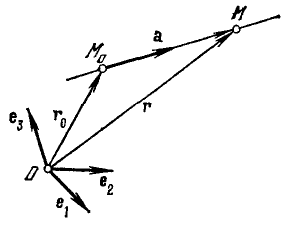
Параметрические уравнения плоскости: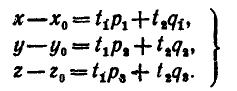

Параметрические уравнения прямой на плоскости и в пространстве:

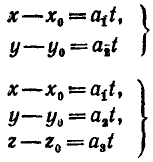
Векторное параметрическое уравнение плоскости:

Векторное уравнение плоскости:

14. Линии второго порядка. Эллипс. Гипербола. Канонические уравнение. Фокальные расстояния. Эксцентриситеты.

Линии второго порядка: Уравнение линии второго порядка Ax²+2Bxy+Cy²+2Dx+2Ey+F=0. Линия, которая в некоторой декартовой прямоугольной системе координат может быть задана уравнением называется эллипсом, а уравнение каноническим. 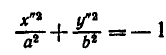- мнимый эллипс. - две мнимые пересекающиеся прямые. - гипербола и её канонической уравнение. - парабола. - пара параллельных прямых. - пара мнимых параллельных прямых.

Эллипс: Линия, которая в некоторой декартовой прямоугольной системе координат может быть задана уравнением называется эллипсом, а уравнение каноническим.

Оси координат канонической системы – оси симметрии эллипса, а центр – центр симметрии. С²=a²-b², Два фокуса F₁(c,0) и F₂(-c,o). Экцентриситет e=c\a. Расстояние от произвольной точки M(x,y), лежащей на эллипсе до каждого из фокусов является линейной функцией от ее абциссы х : Для того чтобы точка лежала на эллипсе, необходимо и достаточно, чтобы сумма ее расстояний до фокусов равнялось большой оси эллипса 2а.

Гипербола: Линия, которая в некоторой декартовой прямоугольной системе координат может быть задана уравнением называется эллипсом, а уравнение каноническим.

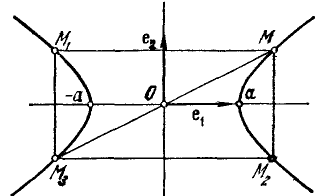Оси координат канонической системы – оси симметрии гиперболы, а центр – центр симметрии. Прямые с уравнениями y=bx\a и y=-bx\a в канонической системе координат называются асимптотами гиперболы. Экцентриситет e=c\a. C²=a²+b² Два фокуса F₁(c,0) и F₂(-c,o). Для того чтобы точка лежала на гиперболе, необходимо и достаточно, чтобы разность ее расстояний до фокусов по абсолютной величине равнялась вещественной оси гиперболы. Касательная к гиперболе есть биссектриса угла между отрезками, соединяющими эту точку с фокусами.