9. Определение вектора и операции над ними. Свойства операций над векторами. Линейная зависимость векторов. Геометрический смысл линейной зависимости. Базис.

Определение вектора и операции над ними: Направленный отрезок (или упорядоченная пара точек) мы будем называть вектором. К векторам будем относить и так называемый нулевой вектор, у которого начало и конец совпадают.

Пусть даны два вектора a и b. Построим равные им векторы AB и BC(то есть перенесем конец а и начало b в одну и ту же точку B). Тогда вектор AC называется суммой векторов а и b и обозначается a+b.

Произведением вектора а на вещественное число α называется любой вектор b, удовлетворяющий следующим условиям: 1)|b|=|α||a| 2)вектор b коллинеарен вектору а 3)векторы b и а направлены одинаково, если α>0, и противоположны, если α<0.

Свойства операций над векторами: 1)Сложение векторов коммутативно, т.е для любых векторов a и b выполнено a+b= b+а 2)Ассоциативно 3)а+0=а 4)а+(-1)а=0 5)Умножение вектора на число ассоциативно 6)Умножение вектора на число дистрибутивно по отношению к сложению чисел 7) Умножение вектора на число дистрибутивно по отношению к сложению векторов 8)1а=а

Линейная зависимость векторов: Векторы a₁…a_n называются линейно зависимыми, если существует нетривиальная линейная комбинация этих векторов, равная нулю

Геометрический смысл линейной зависимости: Любые два коллинеарных вектора линейно зависимы, и наоборот, два линейно зависимых вектора коллинеарны. Любые три компланарных вектора линейно зависимы, и наоборот, три линейно зависимых вектора – компланарны. Каждые четыре вектора линейно зависимы

Базис: Базисом в пространстве называют три некомплиарных вектора, взятые в определенном порядке. Базисом на плоскости называются два неколлинеарных вектора на этой плоскости, взятые в определенном порядке. Базисом на прямой называется любой нулевой вектор на этой прямой.

10. Скалярное произведение векторов. Свойства скалярного произведения векторов. Длины векторов и углы между ними. Скалярное произведение векторов в координатной форме. Матрица Грама.

Скалярное произведение векторов: Скалярным произведением двух векторов называется число, равное произведению длин этих векторов на косинус угла между ними. Если хоть один из векторов нулевой , то угол не определен, и скалярное произведение по определению считают равным нулю. (a,b)=|a||b|cosγ

Свойства скалярного произведения векторов: 1)Скалярное произведение коммутативно, т.е. для любых векторов a и b справедливо равенство (а,b)=(b,a) 2)(a,a)=|a|² для любого вектора а 3)Скалярное произведение равно нулю тогда и только тогда, когда сомножители ортогональны или хотя бы один из них равен нулю 4)Векторы ортогонального базиса удовлетворяют соотношениям:

Длины векторов и углы между ними: Назовем длиной вектора х и обозначим |x| число корень из (х,х). Углом между векторами х и у назовем каждое число φ, удовлетворяющее условию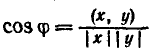

Скалярное произведение векторов в координатной форме:

Матрица Грамма:

Эта матрица называется матрицей Грамма базиса e₁…e_n. Данная матрица не меняется при транспонировании, т.е. она симметричная

11. Векторное произведение двух векторов. Свойства векторного произведения. Векторное произведение двух векторов в координатной форме. Смешанное произведение трех векторов. Свойства смешанного произведения трех векторов.

Векторное произведение двух векторов: Пусть даны векторы a и b, построим вектор с, удовлетворяющий условиям: 1) |c|=|a||b|sinφ где φ – угол между а и b 2) Вектор ортогонален векторам a и b 3)Если a и b не коллинеарны, то векторы a,b,c образуют правую тройку векторов. Вектор с будет векторным произведением a и b и обозначаться [a,b].

Свойства векторного произведения: Для любых векторов a,b,c и любых чисел λ и μ имеет место равенство:

Векторное произведение двух векторов в координатной форме:

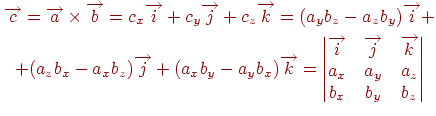
Смешанное произведение трех векторов: Число(а[b,c]) называется смешанным произведением векторов a,b,c и обозначается (a,b,c).

Свойства смешанного произведения трех векторов: Смешанное произведение некомпланарных векторов a,b,c по модулю равно объёму параллелепипеда, построенного на сомножителях. Оно положительно, если тройка a,b,c правая и отрицательно если левая. Смешанное произведение равно нулю тогда и только тогда, когда сомножители компланарны.