27 Динамические характеристики. Запаздывающее звено.

В соответствии с формулой передаточной функции звена частотные характеристики запаздывающего звена:

Т.к. АЧХ =1 и не зависит от частоты, а ФЧХ= частоте с коэффициентом пропорциональности = , то АФХ- окружность единичного радиуса с центром в начале координат.

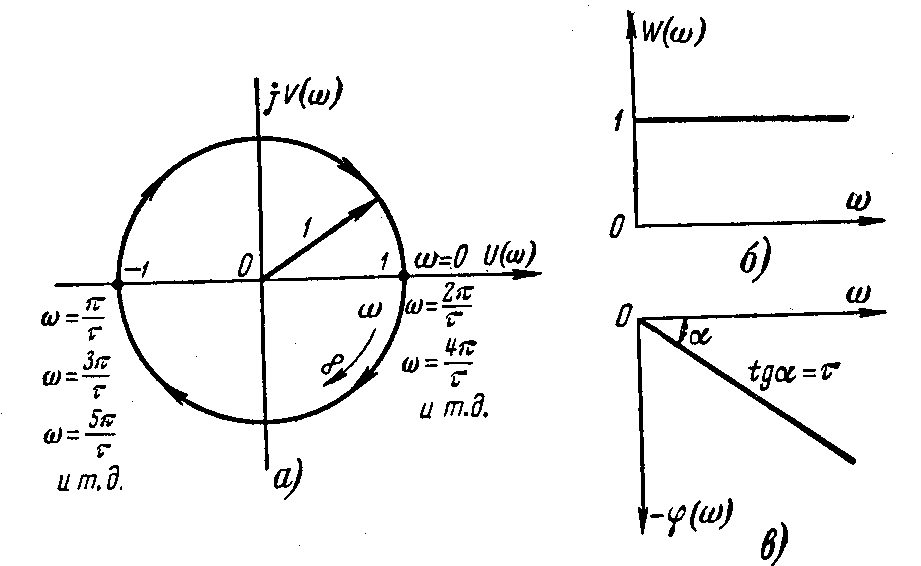
При вектор АФХ совпадает с + вещественной полуосью, и конец вектора расположен в точке (1,j0). При увеличении частоты конец вектора АФХ поворачивается по окружности в направлении часовой стрелки, т.к. ФЧХ -. При бесконечном увеличении частоты вектор бесчисленное число раз поворачивается вокруг начала координат. При его повороте на он занимает первоначальное положение.

Так как приращение фазы при этом= , то . =>в исходное положение вектор АФХ вернется при частоте . При дальнейшем увеличении частоты вектор будет занимать исходное положение при частотах и т.д. Соответственно «-» вещественная полуось будет совпадать с вектором при частотах и т.д. И при этом конец вектора будет находится в точке (-1, j0). Запаздывающее звено на выходе воспроизводит входные колебания без искажения по форме, но с отставанием по фазе.

Логарифмическая АЧХ звена - прямая, совпадающая с осью абсцисс. Логарифмическая ФЧХ строится по выражению в полулогарифмическом масштабе.

28 Устойчивость линейных систем автоматического регулирования

Понятие устойчивости, сформулированное для объектов управления и для отдельных звеньев, распространяется и на САР. Устойчивость-способность САР возвращаться к исходному состоянию после кратковременного внешнего воздействия. САР должны быть устойчивыми. Необходимое(достаточное) условие устойчивости линейной САР-отрицательность вещественных частей всех корней ее характ.ур-ия. Получим это из передаточной функции замкнутой системы, связывающей любые ее вход и выход, путем приравнивания нулю знаменателя передаточной функции (а, в – замкнутые системы; б – разомкнутая система)

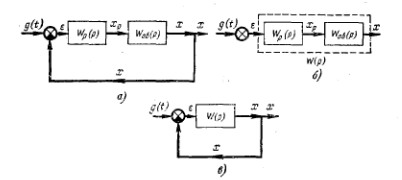
Это структурная схема, к которой может быть приведена любая односвязная линейная САР при отсутствии всех внешних воздействий кроме задающего. Передаточная функция разомкнутой системы ,где K(p) и D(p) – полиномы степеней m и n , то передаточная функция замкнутой системы

, откуда приравнивания знаменатель к 0 получим характ. ур-ие замкнутой системы степени: .

Обозначая, запишем характ. ур-ие в виде .

29 Критерий устойчивости Найквиста

Знаменатель передаточной функции замкнутой системы автоматического регулирования представляет собой функцию , на единицу отличающуюся от передаточной функции разомкнутой системы . С учетом выражения получим:

Т.к. в реальных системах порядок оператора правой части ДУ всегда меньше порядка оператора левой части, т.е. степень многочлена всегда больше степени многочлена , то степени числителя и знаменателя одинаковы и определяются степенью , равной .

Проводим подстановку, получим передаточную функцию замкнутой системы

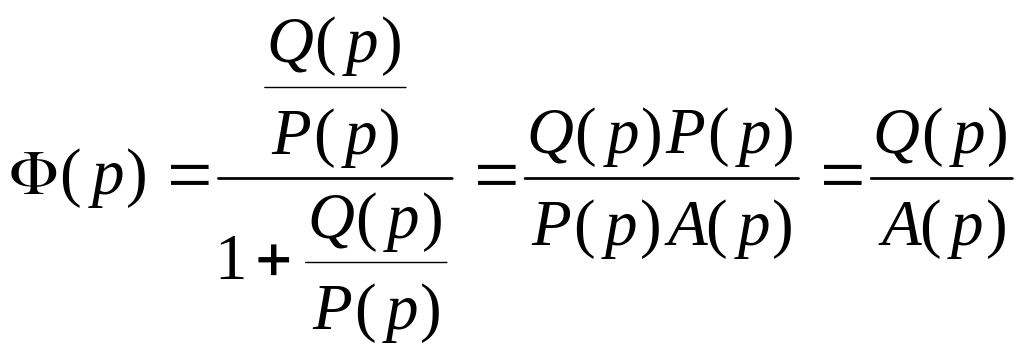. Многочлен знаменателя передаточной функции есть характ.многочлен ДУ замкнутой системы, составляющий левую часть характ. Ур-ия , корни которого позволяют найти общее решение однородного ДУ системы. Числитель функции является характ. многочленом передаточной функции замкнутой системы, а знаменатель характ. многочленом разомкнутой системы.

Перейдем от оператора в формуле получим функцию , на единицу отличающуюся от АФХ разомкнутой системы . Тогда частотная функция запишется так: , где - годограф Михайлова замкнутой системы; - годограф Михайлова разомкнутой системы. В показательной форме можно записать:

где .При изменении от 0 до полное приращение фазы функции будет равно: .

Для работоспособности системы необходимо, чтобы в рабочем (замкнутом) состоянии она была устойчивой. Это требование, согласно критерию устойчивости Михайлова выражается условием .В разомкнутом состоянии в общем случае система может быть и неустойчивой, однако если в замкнутом рабочем состоянии она устойчива, то этого достаточно для ее нормальной работы.

Принимая в общем случае, что в разомкнутом состоянии система неустойчива и ее характ.у-ие имеет корней справа от мнимой оси, согласно формуле ( ) критерия Михайлова запишем: .Таким образом, .Т.к. выражение обеспечивает отсутствие корней характ.ур-ия замкнутой системы справа от мнимой оси, то оно является необходимым и достаточным условием устойчивости системы и называется критерием устойчивости Найквиста. Если , то замкнутая система неустойчива. Критерий устойчивости Найквиста можно сформулировать следующим образом:

Замкнутая линейная система устойчива, если приращение фазы функции при изменении от 0 до будет равно , где - число корней характеристического уравнения разомкнутой системы, лежащих на комплексной плоскости справа от мнимой оси.

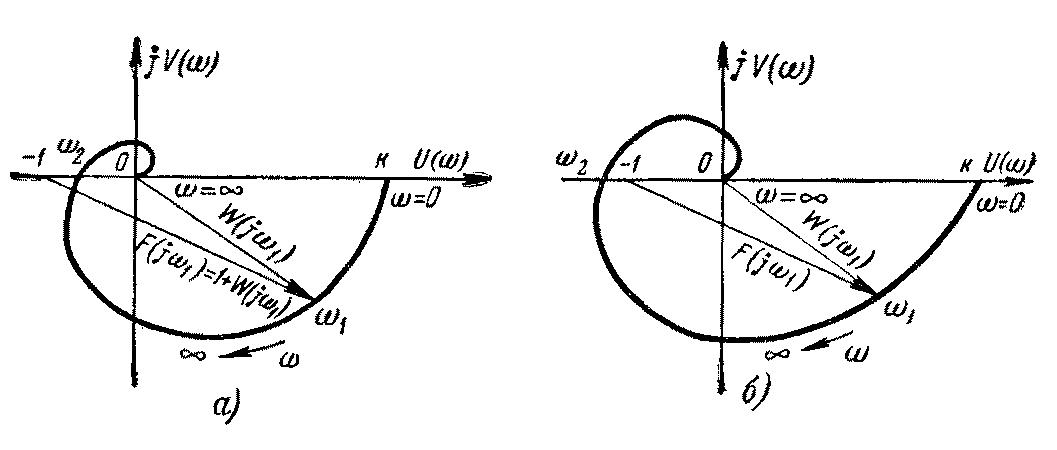
Рис.5.5. Амплитудно-фазовые характеристики а – устойчивые в замкнутом состоянии; б – неустойчивые в замкнутом состоянии.