25 Динамические характеристики. Интегро-дифференцирующее звено.

В соответствии с передаточной ф-ей звена АФХ: . Вещественная и мнимая частотные характеристики: .

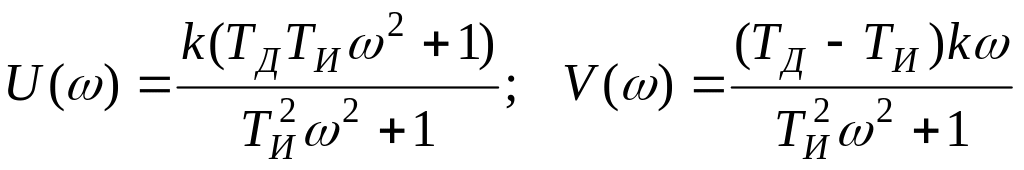АЧХ и ФЧХ звена: . .

АФХ можно представить в виде явной функции .

Без вывода АФХ : .

где .АФХ имеет вид окружности, центр которой расположен на вещественной положительной полуоси в точке с координатами ( ). Радиус окружности равен . АФХ для двух различных соотношений постоянных времени и на 1 рис. АЧХ и ФЧХ на 2 рис.

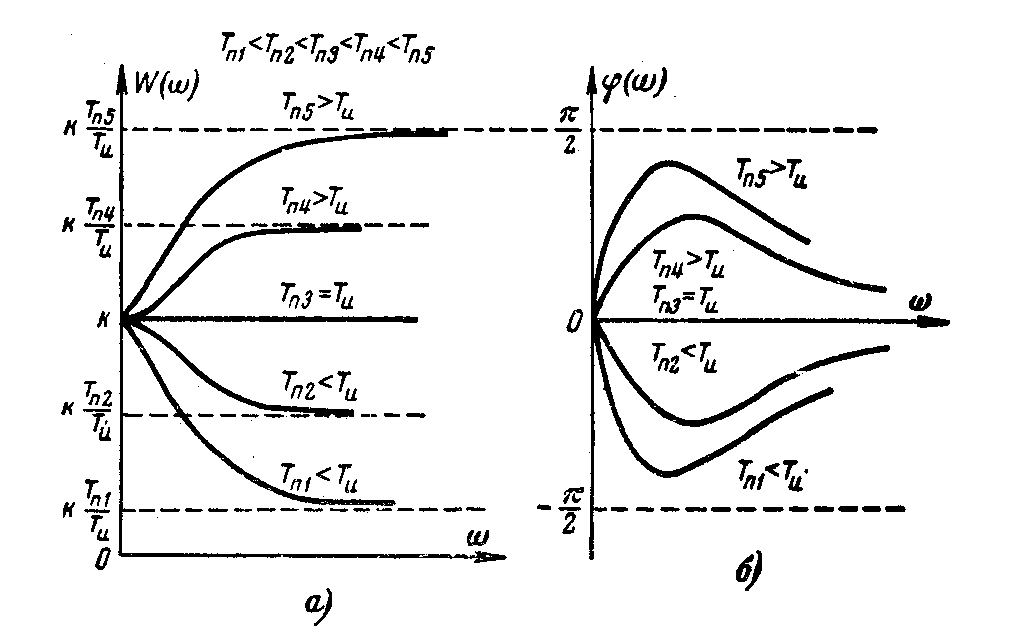
На малых частотах входных колебаний звено ведет как усилительное с коэффициентом усиления . Колебания проходят через звено без искажений по фазе, т.к . На больших частотах входных колебаний ( ) звено также ведет себя как усилительное, но с коэффициентом усиления, равным . При этом ФЧХ стремится к нулю. На средних частотах выходные колебания или опережают входные колебания ( ), или отстают от них ( ).

При интегро-дифференцирующее звено по своим свойствам приближается к дифференцирующему звену.

При интегро-дифференцирующее звено по своим свойствам приближается или к интегрирующему, или к апериодическому.

При , а , , на при этом отношение является конечной постоянной величиной, то звено превращается в интегрирующее.

Если при величины конечны, получаем апериодическое звено.

При интегро-дифференцирующее звено превращается в усилительное с коэффициентом усиления . При этом на всех частотах сигнал проходит через звено без фазовых искажений. Это можно объяснить: дифференцирующая составляющая дает опережение выходной величины по отношению к входной. Интегрирующая же составляющая создает отставание выходной величины от входной. При равенстве этих составляющих они взаимно уравновешивают друг друга, и результирующее воздействие их на фазу выходного сигнала равно нулю.

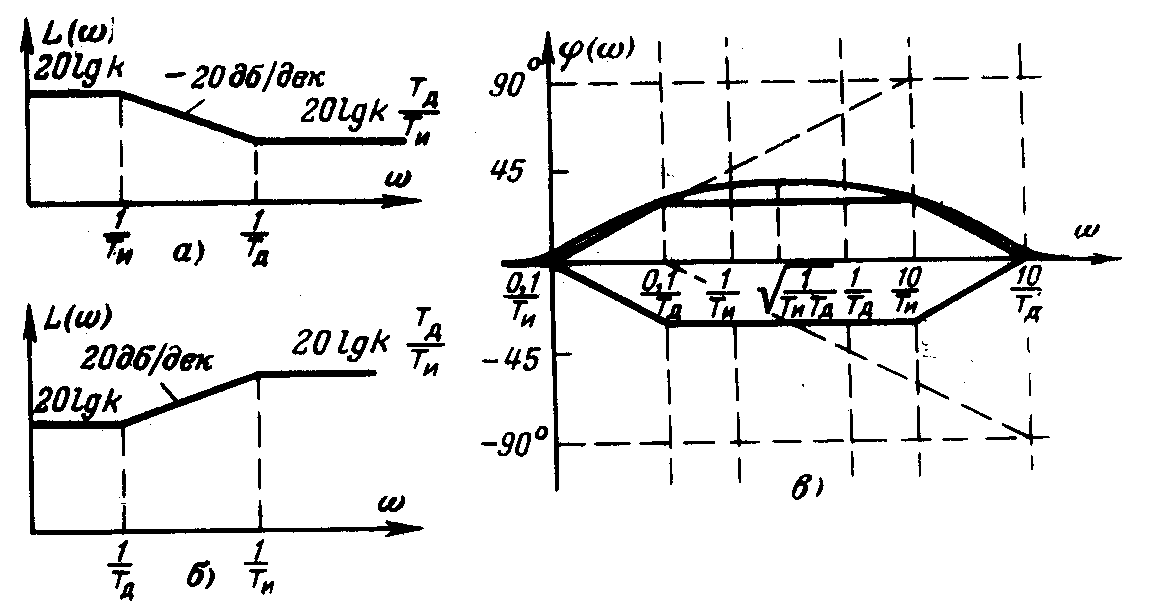
Логарифмируя выражение , получим логарифмическую АЧХ звена:

=> вид аппроксимированной ЛАЧХ звена зависит от соотношения постоянных времени и .

При в интервале между сопрягающими частотами и асимптота определяется отрезком прямой с наклоном -20 дБ/дек. При сопрягающие частоты и , а асимптота в этом диапазоне частот определяется отрезком прямой с наклоном +20 дБ/дек.В интервале низких частот ЛАЧХ аппроксимируется прямой , а в интервале высоких частот - прямой .

При последовательном соединении двух интегро-дифференцирующих звеньев получаем также интегро-дифференцирующее звено. АЧХ звена:

.

Логарифмическая АЧХ :

ФЧХ звена:

26 Динамические характеристики. Инерционное звено 2 порядка

В соответствии с передаточной функцией инерционного звена второго порядка

АФХ:

Вещественная частотная характеристика

Мнимая частотная характеристика

АЧХ:

ФЧХ: АФХ звена на рисунке при разных Т1/Т2.

АФХ начинается на действительной оси в точке с абсциссой, равной . Чем больше , тем меньше колебательность звена. При колебательное звено превращается в соединение из двух апериодических звеньев 1 порядка.

При и отношение , а инерционное звено 2 порядка превращается в инерционное звено 1 порядка с постоянной времени . Тогда АФХ:

имеет вид окружности с радиусом , центр которой расположен на вещественной оси в точке ( ).

При инерционное звено 2 порядка превращается в колебательное звено. При этом, чем меньше , тем меньше отношение и тем меньше степень затухания колебаний в звене. При степень затухания будет равна 0 и возникшие колебания будут незатухающими с собственной частотой колебаний, равной .Тогда АФХ : .

Графически эта характеристика при входной величине имеет вид двух полупрямых. Первая полупрямая начинается при на вещественной положительной полуоси в точке и при возрастании уходит в бесконечность по вещественной полуоси в + направлении. Вторая полупрямая совпадает с - вещественной полуосью. Начало прямой в бесконечности при , а конец – в начале координат при , т.е. функция не определена и терпит разрыв на частоте . Такой разрыв графически представляют окружностью бесконечного радиуса.

Определяя первую производную АФХ по частоте и приравнивая полученное выражение нулю, находим:

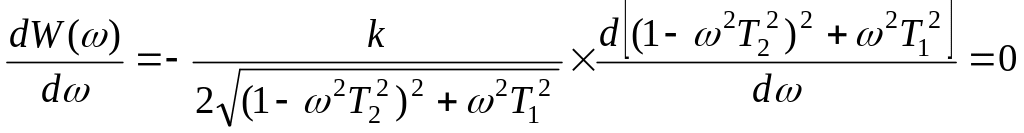
Отсюда вытекает, что

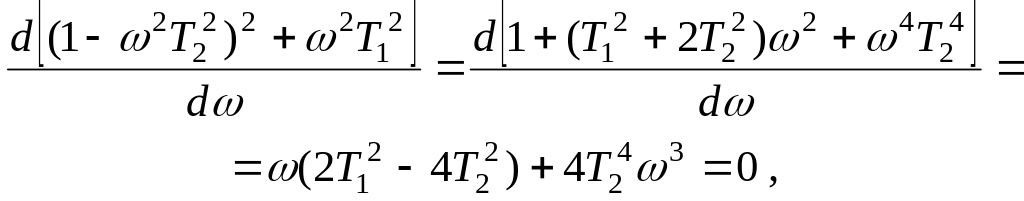
или

Из этого уравнения находим значение частот, при которых АЧХ имеет экстремумы:

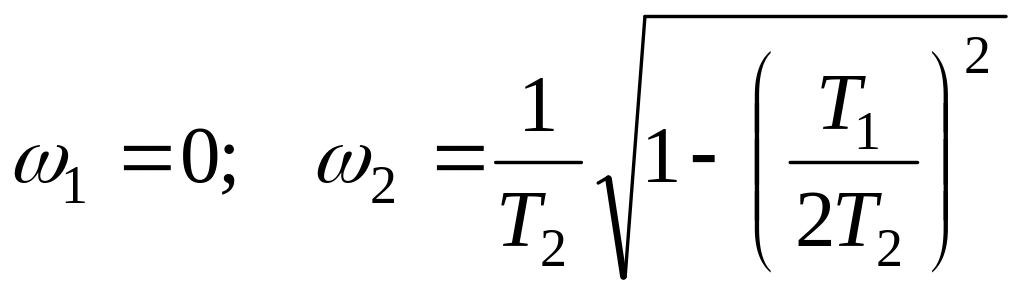
Из выражения для АЧХ следует, что при АЧХ = коэффициенту усиления инерционного звена 2 порядка: , и не зависит от величины постоянных времени , и их соотношения.

Второе вещественное экстремальное значение имеется только при . При этом, чем больше отношение приближается к значению , тем ближе подходит вторая точка экстремума к первой. На рис АФХ и ФЧХ

Рассмотрим второй экстремум кривой , появляющийся при . Из рисунка - при возрастании от до АЧХ также возрастает, начиная со значения , и при достигает max значения: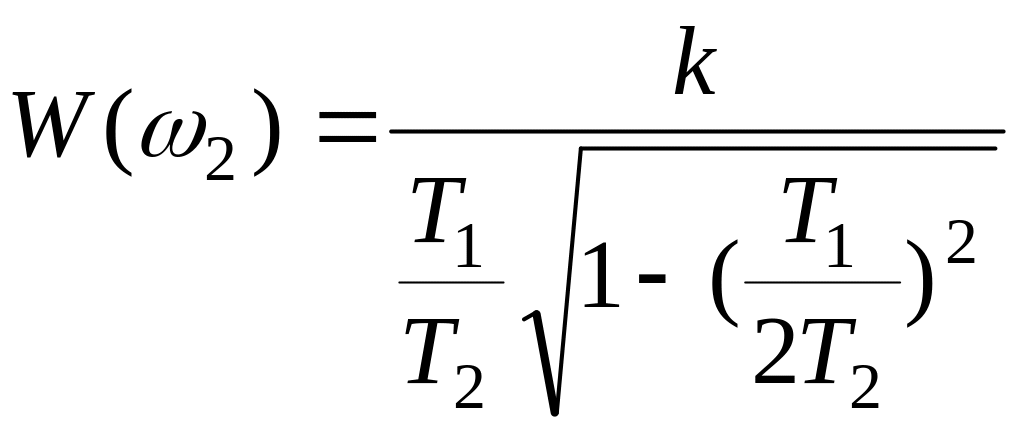 , при дальнейшем увеличении частоты АЧХ стремится к 0.

Если продолжить дальнейшее уменьшение отношения , максимум АЧХ увеличивается и приближается к собственной частоте колебаний звена .

При максимум . АЧХ при этом совпадает с АФХ. Если входная величина является постоянной ( ), то . Если частота входной величины стремится к бесконечности, то АЧХ стремится к 0.

Всё семейство характеристик для различных отношений равно нулю при , равно при частоте и стремится к при частоте . Так как -, то выходные колебания во всем диапазоне изменения отстают от входных колебаний.

При фаза выходных колебаний совпадает с фазой входных колебаний в диапазоне изменений от . При происходит изменение фазы скачком от до , и в диапазоне изменения от фаза выходных колебаний отстает от фазы входных колебаний на .

Построение асимптотических ЛЧХ. АФХ можно записать:

Проводим вспомогательные вертикальные линии через сопрягающие частоты и . Для определенности построения принято, что .

ЛАХ строится по выражению . (*)

Построение ЛЧХ изображено на рис.

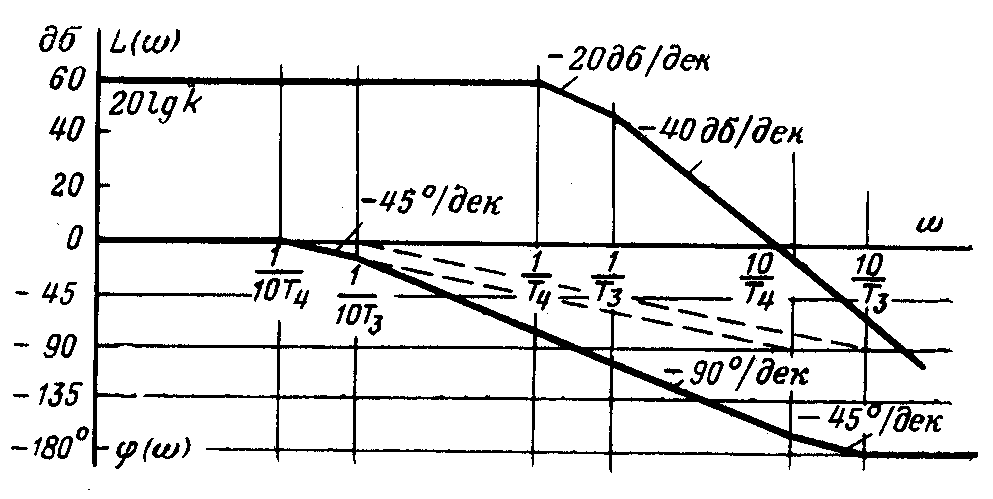
Левее первой сопрягающей частоты ( ), это выражение заменяется приближенным ,которому соответствует горизонтальная прямая (1 асимптота ЛАХ).

Для частот выражение(*) заменяется ,кот. соответствует прямая с - наклоном -20 дБ/дек (2 асимптота).

Для частот выражение (*) заменяется , которому соответствует прямая с - наклоном -40 дБ/дек. (3 асимптота). Действительная ЛАХ - пунктир. Она отличается от асимптотической в точках излома на 3 дБ.

ФЧХ: .

При построении логарифмической ФЧХ типа , знаменатель м.б 0 или -. Во избежание ошибки (при ) вычисления фазового сдвига тригонометрических функций необходима ручная коррекция главного значения .