
3)Структуры данных. Очередь, стек.
Структура данных — программная единица, позволяющая хранить и обрабатывать множество однотипных и/или логически связанных данных
Очередь — структура данных с дисциплиной доступа к элементам «первый пришёл — первый вышел». Добавление элемента возможно лишь в конец очереди, выборка — только из начала очереди, при этом выбранный элемент из очереди удаляется.

Обычно start указывает на голову очереди, end — на элемент, который заполнится, когда в очередь войдёт новый элемент. При добавлении элемента в очередь в q[end] записывается новый элемент очереди, а end уменьшается на единицу. Если значение end становится меньше 1, то мы как бы циклически обходим массив и значение переменной становится равным n. Извлечение элемента из очереди производится аналогично: после извлечения элемента q[start] из очереди переменная start уменьшается на 1. С такими алгоритмами одна ячейка из n всегда будет незанятой (так как очередь с n элементами невозможно отличить от пустой), что компенсируется простотой алгоритмов.
Преимущества данного метода: возможна незначительная экономия памяти по сравнению со вторым способом; проще в разработке.
Недостатки: максимальное количество элементов в очереди ограничено размером массива. При его переполнении требуется перевыделение памяти и копирование всех элементов в новый массив.
Стек— структура данных, в которой доступ к элементам организован по принципу LIFO (англ. last in — first out, «последним пришёл — первым вышел»). Чаще всего принцип работы стека сравнивают со стопкой тарелок: чтобы взять вторую сверху, нужно снять верхнюю.

Добавление элемента, называемое также проталкиванием (push), возможно только в вершину стека (добавленный элемент становится первым сверху). Удаление элемента, называемое также выталкиванием (pop), тоже возможно только из вершины стека, при этом второй сверху элемент становится верхним.
4) Структуры данных. Односвязный, двухсвязный список. Линейные и кольцевые списки.
Структура данных — программная единица, позволяющая хранить и обрабатывать множество однотипных и/или логически связанных данных
В информатике, список — это абстрактный тип данных, представляющий собой упорядоченный набор значений, в котором некоторое значение может встречаться более одного раза.
Односвязный список (Однонаправленный связный список)

Здесь ссылка в каждом узле указывает на следующий узел в списке. В односвязном списке можно передвигаться только в сторону конца списка. Узнать адрес предыдущего элемента, опираясь на содержимое текущего узла невозможно.
Двусвязный список (Двунаправленный связный список)
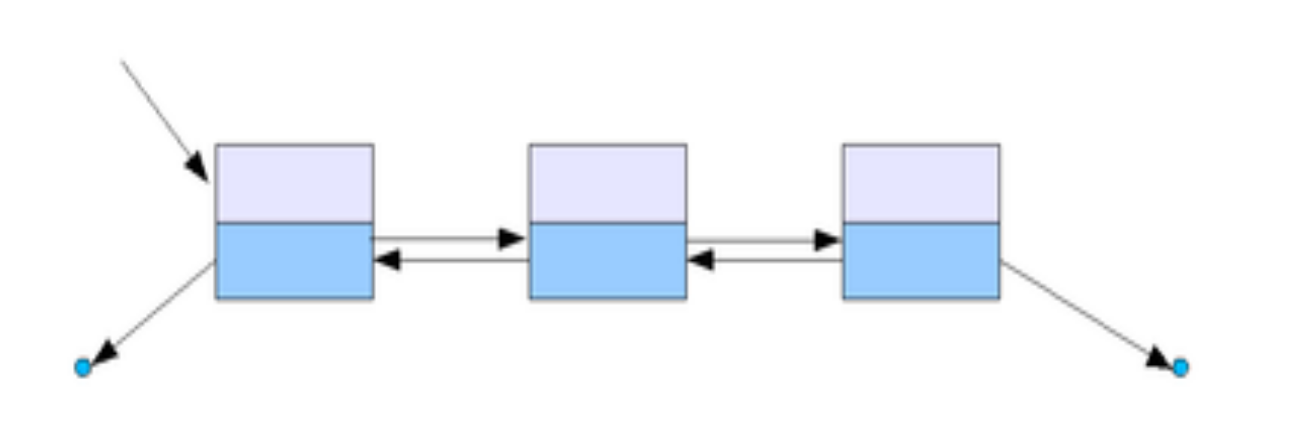
Здесь ссылки в каждом узле указывают на предыдущий и на последующий узел в списке. По двусвязному списку можно передвигаться в любом направлении — как к началу, так и к концу. В этом списке проще производить удаление и перестановку элементов, так как всегда известны адреса тех элементов списка, указатели которых направлены на изменяемый элемент.
Линейный однонаправленный список — это структура данных, состоящая из элементов одного типа, связанных между собой.
В информатике линейный список обычно определяется как абстрактный тип данных (АТД), формализующий понятие упорядоченной коллекции данных.
На практике линейные списки обычно реализуются при помощи массивов и связных списков. Иногда термин «список» неформально используется также как синоним понятия «связный список».
К примеру, АТД нетипизированного изменяемого списка может быть определён как набор из конструктора и четырёх основных операций:
операция, проверяющая список на пустоту;
операция добавления объекта в список;
операция определения первого (головного) элемента списка;
операция доступа к списку, состоящему из всех элементов исходного списка, кроме первого.
Кольцевой связный список
Разновидностью связных списков является кольцевой (циклический, замкнутый) список. Он тоже может быть односвязным или двусвязным. Последний элемент кольцевого списка содержит указатель на первый, а первый (в случае двусвязного списка) — на последний.
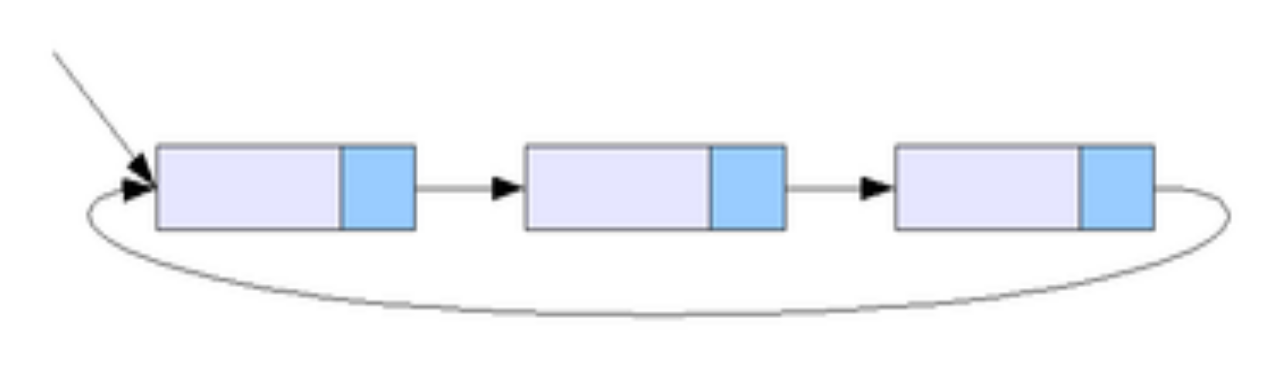
Реализация такой структуры происходит на базе линейного списка. С каждым кольцевым списком есть указатель на первый элемент. В этом списке константы NULL не существует.
Так же существуют циклические списки с выделенным головным элементом, облегчающие полный проход через список.
5) Задачи сортировки. Свойства алгоритмов сортировки. Сортировка пузырьком. Модификации.
Задачи сортировки:
Задача сортировки заключается в том, чтобы каждый элемент некоторой последовательности удовлетворял условию, что каждый последующий элемент больше предыдущего.
Свойства алгоритмов сортировки:
1 время сортировки – основной параметр, характеризующий быстродейственность алгоритма.
2 память – ряд алгоритмов требует выделения дополнительной памяти под временное хранение данных. При оценке используемой памяти обычно не учитывается место, которое занимает исходный массив и не зависящие от входной последовательности затраты памяти, например, на хранение кода программы.
3 устойчивость. Устойчивая сортировка не меняет взаимного расположения элементов, такое свойство может быть очень полезным, если элементы состоят из нескольких полей, причем сортировка происходит по одному из них.
4 естественность поведения – эффективность метода при обработке уже отсортированных или частично отсортированных данных. Алгоритм будет вести себя естественно, если учитывает эту характеристику входной последовательности и ведет себя лучше.
5 сфера применения. Внутренние сортировки – они работают с данными в оперативной памяти с произвольным доступом. Внешние сортировки – упорядочивают информацию, расположенную на внешних носителях, есть некоторые ограничения: доступ к носителю осуществляется последовательно, объем данных не позволяет разместиться в ОЗУ.
Сортировка пузырьком.
Идея: шаг сортировки состоит в проходе снизу вверх по массиву, по пути просматриваются пары соседних элементов. Если элементы некоторой пары находятся в неправильном порядке, то их меняют местами.
Методы улучшения: первое улучшение заключается, в запоминании производился ли на данном проходе какой-либо обмен. Если нет, алгоритм заканчивает работу; процесс улучшения можно продолжить, если запоминать не только сам факт обмена, но и индекс последнего обмена.
6) Задачи сортировки. Свойства алгоритмов сортировки. Сортировка вставками. Модификации.
Сортировка вставками.
Идея: делаются проходы по части массива, и в его начале "вырастает" отсортированная последовательность. Последовательность a[0]...a[i] упорядочена. При этом по ходу алгоритма в нее будут вставляться (см. название метода) все новые элементы. Как говорилось выше, последовательность к этому моменту разделена на две части: готовую a[0]...a[i] и неупорядоченную a[i+1]...a[n]. На следующем, (i+1)-м каждом шаге алгоритма берем a[i+1] и вставляем на нужное место в готовую часть массива. Поиск подходящего места для очередного элемента входной последовательности осуществляется путем последовательных сравнений с элементом, стоящим перед ним. В зависимости от результата сравнения элемент либо остается на текущем месте (вставка завершена), либо они меняются местами и процесс повторяется.
Модификация.
Алгоритм можно слегка улучшить. Заметим, что на каждом шаге внутреннего цикла проверяются 2 условия. Можно объединить из в одно, поставив в начало массива специальный сторожевой элемент. Он должен быть заведомо меньше всех остальных элементов массива. Тогда при j=0 будет заведомо верно a[0] <= x. Цикл остановится на нулевом элементе, что и было целью условия j>=0. Таким образом, сортировка будет происходить правильным образом, а во внутреннем цикле станет на одно сравнение меньше. Однако, отсортированный массив будет не полон, так как из него исчезло первое число. Для окончания сортировки это число следует вернуть назад, а затем вставить в отсортированную последовательность a[1]...a[n].
7) Задачи сортировки. Свойства алгоритмов сортировки. Сортировка Шелла. Модификации.
Сортировка Шелла.
Сортировка Шелла является довольно интересной модификацией алгоритма сортировки простыми вставками. Рассмотрим следующий алгоритм сортировки массива a[0].. a[15].
1. Вначале сортируем простыми вставками каждые 8 групп из 2-х элементов (a[0], a[8[), (a[1], a[9]), ... , (a[7], a[15]).
2. Потом сортируем каждую из четырех групп по 4 элемента (a[0], a[4], a[8], a[12]), ..., (a[3], a[7], a[11], a[15]). В нулевой группе будут элементы 4, 12, 13, 18, в первой - 3, 5, 8, 9 и т.п.
3. Далее сортируем 2 группы по 8 элементов, начиная с (a[0], a[2], a[4], a[6], a[8], a[10], a[12], a[14]).
4. В конце сортируем вставками все 16 элементов. Очевидно, лишь последняя сортировка необходима, чтобы расположить все элементы по своим местам. Hа самом деле они продвигают элементы максимально близко к соответствующим позициям, так что в последней стадии число перемещений будет весьма невелико. Последовательность и так почти отсортирована. Ускорение подтверждено многочисленными исследованиями и на практике оказывается довольно существенным. Единственной характеристикой сортировки Шелла является приращение - расстояние между сортируемыми элементами, в зависимости от прохода. В конце приращение всегда равно единице - метод завершается обычной сортировкой вставками, но именно последовательность приращений определяет рост эффективности.
Модификация.
Использованный в примере набор ..., 8, 4, 2, 1 - неплохой выбор,
особенно, когда количество элементов - степень двойки. Однако гораздо
лучший вариант предложил Р.Седжвик. Его последовательность имеет вид

При использовании таких приращений среднее количество операций: O(n7/6), в худшем случае - порядка O(n4/3). Обратим внимание на то, что последовательность вычисляется в порядке, противоположном используемому: inc[0] = 1, inc[1] = 5, ... Формула дает сначала меньшие числа, затем все большие и большие, в то время как расстояние между сортируемыми элементами, наоборот, должно уменьшаться. Поэтому массив приращений inc вычисляется перед запуском собственно сортировки до максимального расстояния между элементами, которое будет первым шагом в сортировке Шелла. Потом его значения используются в обратном порядке. При использовании формулы Седжвика следует остановиться на значении
inc[s-1], если 3*inc[s] > size.
int increment(long inc[], long size) {
int p1, p2, p3, s;
p1 = p2 = p3 = 1;
s = -1;
do {
if (++s % 2) {
inc[s] = 8*p1 - 6*p2 + 1;
} else {
inc[s] = 9*p1 - 9*p3 + 1;
p2 *= 2;
p3 *= 2;
}
p1 *= 2;
} while(3*inc[s] < size);
return s > 0 ? --s : 0;
}
void shellSort(int a[], long size) {
long inc, i, j, seq[40];
int s;
// вычисление последовательности приращений
s = increment(seq, size);
while (s >= 0) {
// сортировка вставками с инкрементами inc[]
inc = seq[s--];
for (i = inc; i < size; i++) {
int temp = a[i];
for (j = i-inc; (j >= 0) && (a[j] > temp); j -= inc)
a[j+inc] = a[j]; a[j+inc] = temp;
}
}
}
Часто вместо вычисления последовательности во время каждого запуска процедуры, ее значения рассчитывают заранее и записывают в таблицу, которой пользуются, выбирая начальное приращение по тому же правилу: начинаем с inc[s-1], если 3*inc[s] > size
8) Задачи сортировки. Свойства алгоритмов сортировки. Пирамида.
Пирамида.
Построим сортировку данных, которая позволит выбирать максимальный элемент не за О(n) времени, а за О(log(n)) , тогда общее быстродействие сортировки будет nO(log(n))=O(nlog(n)). Эта сортировка должна позволять быстро вставлять новые элементы и удалять максимальный элемент (он будет перемещаться в уже отсортированную часть массива) .
Назовем пирамидой бинарное дерево высотой К.
1 все узлы имеют глубину К ил К-1.
2 уровень К-1полность заполнен, а уровень К – заполнен слева на право.
3 каждый элемент должен быть меньше или равен родителю.
Плюсы: нет дополнительных переменных (нужно лишь понимать схему); узлы хранятся от вершины и далее вниз уровень за уровнем; узлы одного уровня хранятся в массиве слева на право.
Фазы: 1 построение пирамиды; 2 сортировка.
Свойства сортировки:
1 не использует дополнительной памяти
2 метод неустойчив
3 поведение алгоритма неестественно.
10) Задачи сортировки. Свойства алгоритмов сортировки. Быстрая сортировка.
Задача сортировки заключается в том, чтобы каждый элемент некоторой последовательности удовлетворял условию, что каждый последующий элемент больше предыдущего.
Свойства алгоритмов сортировки:
1 время сортировки – основной параметр, характеризующий быстродейственность алгоритма.
2 память – ряд алгоритмов требует выделения дополнительной памяти под временное хранение данных. При оценке используемой памяти обычно не учитывается место, которое занимает исходный массив и не зависящие от входной последовательности затраты памяти, например, на хранение кода программы.
3 устойчивость. Устойчивая сортировка не меняет взаимного расположения элементов, такое свойство может быть очень полезным, если элементы состоят из нескольких полей, причем сортировка происходит по одному из них.
4 естественность поведения – эффективность метода при обработке уже отсортированных или частично отсортированных данных. Алгоритм будет вести себя естественно, если учитывает эту характеристику входной последовательности и ведет себя лучше.
5 сфера применения. Внутренние сортировки – они работают с данными в оперативной памяти с произвольным доступом. Внешние сортировки – упорядочивают информацию, расположенную на внешних носителях, есть некоторые ограничения: доступ к носителю осуществляется последовательно, объем данных не позволяет разместиться в ОЗУ.
Быстрая сортировка.
Идея:
1 из массива выбирается некоторый опорный элемент.
2 запускается процедура разделения массива, которая перемещает все элементы <= влево от него, а все элементы >= вправо от него.
Среднее число операций O(n^(7/6)), худшее O(n^(4/3))
10) Задачи поиска. Бинарный поиск.
Задачи поиска.
1 входит ли искомый объект или набор искомых объектов в множество объектов.
2 если искомые объекты входят в множество объектов, необходимо найти их положение.
Бинарный поиск.




11) Задачи поиска. Фиббоначчиев поиск.
Задачи поиска.
1 входит ли искомый объект или набор искомых объектов в множество объектов.
2 если искомые объекты входят в множество объектов, необходимо найти их положение.



12) Задачи поиска. Интерполяционный поиск.
Задачи поиска.
1 входит ли искомый объект или набор искомых объектов в множество объектов.
2 если искомые объекты входят в множество объектов, необходимо найти их положение.




13) Основные понятия теории графов. Задача поиска в ширину и в глубину.
Основные понятия.
Граф – множество вершин и множество ребер, причем для каждого ребра указывается пара вершин, которые можно соединить.
Вершины и рёбра называются элементами графов.
Свойства:
1 граф может быть ориентирован или не ориентирован. Не ориентированным графом называется графы, в которых связи между вершинами (рёбрами) не имеют направленности. Граф называется ориентированным, если рёбра имеют направленность.
2 кратность ребер (не все графы могут иметь четные ребра). Когда из 1 вершины выходит несколько ребер. Если в графе могут быть кратные ребра, он называется мультиграф.
3 свойство петли (петлёй называется соединение вершины с самой собой)
Спец. Графы:
1 пустой граф – граф, не содержащий ни одного ребра.
2 полный граф – граф, в котором каждые 2 вершины смежные, то есть соединены.
3 цепь (путь) – граф с множеством вершин.
4 цикл – цепь, к которой добавляется ребро (замкнутая).
5 взвешенность применяется очень часто для моделирования реальных ситуаций, при этом вершинам или ребрам, или и тем и другим присваиваются некоторые числа.
Что бы эти числа не означали их называют весами, а граф с заданными весами вершин или ребер называют взвешенным графом (изоморфизм).
Изоморфизм – построение графов, при этом очень часто при исследовании строения, имена вершин роли не играют. Графы называются изоморфными, если один из другого получается путем переименования вершин.
Операции с графами.
1 удаление ребра (сохраняются все вершины и все ребра кроме удаляемого).
2 добавление ребра.
3 удаление вершины (вместе с вершиной удаляются все соединенные с ней ребра). При добавлении вершины к графу добавляется новая изоморфная вершина.
4 операция стягивания ребра: вершины а и b удаляются из графа, к нему добавляется новая вершина с и соединяется ребром с каждой вершиной, с которой была смежна хотя бы одна из вершин а и b.
5 операция подразбиения ребра: из графа удаляется ребро ab , к нему добавляется новая вершина с и 2 ребра ac и bc.
D называется подграфом, если он может быть получен из него удалением некоторых вершин или ребер.
Маршрут в графе – последовательность х1, х2… для всего маршрута соединены ребром.
Путь- маршрут, в котором все ребра различны. Цикл – замкнутый путь. Дерево – один из видов графов, связный граф, не имеющий циклов.
Поиск глубину – способ обхода вершин графа, который начавшись т какой-либо вершины рекурсивно применяется ко всем вершинам, в которые можно попасть из текущей.
В результате работы алгоритма все вершины графа оказались пройденными, при условии, что граф связный.
Поиск в ширину.
При поиске в ширину вместо stack рекурсивных вызовов, хранится очередь, в которую записываются вершины в порядке удаления от начальной. Так как вершины перебираются в порядке удаления от начальной, работу алгоритма можно представить в виде набегающей волны. Отсюда второе название “метод волны”, при помощи такого алгоритма можно искать кратчайшие пути от одной вершины до другой в невзвешенном графе.
