
- •IЭтап. Произведём первичную обработку опытных данных и сделаем предположение о законе распределения случайной величины н. (в качестве случайной величины я выбрал н).
- •Все расчёты сведём в таблицу:
- •То же самое нашли с помощью Excel:
- •Записываем данные в таблицу:
- •2. Проверка правдоподобия выдвинутой гипотезы осуществляется по критериям согласия .
- •Решение в Excel:
2. Проверка правдоподобия выдвинутой гипотезы осуществляется по критериям согласия .
Проведём
детальную проверку гипотезы о распределении
случайной величины Н по закону арксинуса
с помощью критерия согласия
![]() (хи-квадрат).
(хи-квадрат).
![]() .
.
Затем по таблице квантилей распределения (приложение 2) по уровню значимости р=0,05 и по числу степеней свободы v=k-r-1
найдём
критическое значение
![]() .
В результате вычислений получаем
.
В результате вычислений получаем
![]() .
Найдём по таблице квантилей
распределения по уровню значимости
р=0,05 и по числу степеней свободы
v=k-r-1=5-2-1=2критическое
значение
.
Найдём по таблице квантилей
распределения по уровню значимости
р=0,05 и по числу степеней свободы
v=k-r-1=5-2-1=2критическое
значение
![]() .
Так как
.
Так как
![]() ,
то нет оснований для отклонения гипотезы
о законе распределения по арксинусу СВ
Н.
,
то нет оснований для отклонения гипотезы
о законе распределения по арксинусу СВ
Н.
Решение в Excel:
|
|
|
Проверка гипотезы |
|
|
Вероятности |
|
|
|
|
|
Эмпирич. |
Теорич |
|
|
|
|
0,12 |
0,14356629 |
0,096709714 |
|
Чс.ст.св.= |
2 |
0,08 |
0,16545353 |
1,103377097 |
|
(крит)^2= |
6 |
0,2 |
0,17463422 |
0,092110063 |
|
(набл)= |
0,54509 |
0,28 |
0,16920247 |
1,813816935 |
|
|
|
0,32 |
0,34714349 |
0,053059394 |
|
|
|
|
(набл)^2 |
3,159073202 |
|
|
|
3.
Проверим гипотезу распределения СВ Н
по закону арксинуса с помощью
![]() -критерия
Колмогорова. Для этого для каждого
значения
найдём модуль разности между эмпирической
и теоретической функции распределения
-критерия
Колмогорова. Для этого для каждого
значения
найдём модуль разности между эмпирической
и теоретической функции распределения
![]() и вычислим наблюдаемое значение
выборочной статистики
Колмогорова:
и вычислим наблюдаемое значение
выборочной статистики
Колмогорова:
![]() .
.
Наблюдаемое
значение статистики
Колмогорова сравнивается с критическим
значением, определяемым по уровню
значимости р=0,05 ( приложение 4).
![]() . Так как
. Так как
![]() ,
то нет оснований для отклонения гипотезы
о законе распределении
,
то нет оснований для отклонения гипотезы
о законе распределении
СВ Н по арксинусу.
4Этап. Изучим связь между случайными величинами (Н,К).
1.Найдём
числовые характеристики выборки (среднее
арифметическое
![]() ,
,![]() ;
средние квадратичные отклонения
;
средние квадратичные отклонения
![]() ,
корреляционный момент
,
корреляционный момент
![]() ,
коэффициент корреляции
,
коэффициент корреляции
![]() и проверим значимость коэффициента
корреляции.
и проверим значимость коэффициента
корреляции.
=1516;![]() =495,927;
=495,927;
![]() ;
;
![]() =22970,9;
=22970,9;
![]() ;
;
![]() ;
;![]() .
.
Решение в Excel:
M*(x)= |
216,72 |
(X) |
151,56161 |
r*= |
0,73155771 |
K*(X;Y)= |
54986,48 |
D*(X)= |
22970,9216 |
По
числу степеней свободы v=25-2=23
и при p=0,05
в таблице квантилей r-распределения
(приложение 6) находим критическое
значение коэффициента корреляции:![]() .Так как 0,732>0,4482,то связь есть.
.Так как 0,732>0,4482,то связь есть.
2.Найдём эмпирическую функцию регрессии y на x и x на y. Запишем уравнения линейной регрессии yна x:
![]() и x
на y:
и x
на y:
![]() .
.
Получаем:y-1516=2,4(x-216,72) и x-216,72=0,22(y-1516) или
y=2,4x+995,9; x=0,22y-116,8.
3.Построим корреляционное поле и графики линии регрессии.
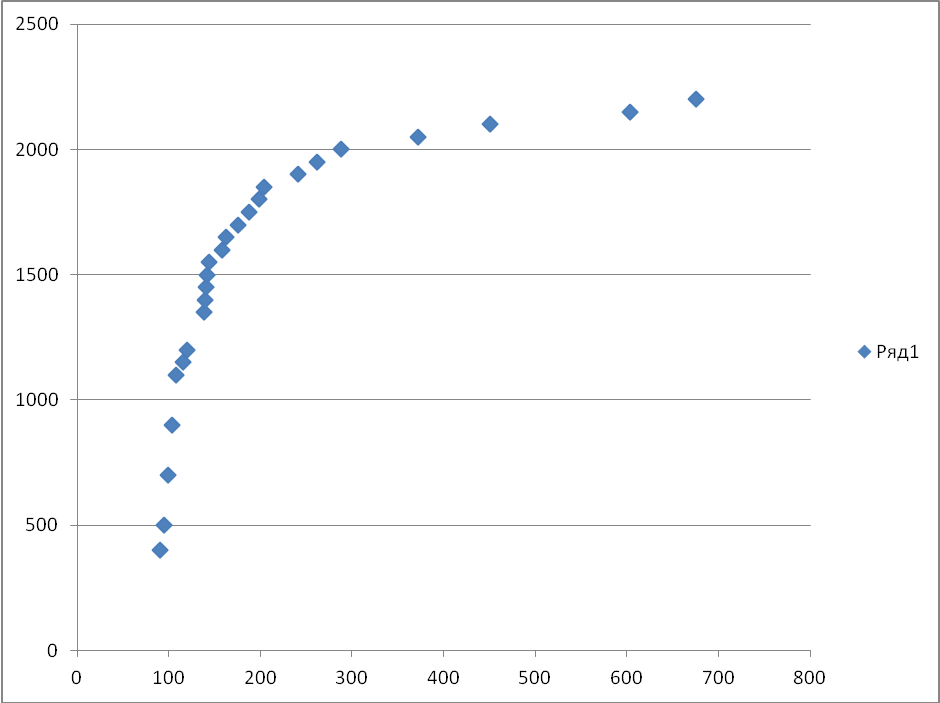
Этап. Вычислим вероятность того, что значение Н превысит 900 .
Значения
![]() и
и
![]() мы находили ранее. Получаем
мы находили ранее. Получаем
![]() ,
,
![]() .
.
Подставляем в формулу:
![]()
