Задание. Провести статистическое исследование зависимости проходки на долото К от глубины Н бурения при резонансной компоновке низа бурильной колонны. Определить вероятность того, что проходка на долото не превысит 100

IЭтап. Произведём первичную обработку опытных данных и сделаем предположение о законе распределения случайной величины н. (в качестве случайной величины я выбрал н).

Данная таблица уже отсортированная по возрастанию.

i	K(х)	H(у)
1	91	400
2	95	500
3	99	700
4	104	900
5	108	1100
6	116	1150
7	120	1200
8	138	1350
9	140	1400
10	141	1450
11	142	1500
12	144	1550
13	158	1600
14	162	1650
15	176	1700
16	188	1750
17	198	1800
18	204	1850
19	241	1900
20	262	1950
21	288	2000
22	372	2050
23	451	2100
24	604	2150
25	676	2200

Видно, что и . Разобьём весь диапазон наблюдаемых значений на 5 интервалов. Длина частичного интервала определяется по формуле: . За начало первого интервала принимаем величину, равную . Тогда .

1.Cоставим интервальный статистический ряд частот т.е. в каждый интервал включаем те размеры , числовые значения которых больше нижней границы интервала и меньше или равны верхней границе. После чего получаем статистический ряд распределения частот ( ), где - число точек , попавших в интервал.

Для получения статистического ряда относительных частот разделим частоты на объём выборки n(n=25).Т.е. .

2.Построим эмпирическую функцию распределения и гистограмму . Значения находится по формуле .

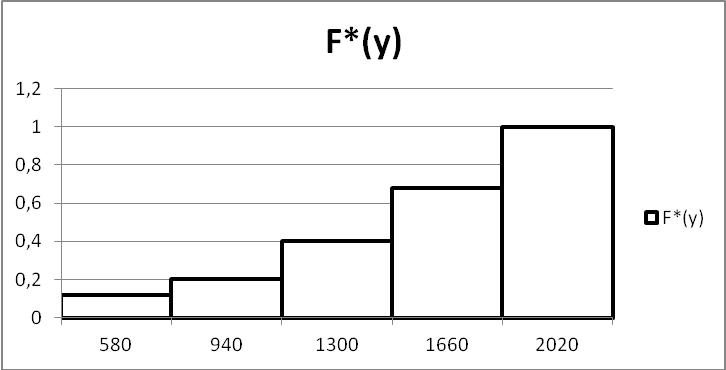
Все расчёты сведём в таблицу:

№	1	2	3	4	5
Интервалы разбиения	[400;760]	]760;1120]	]1120;1480]	]1480;1840]	]1840;2200]
Представитель интервала	580	940	1300	1660	2020
	3	2	5	7	8	25
	0,12	0,08	0,2	0,28	0,32	1
	0,12	0,2	0,4	0,68	1
	0,0003	0,0002	0,00056	0,00078	0,00089

Та же самая таблица полученная в Excel:

	Эмпирические характеристики
Л.Г.	П.Г.	Центр	Частоты	p*i	F*i(y)	f*i(y)
400	760	580	3	0,12	0,12	0,000333
760	1120	940	2	0,08	0,2	0,000222
1120	1480	1300	5	0,2	0,4	0,000556
1480	1840	1660	7	0,28	0,68	0,000778
1840	2200	2020	8	0,32	1	0,000889
			25	1

3.Запишем в общем виде предполагаемый закон распределения исследуемой величины. По виду гистограммы и статистической функции распределения подберём вид теоретических функций распределения и функции плотности вероятности . В данном случае берём распределение арксинуса:

, .

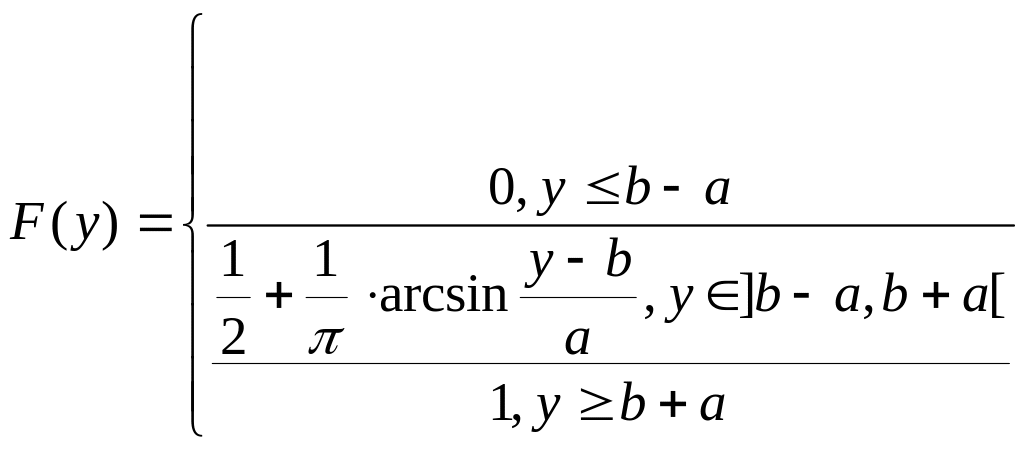2Этап. 1.Вычислим числовые характеристики выборки и определим параметры гипотетического распределения.

-Математическое ожидание: =1516.

-Дисперсия случайной величины: = 245944.

-Среднее квадратичное отклонение: = 495,927.

-Коэффициент вариации: = 32,7%

-Коэффициент асимметрии: = 0,339

-Эксцесс: = -1,12.

-Средние квадратичные ошибки определения асимметрии

=0,445.

и эксцесса =0,792.