17

Лекция № 14

Лекция 14.Дифракция света.

1. Принцип Гюйгенса-Френеля.

Дифракцией света называется явление отклонения света от прямолинейного распространения, когда свет, огибая препятствие, попадает в область своей геометрической тени.

Для решения задачи о распространении световой волны, нужно задать условия на границах, начальные условия (t=0), задать характеристики среды и решить волновое уравнение.

Сделать это очень сложно, поэтому нужен какой-то упрощенный метод решения. Таким методом является метод, основанный на принципе Гюйгенса-Френеля:

Пусть имеется некоторая совокупность источников световых волн. Тогда любую точку пространства, до которой в данный момент времени дошла световая волна (волновой фронт), можно рассматривать как точечный источник вторичных волн, а волновое возмущение в любой точке пространства (вне волнового фронта) представляет собой результат интерференции этих вторичных волн.

Этот же принцип можно выразить также следующим образом.

Р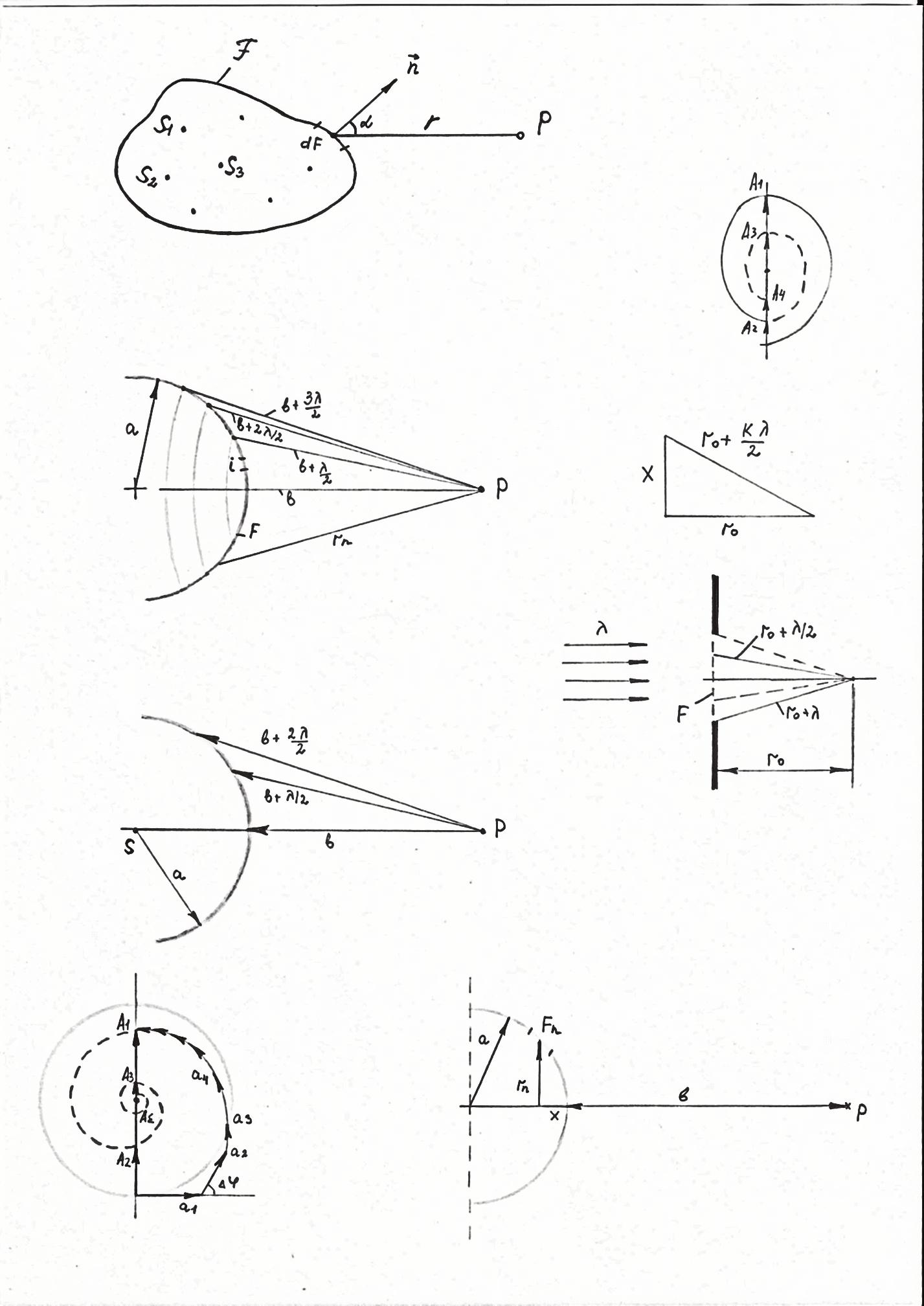 ассмотрим, например, источники света S₁, S₂, … . Если эти источники света окружить произвольной замкнутой поверхностью ℱ, то каждую точку такой поверхности можно рассматривать как источник вторичных когерентных сферических волн. Световое поле, возникающее при интерференции волн, идущих от этих фиктивных источников, вне поверхности ℱ совпадает с полем, создаваемым реальными источниками S₁, S₂, … .

- плоская

- сферическая

Для сферической волны

- возмущение от вторичной сферической волны.

Здесь A₀- амплитуда первичной волны в рассматриваемой точке,

ω – частота колебаний (все источники являются монохроматическими),

r- расстояние от точки на поверхности ℱ до точки наблюдения P,

- некоторая функция угла α между ,

-нормаль к поверхности ℱ;

По гипотезе Френеля =0 при ;

Согласно Кирхгофу .

2. Метод зон Френеля.

Волновая поверхность разбивается на зоны, расстояния от границ которых до точки наблюдения отличаются на величины, кратные , и колебания, создаваемые в точке наблюдения соседними зонами Френеля, будут противоположны по фазе, а возмущения – противоположны по знаку ( .

Рассмотрим для простоты свободно распространяющуюся сферическую волну.

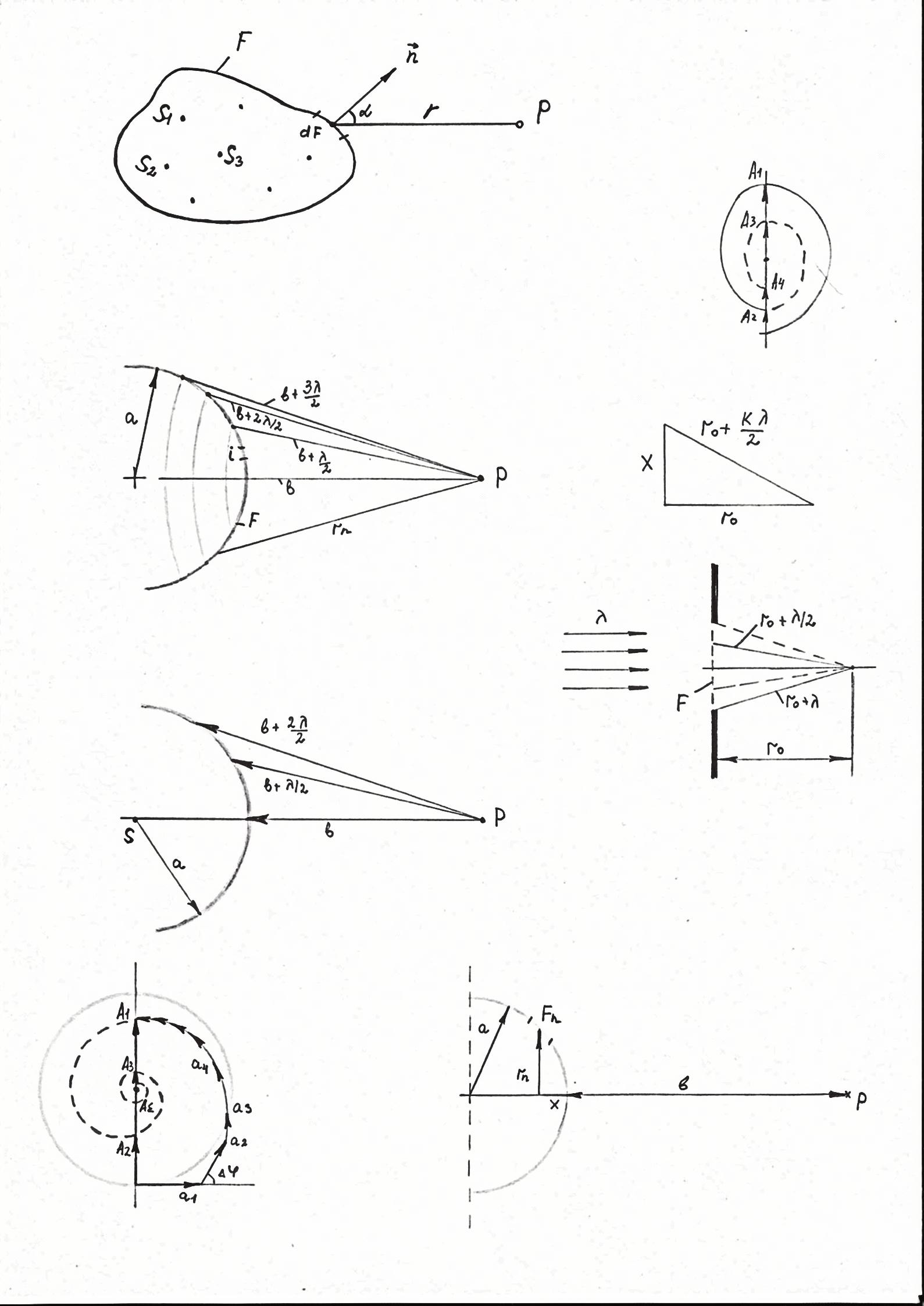
Т.к. убывает при увеличении n, а (при ), то - убывающая функция от n ( , а ).

Таким образом, имеем

.

Приближенно считая, что ,

,

… .

получим .

Считая дополнительно, что , получаем

Амплитуда световой волны в точке наблюдения равно половине амплитуды, создаваемой 1^й зоной Френеля.

3. С пираль Френеля.

Разобьем волновой фронт на зоны Френеля, а каждую зону ещё на n частей. Пусть номер такой части: .

Тогда расстояние от й части первой зоны Френеля до точки наблюдения будет равно , а разность хода между соседними частями . Отсюда – сдвиг фаз.

.

А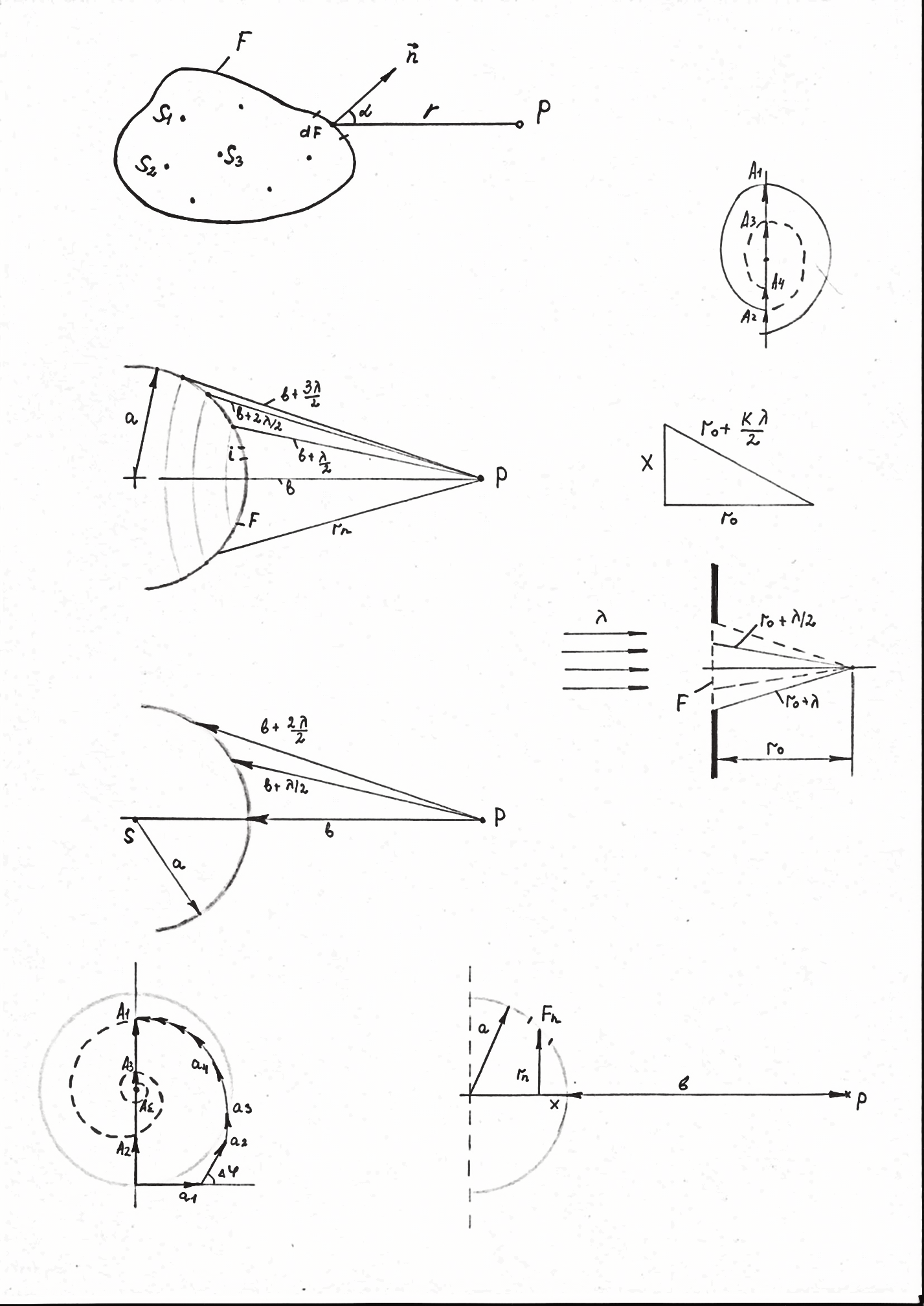 мплитуды колебаний от каждой части можно сложить так же, как при многолучевой интерференции. При этом сдвиг фаз между соседними частями равен , а полный поворот вектора, соответствующий прохождению одной зоны равен . В данном случае при сложении векторов необходимо учесть, что .

Векторная диаграмма сложения колебаний, обусловленных всеми вторичными источниками, расположенными на волновой поверхности, при ∞ разбиении последней и называется спиралью Френеля.

Из векторной диаграммы видно, что освещенность в точке наблюдения при открытии чётного числа зон Френеля будет ослаблена, а при открытии нечётного – усилена. Амплитуда колебаний при открытой лишь первой зоне Френеля будет максимальной и она приблизительно вдвое больше амплитуды результирующего колебания, обусловленного действием всего волнового фронта.

Напомним, что интенсивность света в данной точке пропорциональна квадрату амплитуды колебания.

П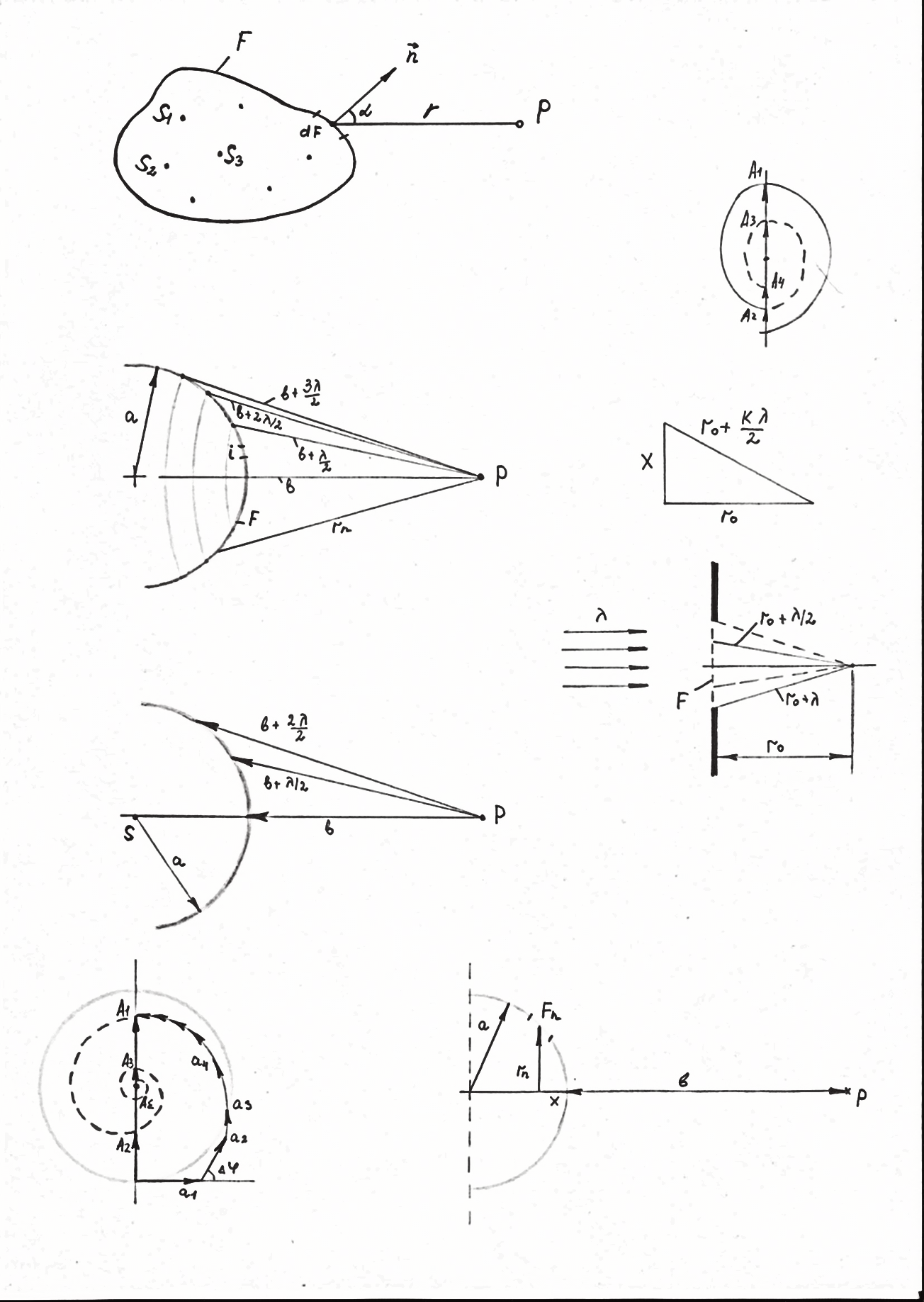 римечание. Для сферической волны радиус - й зоны Френеля

.

Для плоской волны( )

.