Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Российский химико-технологический университет им. Д.И. Менделеева

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Lecture_2_2014

.pdf

Скачиваний:

Добавлен:

13.02.2015

Размер:

801.72 Кб

Скачать

☆

1 / 21 2 > Следующая >>>

Гамильтониан атома с зарядом ядра Z|е| (начало координат на ядре):

H=Tэ(r)+ Vэя(r,R)+ Vээ(r)=

−

∑ i2 −∑

+∑∑

, i≠ j

4πε r

0 i

0 ij

Исключим Vээ

hi χi (ri ) = εi χi (ri )

i =1,2,3,...,N

Ze2

одноэлектронный

= −

i −

4πε r

гамильтониан

0 i

Электрон i описывается волновой функцией

χi (ri

) и имеет энергию ε

Считают, что поведение каждого электрона не зависит от поведения остальных электронов и описывается некоторой волновой функцией подобно единственному электрону в атоме водорода.

В этом суть приближения независимых частиц.

χi (ri ) называются одноэлектронными волновыми функциями или орбиталями.

Полный гамильтониан атома в приближении независимых частиц

	N
	H = ∑hi
	1
Собственная функция Н	Ψ= χ1(r1) χ2(r2) χ3(r3) χN (rN)
(волновая функция Хартри)		Произведение орбиталей
		Произведение орбиталей
Энергия атома	Ψ	H	Ψ = ε1 +ε2 +ε3 +...+εN = E
Энергия атома

		Сумма орбитальных энергий

Метод самосогласованного поля

Действие на данный электрон всех остальных электронов заменяют средним полем. Это дает возможность разделить в сферической системе координат переменные в уравнении Шредингера.

Одноэлектронный гамильтониан:

Ze2

hССП = −

2 −

∑

, j =1,2,3,...,(N-1)

4πε

4πε r

r 2

0 ij

Оператор описывает отталкивание между электронами i

и j, усредненное по всем

положениям электрона j.

Собственная функция гамильтониана:

H = ∑hiССП

есть функция Хартри

Ψ= χ1(r1) χ2(r2) χ3(r3) χN (rN)

Собственные значения Н:

E' = ∑εi

=∑ Ψ|hiССП |Ψ

εi = сумма кинетической энергии i-го электрона, потенциальной энергии его притяжения к ядру и средней потенциальная энергия его отталкивания от

остальных электронов.

Комментарий: необходимо решить систему одноэлектронных уравнений с

гамильтонианом, включающим усредненное межэлектронное

взаимодействие – систему уравнений Хартри. Для этого нужно построить набор

операторов, а прежде - рассчитать усредненные величины	e	2
операторов, а прежде - рассчитать усредненные величины	e
	4πε r
		0 ij j

Как это сделать?

Вероятность того, что электрон j с волновой функцией χj(rj)

находится в бесконечно малом объеме dvj, равна χj 2 dvj.

Отталкивание электрона i, усредненное по всем положениям электрона j, равно:

= e2

∞ χ

2 (r )

dv j

4πε

∫

−∞

Однако, чтобы вычислить этот интеграл,

волновые функции

χ j

(rj ) должны уже быть известны!

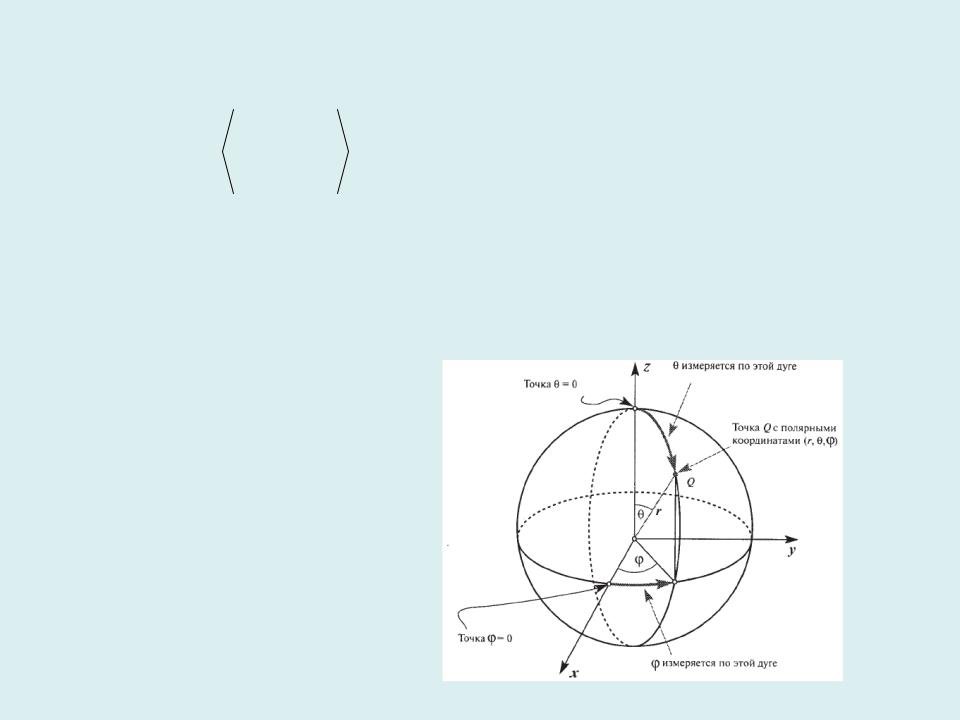
Приближение центрального поля

Потенциал дополнительно усредняют по всем направлениям, интегрируя его по углам θ и ϕ:

N	e2
∑
	4πε		r
		0
j			ij

π 2π

(rj)

∑∫ ∫

χ j

r2sinθ

dθ

dϕ dr

4π

4πε

j j

j,θ ,ϕ

i 0 0

0 ij

Вводимое таким образом приближение центрального поля позволяет рассматривать ССП-решения для любого атома как модифицированные решения для

	Z	e
одноэлектронного водородоподобного атома с потенциалом
	4πε		r.
0
Сферическая симметрия
задачи позволяет переход к
сферической системе координат:
r,θ,ϕ

Потенциальная энергия зависит только от расстояния до ядра, т.е. сила притяжения электрона к ядру носит центральный характер. Поэтому угловой момент электрона относительно ядра постоянен, а волновая функция является собственной функцией не только гамильтониана, но и операторов квадрата углового момента L2 и его проекции Lz.

Переменные в уравнении Шредингера в сферических координатах разделяются, и волновые функции, описывающие состояния электронов атома в r-пространстве (атомные орбитали), имеют вид:

χnlm (r,θ,ϕ) = N(n,l)Rnl (r)Ylm (θ,ϕ)

нормировочный	радиальная	угловая
множитель	часть	часть

n, l и m – главное, орбитальное и магнитное квантовые числа, соответственно.

n =1, 2, 3...	–	главное
l = 0, 1, 2, 3,..., n–1	–	орбитальное
m = –l, –l+1, ..., +l	–	магнитное	7

Атомные орбитали и их характеристики

Радиальное уравнение Шредингера

∂2

2 ∂

−

l(l +1)

R = −

2mE

∂r2

∂r

Его конкретный вид возник после разделения переменных в сферических

координатах. Дает точное значение нормированной

радиальной функции

Rn,l для водородоподобного атома:

2Zr

−

2l+1 2Zr

na0

Rnl (r) = −NZnl

Ln+l

na0

NZnl

нормировочный множитель, зависящий от Z, n и l;

2l+1

2Zr

– присоединенные полиномы Лягерра,

4πε

= 0.529·10–10 м – радиус Бора.

e2m

Радиальные нормированные функции водородоподобных атомов Rnl (r)

n	l																Rnl (r)

1	0																		3										Zr
															Z											−
																						2
																						2
																								e					a0
																													a0
										2
													a0
															3																				Zr
				1								Z																	Zr				−
	0															2
																2																			2a
																																				0
																																				0
				2															1−														e
2				2				a0																				2a0
2
																									5							Zr
						1												Z													−
	1																								2
																									2
																											re					2a0
						2

													6 a0
						3																																		Zr
		2			Z															2Zr												2Z2r2							−
									2
									2
	0												1−															+										e		3a0
	0												1−															+										e		3a0
		3																		3a0												27a				2
		3	3 a0																	3a0												27a				0
										3					Zr													Z2r2									Zr
			8				Z																													−
														2
														2
3																							−											e			3a	0
3	1																						−											e				0
	1	27 6																										6a				2
		27 6			a0										a0													6a				0
																			7												Zr
				4							Z																			−
																					2
																					2
																							r		2	e					3a0
	2
	2		81	30
			81	30							a0

Узлы радиальных функций

R10	R20	R30

1s	2s	3s



	узел		узлы

1 / 21 2 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
13.02.2015645.03 Кб17Lab_Gidravlika.pdf
#
13.02.2015584.43 Кб32Lab_Massoobmen.pdf
#
13.02.2015501.25 Кб9Lab_raboty_po_KKP_Excel.doc
#
13.02.2015648.84 Кб26Lab_Teploobmen.pdf
#
13.02.201550.18 Кб31LECPLAN2.doc
#
13.02.2015801.72 Кб75Lecture_2_2014.pdf
#
31.07.201923.71 Mб27Lektsia_14_Difraktsia_sveta.doc
#
13.02.2015544.5 Кб30Lektsia_3_4_Atom_H.pdf
#
01.03.202537.57 Кб8Lektsia_Struktury_dannykh.docx
#
01.03.20254.64 Mб10lektsii_po_f-kh.doc
#
13.02.201515.73 Mб63Lektsii_TOL.doc