
Вычисление обратной матрицы.
Теорема. Если какая-либо цепочка неособенных строчечных элементарных преобразований переводит квадратную матрицу в единичную матрицу , то матрица обратима и эта же цепочка преобразований переводит матрицу в матрицу .
Доказательство.
Предположим, что
есть цепочка неособенных строчечных
элементарных преобразований, переводящая
квадратную матрицу
в единичную матрицу
.
Тогда,
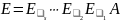 .
.
Отсюда
следует, что матрица
обратима и
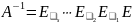 .
.
Из последнего равенства следует, что цепочка неособенных строчечных элементарных преобразований переводит матрицу в матрицу .
Правило
нахождения обратной матрицы: Для
нахождения матрицы, обратной к
-матрице
,
надо прямоугольную матрицу
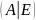 при помощи цепочки неособенных строчечных
элементарных преобразований привести
к виду
при помощи цепочки неособенных строчечных
элементарных преобразований привести
к виду
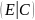 ;
получающаяся при этом матрица
является обратной к матрице
.
;
получающаяся при этом матрица
является обратной к матрице
.
Подстановки.
(Лемма 20.)
Пусть
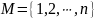 ,
где
– натуральное число.
,
где
– натуральное число.
Определение.
Подстановкой
множества
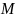 называется инъективное отображение
множества
на себя.
называется инъективное отображение
множества
на себя.
Всякое
отображение
множества
на себя удобно записывать в виде таблицы
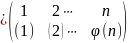 .
Порядок чисел в первой строке несущественен,
его можно как угодно изменить. Однако,
при этом, необходимо, чтобы для всякого
числа
число
.
Порядок чисел в первой строке несущественен,
его можно как угодно изменить. Однако,
при этом, необходимо, чтобы для всякого
числа
число
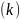 было записано непосредственно под
.
было записано непосредственно под
.
Определение.
Множество всех подстановок множества
обозначается
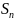 .
Элементы множества
называются подстановками
степени
.
.
Элементы множества
называются подстановками
степени
.
Если
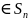 ,
то:
,
то:
- инъективное отображение;
- сюрьективное отображение.
Так как - конечное множество, то из условия 1. следует условие 2. и наоборот.
Произведение
двух подстановок
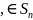 определяется как композиция отображений
определяется как композиция отображений
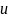 ,
т.е.
,
т.е.
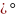 .
Таким образом,
.
Таким образом,
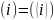 ,
для
,
для
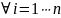 .
.
Теорема.
Алгебра
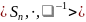 - группа.
- группа.
Доказательство. Так как композиция двух инъективных отображений множества на себя, является инъективным отображением множества на себя, то операция умножения на множестве является алгебраической.
Обозначим через тождественное отображение множества на себя. Тогда - единица множества .
Операция умножения на множестве является ассоциативной, на основании ассоциативности композиции отображений.
Наконец,
для
 существует
существует
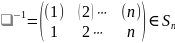 ,
которая является обратным элементом.
,
которая является обратным элементом.
Определение. Группа - называется симметрической группой степени n и обозначается .
Определение. Перестановкой называется всякое упорядоченное расположение элементов множества .
Определение. Два символа перестановки образуют инверсию, если левый символ больше правого символа.
Обозначим
через
 - число всех инверсий перестановки
- число всех инверсий перестановки
 .
.
Определение. Перестановка называется четной, если – четная, в противном случае нечетная.
Определение. Подстановка называется четной, если четности ее перестановок-строк совпадают.
Определение.
Подстановка
вида
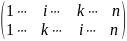 называется транспозицией.
называется транспозицией.
Лемма. Любая транспозиция является нечетной подстановкой.
Доказательство.
Пусть
- транспозиция, переводящая
в
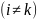 .
Будем полагать, что
.
Будем полагать, что
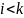 .
Легко видеть, что пара элементов
.
Легко видеть, что пара элементов
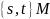 может образовать инверсию, если хотя
бы один из ее элементов есть
или
.
может образовать инверсию, если хотя
бы один из ее элементов есть
или
.
Если
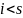 или
или
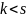 ,
то среди пар
,
то среди пар
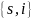 и
и
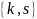 нет инверсий.
нет инверсий.
Если
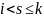 ,
то среди пар
,
то среди пар
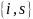 инверсиями являются следующие:
инверсиями являются следующие:
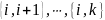 ,
всего
,
всего
 инверсий.
инверсий.
Если
 ,
то среди пар
,
то среди пар
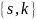 инверсиями являются следующие:
инверсиями являются следующие: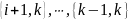 ,
всего
,
всего
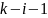 инверсий.
инверсий.
Итак,
транспозиция
содержит всего
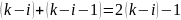 инверсий, следовательно
- нечетная подстановка.
инверсий, следовательно
- нечетная подстановка.
Определение.
Знаком подстановки
называется число равное
 .
.
Определители.
(Лекция 21.)
Пусть
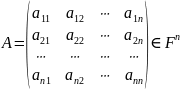
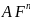 где
- коммутативное кольцо или поле.
где
- коммутативное кольцо или поле.
Рассмотрим
множество всех произведений элементов
матрицы
,
взятых по одному из каждой строки и
каждого столбца. Всякий элемент множества
содержит
сомножителей и может быть записан в
виде
 .
.
Такому
элементу поставим в соответствие
подстановку
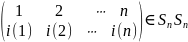 .
.
Верно
и обратное, каждой подстановке
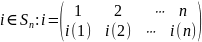 соответствует единственный элемент
множества
соответствует единственный элемент
множества
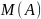 ,
а именно
,
а именно
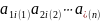 .
.
Таким
образом, отображение
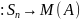 является взаимно однозначным отображением.
является взаимно однозначным отображением.
Определение.
Определителем
матрицы
называется
сумма
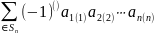 .
.
Сумма
содержит
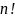 слагаемых, причем каждой подстановке
в этой сумме соответствует в точности
одно слагаемое.
слагаемых, причем каждой подстановке
в этой сумме соответствует в точности
одно слагаемое.
Определитель
матрицы
обозначается:
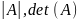 .
.
Если
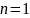 ,
то
,
то
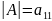 .
.
Если
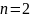 ,
то
,
то
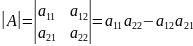 .
.
Если
,
то
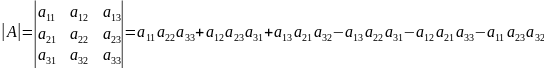 .
.
