
Матрицы и определители.
Операции над матрицами и их свойства.
(Лекция 17.)
В этой главе обозначим
через
 некоторое поле, которое будем называть
полем скаляров. Элементы множества
будем называть скалярами.
некоторое поле, которое будем называть
полем скаляров. Элементы множества
будем называть скалярами.
Определение.
Пусть
 – целые положительные числа. Таблица
– целые положительные числа. Таблица
 с элементами из поля
называется матрицей
над полем
или
с элементами из поля
называется матрицей
над полем
или
 – матрицей над полем
.
– матрицей над полем
.
Коротко матрицу обозначают
 Если
Если
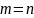 ,
матрицу называют квадратной матрицей
порядка
,
матрицу называют квадратной матрицей
порядка
 .
Множество всех
матриц над полем
обозначают через
.
Множество всех
матриц над полем
обозначают через
 .
В частности, множество всех квадратных
матриц над F
порядка n
обозначают
.
В частности, множество всех квадратных
матриц над F
порядка n
обозначают
 .
.
Обозначение:
 -ая
строка матрицы
-ая
строка матрицы
 обозначается
обозначается
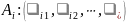 ,
j-ый
столбец матрицы A
обозначается
,
j-ый
столбец матрицы A
обозначается
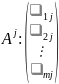 .
.
Определение.
Две
– матрицы
 и
и
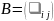 называются равными,
если
называются равными,
если
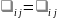 для любых индексов
и
для любых индексов
и
 .
И записывают:
.
И записывают:
 .
.
Определение. Матрица называется нулевой и обозначается O, если все ее элементы равны нулю.
Определение.
Суммой двух
– матриц
и
называется новая
– матрица,
 -й
элемент которой равен
-й
элемент которой равен
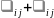 ,
т.е.
,
т.е.
 .
.
Определение.
Произведением скаляра
 на матрицу
называется новая
– матрица,
-й
элемент которой равен
на матрицу
называется новая
– матрица,
-й
элемент которой равен
 ,
т.е.
.
,
т.е.
.
Для матрицы
 выполняется равенство
выполняется равенство
 .
Поэтому матрицу
обозначают также через
.
Поэтому матрицу
обозначают также через
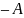 и называют противоположной матрице
.
и называют противоположной матрице
.
Пусть
 и
и
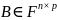 ,
т.е. число столбцов матрицы
равно числу строк матрицы
,
т.е. число столбцов матрицы
равно числу строк матрицы
 .
Определим произведение строки
.
Определим произведение строки
 на столбец
на столбец
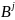 следующим образом:
следующим образом:
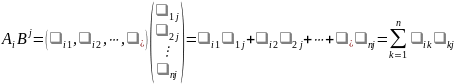 .
.
Определение.
Произведением матриц
и
называется
новая
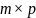 – матрица,
-й
элемент которой равен
– матрица,
-й
элемент которой равен
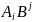 ,
т.е.
,
т.е.
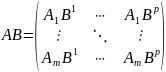 .
.
Теорема.
Умножение матриц ассоциативно, т.е. для
любых матриц
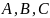 из того, что существуют произведения
из того, что существуют произведения
 и
и
 следует, что
следует, что
 .
.
Доказательство.
Из существования произведения матриц
и
,
по определению 1.1.6. можно считать, что
 .
Следовательно, произведения
.
Следовательно, произведения
 и
и
 существуют и принадлежат множеству
существуют и принадлежат множеству
 .
Пусть
.
Пусть
 и
и
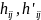 -
-ые
элементы матриц
-
-ые
элементы матриц
 и
и
 соответственно. Докажем, что
соответственно. Докажем, что
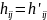 для любых индексов
и
.
В самом деле,
для любых индексов
и
.
В самом деле,
 =
=
 .
.
 .
.
Следовательно, для любых индексов и , т.е. .
Теорема. Операции над матрицами обладают следующими свойствами:
Алгебра
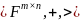 - абелева группа;
- абелева группа;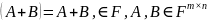 ;
; ;
; ;
;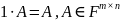 ;
;Умножение матриц ассоциативно;
Умножение матриц дистрибутивно относительно сложения, т.е.
 ,
если произведение
и сумма
,
если произведение
и сумма
 существуют, и
существуют, и
 ,
если произведение
,
если произведение
 и сумма
существуют;
и сумма
существуют;Для любого скаляра и любых матриц
 ,
если произведение
существует.
,
если произведение
существует.
Доказательство. Свойства 1-5 доказываются аналогично доказательству соответствующих свойств сложения векторов и умножения на скаляр векторов арифметических векторных пространств.
По теореме умножение матриц ассоциативно.
Пусть
 .
Легко проверить, что
.
Легко проверить, что
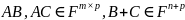 .
Отсюда следует, что
.
Отсюда следует, что
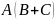 и
и
 –
-матрицы.
–
-матрицы.
Покажем, что -элементы этих матриц равны, т.е.
 ;
;

Следовательно, . Аналогично доказывается, что , если произведение и сумма существуют;
Для
доказательства свойства 8 найдем
-е
элементы матриц
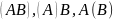 :
:
 ;
;
 ;
;
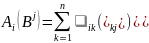 .
.
Эти
три выражения равны между собой в силу
свойств сложения и умножения скаляров.
Следовательно,
 .
.
Транспонирование произведения матриц.
(Лекция 18.)
Определение.
Пусть
 -
-матрица
над полем
.
Тогда
-
-матрица
над полем
.
Тогда
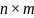 -матрица
-матрица
 ,
такая, что
,
такая, что
 ,
называется матрицей, транспонированной
к матрице
,
и обозначается через
,
называется матрицей, транспонированной
к матрице
,
и обозначается через
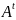 .
.
Таким образом, транспонированная матрица получается в результате замены строк данной матрицы соответствующими столбцами. В частности,
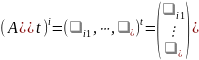 ;
;

Теорема.
Если существует произведение
матриц A
и B,
то существует произведение
 и
и
 .
.
Доказательство.
Предположим, что
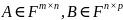 .
Тогда, если
.
Тогда, если
 ,
то
,
то
 .
Кроме того,
.
Кроме того,
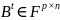 и
и
 .
Следовательно, существует произведение
и
.
Следовательно, существует произведение
и
 .
Таким образом, матрицы
.
Таким образом, матрицы
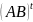 и
являются
и
являются
 -матрицами.
Проверим, что ij-е
элементы соответствующих матриц
-матрицами.
Проверим, что ij-е
элементы соответствующих матриц
 и
и
 этих матриц равны. В самом деле,
этих матриц равны. В самом деле,
 ;
;
с
другой стороны,
 .
.
Следовательно,
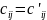 для любых индексов
и
для любых индексов
и
 ,
т.е.
.
,
т.е.
.
Обратимые матрицы.
Пусть
 .
Если
.
Если
 – единичная
– единичная
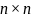 -матрица,
то
-матрица,
то
 .
.
Определение.
Квадратная матрица
называется обратимой,
если существует матрица
,
удовлетворяющая условиям
 и
и
 .
.
Матрица , называется обратной к матрице . Матрицы и называются взаимно обратными.
Лемма. Если матрица обратима, то существует только одна матрица, обратная к .
Доказательство.
Предположим, что
и
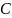 – матрицы обратные к
.
Тогда
– матрицы обратные к
.
Тогда
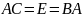 и
и
 ,
т.е.
,
т.е.
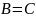 .
.
Если
матрица
обратима, то обратная к
матрица обозначается
 .
Таким образом, для любой обратимой
матрицы выполняются равенства
.
Таким образом, для любой обратимой
матрицы выполняются равенства
 .
.
Множество
всех обратимых
-матриц
над полем
обозначается через

Теорема.
Алгебра
 - группа.
- группа.
Доказательство. Единичная матрица , очевидно, обратима и является нейтральным элементом.
Если – обратимая матрица, то в силу 1.3.1. матрица также обратима.
Множество
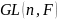 обратимых
-матриц
замкнуто относительно умножения.
Действительно, если
обратимых
-матриц
замкнуто относительно умножения.
Действительно, если
 ,
то
,
то
 ,
т.е. матрица
обратима над
и поэтому принадлежит множеству
.
,
т.е. матрица
обратима над
и поэтому принадлежит множеству
.
Наконец, по теореме умножение матриц ассоциативно.
Следствие. Произведение любого числа обратимых матриц есть обратимая матрица.
Элементарные матрицы.
Определение. Квадратная матрица, получающаяся из единичной матрицы в результате неособенного элементарного преобразования над строками (столбцами), называется элементарной матрицей, соответствующей этому преобразованию.
Так,
например, элементарными матрицами
второго порядка являются матрицы
 ,
где
- любой ненулевой скаляр.
,
где
- любой ненулевой скаляр.
Элементарная матрица получается из единичной матрицы E в результате одного из следующих неособенных преобразований:
Умножение строки (столбца) матрицы E на отличный от нуля скаляр.
Прибавление (вычитание) к какой-либо строке (столбцу) матрицы E другой строки (столбца), умноженной на скаляр.
Обозначим
через
 матрицу, получающуюся из матрицы
в результате умножения
-ой
строки на ненулевой скаляр
:
матрицу, получающуюся из матрицы
в результате умножения
-ой
строки на ненулевой скаляр
:
 .
.
Обозначим
через
 матрицу, получающуюся из матрицы E
в результате прибавления (вычитания) к
i-й
строке j-й
строки, умноженной на ;
матрицу, получающуюся из матрицы E
в результате прибавления (вычитания) к
i-й
строке j-й
строки, умноженной на ;

Через
 ,
будем обозначать матрицу, получающуюся
из матрицы E
в результате применения элементарного
преобразования
над строками; таким образом,
есть матрица, соответствующая
преобразованию .
,
будем обозначать матрицу, получающуюся
из матрицы E
в результате применения элементарного
преобразования
над строками; таким образом,
есть матрица, соответствующая
преобразованию .
Некоторые свойства элементарных матриц:
Свойство. Любая элементарная матрица обратима. Матрица, обратная к элементарной, является элементарной.
Доказательство. Непосредственная проверка показывает, что для любого отличного от нуля скаляра и произвольных i и k выполняются равенства:
 ;
;
 .
.
На основании этих равенств заключаем, что свойство 1 верно.
Свойство. Произведение элементарных матриц является обратимой матрицей.
Свойство.
Если неособенной строчное элементарное
преобразование
переводит
-матрицу
в матрицу B,
то
 .
Верно и обратное утверждение.
.
Верно и обратное утверждение.
Доказательство.
Если
есть умножение i-ой
строки матрицы
 на ненулевой скаляр ,
то
на ненулевой скаляр ,
то
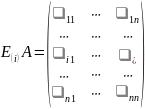
Т.е.
 .
Если же
.
Если же
 ,
то
,
то
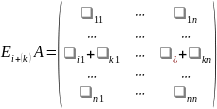
Т.е.
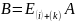 .
Легко проверить, что верно и обратное
утверждение.
.
Легко проверить, что верно и обратное
утверждение.
Свойство.
Если матрица
получается из матрицы
при помощи цепочки неособенных
преобразований
 ,
то
,
то
 .
Верно и обратное утверждение.
.
Верно и обратное утверждение.
Доказательство.
По свойству 3, преобразование
 переводит матрицу A
в матрицу
переводит матрицу A
в матрицу
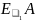 ,
,
 переводит матрицу
в матрицу
переводит матрицу
в матрицу
 ,
и т.д.
,
и т.д.
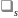 переводит матрицу
в матрицу
.
Что и требовалось доказать.
переводит матрицу
в матрицу
.
Что и требовалось доказать.
Легко проверить и обратное утверждение.
Условия обратимости матрицы.
(Лекция 19.)
Лемма. Квадратная матрица с нулевой строкой (столбцом) необратима.
Доказательство.
Пусть
– квадратная матрица с нулевой строкой,
– любая матрица,
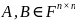 .
Пусть
- нулевая строка
матрицы
;
тогда
.
Пусть
- нулевая строка
матрицы
;
тогда

Т.е. -ая строка матрицы является нулевой. Следовательно, матрица A необратима.
Лемма. Если строки квадратной матрицы линейно зависимы, то матрица необратима. Доказательство. Пусть A – квадратная матрица с линейно зависимыми строками. Тогда существует цепочка неособенных строчечных элементарных преобразований, переводящих матрицу A в ступенчатую матрицу; пусть - такая цепочка. По свойству 4, имеет место равенство:
,
где C – матрица с нулевой строкой. Следовательно, по лемме 1, матрица C необратима. С другой стороны, если бы матрица A была обратимой, то произведение слева в последнем равенстве было бы обратной матрицей, как произведение обратимых матриц, что невозможно. Следовательно, матрица A необратима.
Следствие. Если квадратная матрица обратима, то ее строки линейно независимы.
Лемма. Квадратную матрицу с линейно независимыми строками можно представить в виде произведения элементарных матриц.
Доказательство.
Пусть A
– квадратная матрица с линейно
независимыми строками. Существует
цепочка строчечных неособенных
элементарных преобразований
,
переводящих матрицу A
в единичную матрицу E.
По свойству 4, следует, что
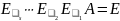 .
Следовательно,
.
Следовательно,
 ,
причем по свойству 1, множители
,
причем по свойству 1, множители
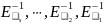 являются элементарными матрицами.
являются элементарными матрицами.
Теорема.
для любой квадратной матрицы
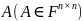 равносильны следующие утверждения:
равносильны следующие утверждения:
Матрица обратима;
Строки (столбцы) матрицы линейно независимы;
Матрицу можно представить в виде произведения элементарных матриц.
Доказательство. Самостоятельно.
