Пример:

Найдите все взаимно обратные пары по сложению в Z₁₀.

Решение

Даны шесть пар аддитивных инверсий — (0, 0), (1, 9), (2, 8), (3, 7), (4, 6) и (5, 5). В этом списке 0 — инверсия самому себе; так же и 5. Обратите внимание: аддитивные инверсии сложения обратны друг другу; если 4 — аддитивная инверсия 6, тогда 6 — также аддитивная инверсия числу 4.

8.Уравнение деления (   ) имеет два входа ( a и n ) и два выхода ( q и r ). В модульной арифметике интересует один из выходов — остаток r. Когда делим a на n значение остатка равно r. Это значит, что можно представить изображение вышеупомянутого уравнения как бинарный оператор с двумя входами a и n и одним выходом r.

Операции по модулю

Вышеупомянутый бинарный оператор назван оператором по модулю и обозначается как mod. Второй вход ( n ) назван модулем. Вывод r назван вычетом (рисунок показывает отношение деления по сравнению с оператором по модулю)

Оператор по модулю ( mod ) выбирает целое число ( a ) из множества Z и положительный модуль ( n ). Оператор определяет неотрицательный остаток ( r ).

Мы можем сказать, что

a mod n = r

Мультипликативная инверсия

В Z_n два числа a и b мультипликативно инверсны друг другу, если

Например, если модуль равен 10, то мультипликативная инверсия 3 есть 7. Другими словами, мы имеем  .

В модульной арифметике целое число может или не может иметь мультипликативную инверсию. Целое число и его мультипликативная инверсия сравнимы с 1 по модулю n .

Может быть доказано, что a имеет мультипликативную инверсию в Z_n, если только НОД(n, a) = 1. В этом случае говорят, что a и n взаимно простые.

Пример 1

Найти мультипликативную инверсию 8 в Z₁₀.

Решение

Мультипликативная инверсия не существует, потому что  . Тоесть нельзя найти число между 0 и 9, такое, что при умножении на 8 результат сравним с 1 по mod 10.

Пример 2

Найти все мультипликативные инверсии в Z₁₀.

Решение

Есть только три пары, удовлетворяющие условиям существования мультипликативной инверсии: (1, 1), (3, 7) и (9, 9). Числа 0, 2, 4, 5, 6 и 8 не имеют мультипликативной инверсии.

Мы можем проверить, что

(1 x 1) mod 10 = 1 (3 x 7) mod 10 = 1 (9 x 9) mod 10 = 1

12.Шифрование симметричными ключами использует единственный ключ и для кодирования и для дешифрования. Кроме того, алгоритмы шифрования и дешифрования — инверсии друг друга.

Моноалфавитный шифр подстановки

Ключ независим от передаваемых букв. Нужно согласовать единственный ключ, который используется, чтобы зашифровать каждую букву в исходном тексте или расшифровать каждую букву в зашифрованном тексте. «а» и «б» могут договориться об отображении для каждой буквы и записать его в виде таблицы. 

Шифр Цезаря, также известный как шифр сдвига — один из самых простых и наиболее широко известных методов шифрования.

Шифр Цезаря — это вид шифра подстановки, в котором каждый символ в открытом тексте заменяется буквой находящейся на некоторое постоянное число позиций левее или правее него в алфавите.

19. Конечное поле — поле с конечным числом элементов — является очень важной структурой в криптографии. Галуа показал что поля, чтобы быть конечными, должны иметь число элементов pn, где p — простое, а n — положительное целое число. Конечные поля обычно называют полями Галуа и обозначают как GF(pn).

Поле Галуа, GF(p n ), — конечное поле с p n элементами.

Поля GF(p в степени n)

В дополнение к полям GF(p) в криптографии мы также интересуемся полями GF(pn). Однако множества Z, Zn, Zn* и Zp, которые мы использовали до сих пор с операциями сложения и умножения, не могут удовлетворить требованиям поля. Поэтому должны быть определены некоторые новые множества и некоторые новые операции на этих множествах. В следующей лекции мы рассматриваем очень полезное в криптографии поле GF(2n).

20. Представление кодов в виде полиномов основано на подобии (изоморфизме) пространства двоичных n - последовательностей и пространства полиномов степени не выше n - 1.

Код для любой системы счисления с основанием Х может быть представлен в виде:

G (x) = an-1 xn-1+ an-2 xn-2+... + a1 x+ a0 = , где аi - цифры данной системы счисления (в двоичной 0 и 1);

х - символическая (фиктивная) переменная, показатель степени которой соответствует номерам разрядов двоичного числа-

Например: Кодовая комбинация 1010110 может быть представлена в виде:

G (x) =1×x6+0×x5+1×x4+0×x3+1×x2+1×x1+0×x0 =x6+x4+x2+x=10101

При этом операции над кодами эквивалентны операциям над многочленами. Представление кодов в виде полиномов используется например, в циклических кодах. Сложение двух полиномов никогда не создает полином, выходящий из множества. Однако умножение двух полиномов может создать полином со степенью большей, чем n – 1. Это означает, что мы должны делить результат на модуль и сохранять только остаток, как мы сделали в модульной арифметике. Для множеств полиномов в GF(2ⁿ) группа полиномов степени n определена как модуль. Модуль в этом случае действует как полиномиальное простое число. Это означает, что никакие полиномы множества не могут делить этот полином. Простое полиномиальное число не может быть разложено в полиномы со степенью меньшей, чем n. Такие полиномы называются неприводимые полиномы

Список неприводимых полиномов
Степень	Неприводимый полином
1	(x+1)x
2	(x2+x+1)
3	(x3+x2+1)(x3+x+1)
4	(x4+x3+x2+x+1)(x4+x3+1)(x4+x+1)
5	(x5+x2+1)(x5+x3+x2+x+1)(x5+x4+x3+x+1)(x5+x4+x3+x2+1)(x5+x4+x2+x+1)

21. Простые и составные числа. Каждое натуральное число, большее единицы, делится по крайней мере на два числа: на 1 и на само себя. Если число не имеет делителей, кроме самого себя и единицы, то оно называется простым, а если у числа есть еще делители, то составным. Единица же не считается ни простым числом, ни составным. Например, числа 7, 29 — простые; числа 9, 15.

Если число меньше ста, то, скорее всего мы сразу сможем ответить на этот вопрос. Однако с большими числами дело сложнее. Возьмем, например, число 2009. Простое оно или составное? Попробуем найти возможные делители этого числа среди первых простых чисел. 2009 определенно не делится на 2 (так как оно нечетное), на 3 (так как сумма его цифр 2+9=11 не делится на 3 ), на 5. А вот, попробовав разделить 2009 на 7, мы увидим, что в результате получается целый результат – 287. Таким образом, получен ответ: число 2009 – составное. В данном случае ответ получен достаточно быстро. Бывает, что проверка на простоту производиться гораздо дольше, а для работы с большими целыми числами требуются даже специальные компьютерные программы.

ОТА. Любое составное число можно составить из некоторого количества простых с помощью умножения. Например, составное число 2009 можно получить так:

2009 = 7 * 7 * 41

В математике рассматривается так называемая основная теорема арифметики, которая утверждает, что любое натуральное число ( n>1 ) либо само является простым, либо может быть разложено на произведение простых делителей, причем единственным способом (если не обращать внимания на порядок следования сомножителей).

Воспользовавшись обозначением степени, разложение числа 2009 на простые множители можно записать так:

2009 = 72 * 41

Разложение на множители называется каноническим, если все множители являются простыми и записаны в порядке возрастания.

Например, запишем каноническое разложение числа 150 на множители:

150 = 2 * 3 * 52

16. Шифр Хилла — полиграммный шифр подстановки, основанный на линейной алгебре. Лестер С. Хилл изобрел этот шифр в 1929, и это был первый шифр, который позволял на практике оперировать более чем с тремя символами за раз. Последующее обсуждение шифра предполагает начальные знания матриц.

Шифрование:

Каждой букве сперва сопоставляется число. Для латинского алфавита часто используется простейшая схема: A = 0, B =1, ..., Z=25, но это не является существенным свойством шифра. Блок из n букв рассматривается как n-мерный вектор и умножается на n × n матрицу по модулю 26. Матрица целиком является ключом шифра. Матрица должна быть обратима в , чтобы была возможна операция расшифрования.

Для того, чтобы расшифровать сообщение, необходимо обратить шифротекст обратно в вектор и затем просто умножить на обратную матрицу ключа.

17. Шифр, преобразования из которого изменяют только порядок следования символов исходного текста, но не изменяют их самих, называется шифром перестановки (ШП). Простой перестановочный шифр с фиксированным периодом n подразумевает разбиение исходного текста на блоки по n символов и использование для каждого такого блока некоторой перестановки E. Ключом такого шифра является используемая при шифровании перестановочная матрица P или вектор t, указывающий правило перестановки. Таким образом, общее число возможных ключей определяется длиной блока n и равно n!. При дешифрации используется матрица обратной перестановки D, являющаяся обратной к матрице P по умножению, то есть D*P=I, где I — единичная матрица.

Современные блочные шифры обычно являются ключевыми шифрами подстановки, в которых ключ позволяет только частичные отображения возможных входов информации в возможные выходы. Однако эти шифры обычно не проектируются как единый модуль. Чтобы обеспечивать требуемые свойства современного блочного шифра, такие как рассеяние и перемешивание информации (обсуждается кратко), этот шифр формируется как комбинация модулей транспозиции (называемых P -блоками), модулей подстановки (называемых S -блоками) и некоторыми другими модулями (обсуждается кратко).

P -блок (блок перестановки) подобен традиционному шифру транспозиции символов. Он перемещает биты. В современных блочных шифрах мы можем найти три типа P -блоков: прямые P -блоки, P -блоки расширения и P -блоки сжатия

18. Алгебраическая система или алгебраическая структура — множество G (носитель) с заданным на нём набором операций и отношений (сигнатура), удовлетворяющим некоторой системе аксиом. Понятие алгебраической системы родственно понятию универсальной алгебры.

n-арная операция на G — это отображение прямого произведения n экземпляров множества в само множество . По определению, 0-арная операция — это просто выделенный элемент множества. Чаще всего рассматриваются унарные и бинарные операции, поскольку с ними легче работать. Но в связи с нуждами топологии, алгебры, комбинаторики постепенно накапливается техника работы с операциями большей арности, здесь в качестве примера можно привести теорию операд (клонов полилинейных операций) и алгебр над ними (мультиоператорных алгебр).

Определение 1. Множество G, снабжённое операцией .・., условно называемой умножением1,

называется группой, если эта операция обладает следующими свойствами:

1) для любых трёх элементов выполняется равенство f ・ (g ・ h) = (f ・ g) ・ h (ассоциативность);

2) существует такой элемент e ∈ G, что e ・ g = g ・ e = g для любого g ∈ G (существование

единицы)2;

3) для любого элемента g ∈ G существует такой элемент g−1 ∈ G, что g ・ g−1 = g−1 ・ g = e

(существование обратного элемента).

Группа называется коммутативной (или абелевой), если f ・ g = g ・ f для всех f, g ∈ G.

Подмножество H ⊂ G называется подгруппой в G, если из f, g ∈ G следует, что f ・ g ∈ G.

10.Матрицы вычетов

Криптография использует матрицы вычетов: матрицы могут содержать все элементы из Zn. Все операции на матрицах вычетов выполняются так же, как и на матрицах целых чисел, за исключением того, что операции производятся в модульной арифметике. Есть одно интересное свойство: матрица вычетов имеет мультипликативную инверсию, если детерминант матрицы имеет мультипликативную инверсию в Zn. Другими словами, матрица вычета имеет мультипликативную инверсию, если НОД (det (A), n) = 1.

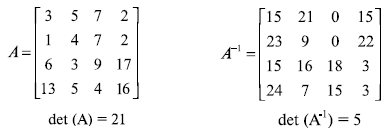
Рисунок 3.8 показывает матрицу вычетов в Zn и его мультипликативной инверсии A-1. Возьмем детерминант det (A) = 21, который имеет мультипликативную инверсию 5 в Z26. Обратите внимание, что когда мы умножаем эти две матрицы, то результат — единичная матрица мультипликативная матрица, в Z26.