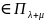- •Пространство элементарных событий.
- •Операции над событиями.
- •Аксиома теории вероятности.
- •Наивероятнейшее число успехов.
- •Числовые характеристики св.
- •Дисперсия св.
- •Начальный и центральный моменты.
- •Основные законы распределения дсв.
- •Основные законы распределения нсв.
- •Числ хар-ки системы св. Начальный и центральный моменты сис св.
- •Придельные теоремы тв.
Основные законы распределения дсв.
1)Выражденное распределение.
Говорят, что СВ Х имеет выражденное распред с параметром а, если она может принять един знач x=a с вероятностью 1. M(x)=a; D(x)=0
2)Распределение Бернулли.
Говорят,
что СВ Х имеет распределение Бернуллис
параметром p (x≤Вр),
если она может принять 2а значения 0 и
1 с вероятностями p и q. Т.е. СВ Х есть
число появлений некоторого события в
одном испытании по схеме Бернулли с
вероятностью успеха р. g(t)=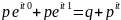 ;
M(x)=0*q+1p=p;
D(x)=(0-p)2q+(1-p)2p=
p2q+q2p=pq(p+q)=pq.
;
M(x)=0*q+1p=p;
D(x)=(0-p)2q+(1-p)2p=
p2q+q2p=pq(p+q)=pq.
3)Биноминальное распределение.
Говорят,
что СВ Х распределена по биноминальному
закону с параметрами n и p, если она может
принять одно из своих возможных значений
m с вероятностью P(x=m)=Pn(m)=Cnmpnqn-m,
q=1-p;
m=0,n.
Т.е. СВ Х есть число появлений некот
события в n
испытаниях по схеме Бернулли при
вероятности появления события при
испытании=р. M(x)=1/i*q’(0);
g’(t)=n(q+peit)n-1pieit;
g’(0)=inp(q+p)n-1=inp;
M(x)=np;
D(x)=npq;
σ= =
= ;
A=
;
A= ;
E=
;
E=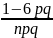 .
.
4)Геометрическое распределение.
Говорят,
что СВ Х имеет геом рапред с парам р,
если СВ может принять одно из своих
возможных значений m=1,2,3…
с вероятностью P(x=m)=pqm-1,
где q=1-p.
M(x)= m-1=p
m-1=p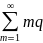 m-1=
p
m-1=
p m)’=
p(
m)’=
p(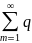 m)’
=p(
m)’
=p( )’=
p
)’=
p 2=p/p2=1/p;
D(x)=q/p2;
A=
2=p/p2=1/p;
D(x)=q/p2;
A= ;
E=
;
E= 2.
2.
5) Закон Пуассона.
Говорят. Что СВ ξ распред по з Пуассона с парам λ>0, если вероятность того, что СВ ξ примет опред значен m. P(ξ=m)=Pm=λme-λ/m!, где ь=0,1,2… З.Пуассона явл пределной формой биноминального распред, при n->∞, p->0. g(t)=eλ(eit-1)-характер ф-ия; M{ξ}=1/i*g’(0)=λ; D{ξ}=λ
Основные законы распределения нсв.
1)З.равномерной плотности.
Говорят,
что ξ равномерно распределена на отрезке
[a,b],
ξ
V[a,b],
если ее плотность распред вероятности
постоянна на этом отрнзке: f(x)=
1/b-a,
x
[a,b];
0, x F(x)=
=0,
x≤a;
F(x)=
=0,
x≤a;
 ,
a≤x≤b;
1, x>b.
M{ξ}=
,
a≤x≤b;
1, x>b.
M{ξ}= =
=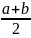 ;
D{x}=(b-a)2/12;
σ=
;
D{x}=(b-a)2/12;
σ= ;
A=0; E=-1,2. Вероятность
попадания в интервал [a,b]:
P(α≤ξ≤β)=F(β)-F(α)=
;
A=0; E=-1,2. Вероятность
попадания в интервал [a,b]:
P(α≤ξ≤β)=F(β)-F(α)= .
.
2) Показательное распределение.
Говорят,
что ξ распред по показ закону с парам
α>0, если ее плотность распред выгляди
след образом: f(x)=αe-αx,
x≥0;
0, x<0.
F(x)= -αtdt=
-e-αt|0x=
1-e-αt,
x≥0;
0, x<0.
g(t)=M(eitx)=
-αtdt=
-e-αt|0x=
1-e-αt,
x≥0;
0, x<0.
g(t)=M(eitx)= -αteitxdx=
-αteitxdx= e(it-α)x|0∞=
e(it-α)x|0∞= .
M{ξ}=
.
M{ξ}=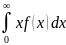 =
= -αxdx=|u=x;
du=dx;
dv=e-αx;
v=-1/2e-αx
|=2[-x/α*e-α|0∞-
-αxdx=|u=x;
du=dx;
dv=e-αx;
v=-1/2e-αx
|=2[-x/α*e-α|0∞-
 -αx)dx]=1/2e-αx|0∞=1/2;
D{ξ}=M{ξ2}-M2{ξ};
M{ξ2}=
-αx)dx]=1/2e-αx|0∞=1/2;
D{ξ}=M{ξ2}-M2{ξ};
M{ξ2}= 2e-αxdx=2/α2.
D{ξ}=
2e-αxdx=2/α2.
D{ξ}= 2=1/α2.
σ=1/2;
A=2;
E=6.
2=1/α2.
σ=1/2;
A=2;
E=6.
3) Нормальный закон распределения.
Говорят,
что ξ распред по норм закону с парам
α
R,
σ>0, если плотность распред имеет вид:
f(x)=
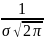 *exp{-(x-α)2/2σ2},
x
R.
M{ξ}=
=
*exp{-(x-α)2/2σ2},
x
R.
M{ξ}=
=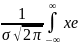 -(x-α)^2/2σ^2dx=
|
-(x-α)^2/2σ^2dx=
| =t;
x=
=t;
x= σt+α;
dx=
σdt|=
σt+α;
dx=
σdt|=
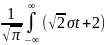 e-t^2dt=
e-t^2dt= e-t^2dt+
e-t^2dt+ -t^2dt=0+
-t^2dt=0+ =α;
D{ξ}=
=α;
D{ξ}=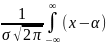 2e-(x-α)^2/2σ^2dx=
|x-α=
2e-(x-α)^2/2σ^2dx=
|x-α=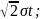 dx=
σdt|=
dx=
σdt|=
 2t2*
2t2*
e-2σ^2t^2/2σ^2*
σdt=1/ 2t2dt=2σ2/
2t2dt=2σ2/ 2e-t^2dt=|u=t;
du=dt;
dv=te-t^2dt;
v=-e-t^2|=σ2.
A=0;
E=0.
2e-t^2dt=|u=t;
du=dt;
dv=te-t^2dt;
v=-e-t^2|=σ2.
A=0;
E=0.
СВ
распред по норм закону с парам 0 и 1 наз
стандартной норм величиной. a=0;
σ2=1.
Плотность вероятности f0,1(x)=1/ *e
*e .
Функция распределения F0,1(x)=1/
.
Функция распределения F0,1(x)=1/ dx.
dx.
Функция СВ.
Теорема1.
ξ-НСВ, Fξ(x),
fξ(x)?=,
кот дифференцируема и монотонна, тогда
ф-ия плотности СВ
 =φ(ξ)
можно записать fη(x)=|φ-1(x)’|*fξ(φ-1(x))
=φ(ξ)
можно записать fη(x)=|φ-1(x)’|*fξ(φ-1(x))
Доказ.
Предположим φ(x)
возрастающ ф-ия =>
 φ-1(x)
=> ф-ия распределена Fη(x)=Fφ(ξ)(x)=P(φ(ξ)<x)=P(ξ<
φ-1(x))=Fx(φ-1(x))=
φ-1(x)
=> ф-ия распределена Fη(x)=Fφ(ξ)(x)=P(φ(ξ)<x)=P(ξ<
φ-1(x))=Fx(φ-1(x))= =|t=
φ-1(z);
=|t=
φ-1(z);
dt=(φ-1(z))’dz;
t=
φ-1(z);
z=x|=
η=φ(ξ):
fη(x)-|(
φ-1(x))’|*fξ(φ-1(x))=
Следствие.
Если ξ и η=φ(ξ)
ДСВ, то рядраспред СВ η
может быть получен непосредственно
путем подсчета вероят значений величины
ξ. З(η=yR)=
Системы СВ.
Совокупность СВ X={X1,X2,…Xn} заданных на одном пространстве наз случайным вектором. Ф-ия распред n-мерного случ вектора наз ф-ей вида: Fx(x1,x2,..,xn)=P(X1<x1, Xi<xi,…,Xn<xn)
Свойства
ф-ии распред.
1) ;
2)
;
2)
 ;
;
 ;
F(∞,y)=P(x<∞,Y<y)=
1*P(Y<y)=
;
F(∞,y)=P(x<∞,Y<y)=
1*P(Y<y)=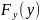 ;
3)
;
3)
 F(∞;∞)=P(X<∞,
Y<∞)=1;
4)P(a≤x≤b,
c≤y≤d)=F(b,d)-F(b,c-[F(a,d)-F(a,c)].
F(∞;∞)=P(X<∞,
Y<∞)=1;
4)P(a≤x≤b,
c≤y≤d)=F(b,d)-F(b,c-[F(a,d)-F(a,c)].
Говорят,
что случ вектор {x,y}
имеет дискр распред, если множество
значений пар его компонент (Xi,Yi)-конечно
и
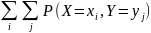 =1
=1
Табл содержащая перечень возможных комбинаций знач векторок и соответствующих им вероятностей наз табл совместного распред.
Гов,
что случ вектор имеет непрер распред,если
сущ неотр ф-ия
 >0,что
для
>0,что
для
 ;
fxy(x,y)-плотность
совместного распред.
;
fxy(x,y)-плотность
совместного распред.
Свойства
плотности распред.
1)fxy(x,y)≥0;
2)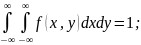 3)
3) ;
4) P((x,y)
;
4) P((x,y) )=
)= P(a≤x≤b,
c≤y≤d)
=
P(a≤x≤b,
c≤y≤d)
= ;
5)Если x
и y
имеет непрер совмест распред, то каждое
из этих величин также имеет непрер
распред, причем: f(x)=
;
5)Если x
и y
имеет непрер совмест распред, то каждое
из этих величин также имеет непрер
распред, причем: f(x)= ;
f(y)=
;
f(y)=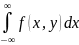 .
.
Независимость СВ.
СВ
x1,x2,…xn
наз независимыми, если для
x1,x2,…xn
выполняется равенство: F(X1,X2,…Xn)= .
.
ДСВ
X1,X2,…Xn
независимы, если для
x1,x2,…xn
P(X1=x1,
Xi=xi,…,Xn=xn)=
 .
.
НСВ
X1,X2,…Xn
независимы, если для
x1,x2,…xn
выполняется
равенство: f(x1,x2,…xn)= .
.
Усл
плотностью распред величины X,
входящей в систему {X,Y},
при усл, что величина У приняла опред
значение у, назф-ия
 =
= .
.
Ф-ия двух СВ. Задача композиции.
Пусть
{X,Y},
Z=φ(X,Y),
φ(X,Y)-неслучайная
ф-ия, тогда
 =P(Z<z)=
=P(Z<z)=
 ,{X,Y}-дискр
распр;
,{X,Y}-дискр
распр;
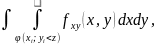 {X,Y}-непрер
распр.
{X,Y}-непрер
распр.
M{
φ(X,Y)}= ДСВ
ДСВ
M{
φ(X,Y)}= ДСВ
ДСВ
Задача
комбинации-это
задача поред з.распред СВ по известным
законам самих величин. Теорема1(Фор
свертки).Ели СВ Х,У-независимые СВ и
имеют непрер распред с плотностями
 ,
,
 ,
то
,
то
 .
Доказ.
.
Доказ.
 .
Теорема2.
Если X
и Y
независимы, P(x+y=Zk)=
.
Теорема2.
Если X
и Y
независимы, P(x+y=Zk)= .
Теорема3.
Если X
и Y
независимы и X
.
Теорема3.
Если X
и Y
независимы и X ,
то Z=X+Y,
Z
,
то Z=X+Y,
Z .
Теорема4.
Если X
и Y
независимы и X
.
Теорема4.
Если X
и Y
независимы и X Y
Y ,
то Z=X+Y
,
то Z=X+Y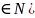 .
Распред наз устойчивым
по суммированию, если сумма 2ч величин
из одного и того же распред имеет то же
распред. Теорема5.
Если Xи
Y-независимы,
X
.
Распред наз устойчивым
по суммированию, если сумма 2ч величин
из одного и того же распред имеет то же
распред. Теорема5.
Если Xи
Y-независимы,
X ;
Y
;
Y ,
то Z=X+Y
,
то Z=X+Y .
Теорема6. Если Xи
Y
независимы, X
.
Теорема6. Если Xи
Y
независимы, X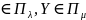 ,
то Z=X+Y
,
то Z=X+Y