
- •Пространство элементарных событий.
- •Операции над событиями.
- •Аксиома теории вероятности.
- •Наивероятнейшее число успехов.
- •Числовые характеристики св.
- •Дисперсия св.
- •Начальный и центральный моменты.
- •Основные законы распределения дсв.
- •Основные законы распределения нсв.
- •Числ хар-ки системы св. Начальный и центральный моменты сис св.
- •Придельные теоремы тв.
Пространство элементарных событий.
Испытание-осущ.какого-либо комплекта усл,кот может быть воспроизведено сколько угодно большее число раз.
Событие-1)явление, кот.могут в результате испытаний произойти или не произойти. 2)любое подмнож.пространства элем.событий [A,B,C].
Пространство элементарных событий –множ.всех моментов исходов испытаний, таких что в ходе испыт.может произойти одно из них.
Достоверные события-событие, кот.происходят неизбежно в данном опыте.
Невозможные события-события, кот.в результате данного опыта произойти не могут.
Совместное/несовместное событие-событие А и В наз.совместными (несовмест), если в результате эксперемента возможно (невозможно) их совместное осуществление.
Говорят,что
событие А влечет
событие В,если при наступлении события
А неизбежно событие В [А В].
В].
События А и В наз.эквивалентными, если А В и В А.
А противоположные события-событие А, в том, что событие А не происходит.
Неикол.группа события-несколько событий в данном опяте образ, если в результате должно произойти непременно одно из них.
Если при проведении опыта могут произойти несколько событий и каждое из них по объективным условиям не является более возможным, чем другое, то такие события называются равновозможными.
Операции над событиями.
Суммой событий А и В наз.событие С,кот. Означает насступление хотя бы одного из событий А и В.
А+В=В+А;
A+Ω= Ω; A+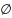 =A;
A+A=A; A+A= Ω; ∑Ai= Ω
=A;
A+A=A; A+A= Ω; ∑Ai= Ω
Произведением А и В наз.событие С, кот.означает осущ-ие обоих событий А и В [С=АВ=А В].
AB=BA; A*Ω=A; A* = ; A*A=A; A*A= ; если А и В несовмест=>АВ= .
Разностью А и В наз С, кот.означает что происходит событие А и не происходит событие В. [С=А\В=А-В]
(А+В)+С=А+(В+С); (AB)C=A(BC); (A+B)*C=AC+BC; A=A; A+B=A*B; AB=A+B; A-B=AB.
Вероятность события-численная мера степени объяктивной возможности этого события.
Подходы: 1.Статическое опред вероятности. Результат наступления или ненаступления события А. если произошло наступление события А m раз, то отношение w=m/n, наз. относит. частотой события А.
2.Статической
вероят события А
наз.придел
к кот.стремится относительная частота
w(A) при неограниченном увеличении
количества испытаний. P(A)= .
.
3.Вероятность на дискретном пространстве элементарных исходов.
Пусть Ω есть пространство элем.исходов,т.е. содержит конечное число элем или счетное количество элем Ω={w1, w2, …, wn}.
Поставим
каждому элем wi Ω в соответствие
число,кот обоз p(wi)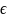 [0,1],
так что ∑p(wi)=1
b
наз вероят
элем исхода. Вероятностью
события А
Ω
наз число P(A)=∑p(wi),
где wi
А. Свойства: 0≤P(A)≤1;
P(Ω)=1;
P(
)=0;
P(A)=1-P(A);
если A
B,
то P(A)≤P(B);
P(A+B)=P(A)+P(B)-P(AB).
Если А и В несовместимые, то P(A+B)=P(A)+P(B).
[0,1],
так что ∑p(wi)=1
b
наз вероят
элем исхода. Вероятностью
события А
Ω
наз число P(A)=∑p(wi),
где wi
А. Свойства: 0≤P(A)≤1;
P(Ω)=1;
P(
)=0;
P(A)=1-P(A);
если A
B,
то P(A)≤P(B);
P(A+B)=P(A)+P(B)-P(AB).
Если А и В несовместимые, то P(A+B)=P(A)+P(B).
4.Классическое опред вероятности.
Пусть
Ω-есть конечное множ равномерных
исходов. P(wi)=1/n,
где n-|
Ω |-число элем множ Ω. Тогда P(A)= ,
где m=|А|-число
элем множ А.
,
где m=|А|-число
элем множ А.
Исход наз благоприятным некот события,если появление этого исхода влечет за собой появление события (m). Вероят события А будем наз отношение m к общему числу n-всех возможных исходов испытания. P(A)=m/n.
5.Основные формулы комбинаторики.
1)формула для числа перестановок. Пусть имеется n различных элем, из кот формир выборки, отличающиеся порядком элем. Получающиеся т.о. комбинации наз перестановками из n элементов. Полное число таких выборов опред по форм: Pn=n*(n-1)(n-2)…2*1=n!
2)формула
для числа размещений без повторений.
Из гр.содержащей n различ элем отбираютя
m элем и размещаются в порядке их
появления. Появляющиеся т.о. комбинации
наз размещением
из n элем по m элем.
(Anm):
 n!/(n-m)!
n!/(n-m)!
3)формула
для числа сочетаний без повторений.Из
гр. содержащей n различных элем отбираются
m различ элем без учета порядка элем.
Получающиеся т.о. комбинации наз
сочетаниями
из n элем по m элем:
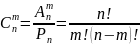
4)формула для числа размещений с повторениями. Из гр. содержащей n различных элем отбираются m различ элем и размещаются в порядке их появления,при чем каждый последующий элем выбирается из полной группы. Получающиеся т.о. комбинации наз размещения с повторениями, а полное число таких выборок опред по форм: nm.
5)формула
для числа сочетаний с повторениями. Из
гр. содержащей n различных элем отбираются
m различ элем без учета порядка элем-ов,
при чем каждый последующий элем
выбирается из полной группы. Получающиеся
т.о. комбинации наз сочитание из n
элем по m
элем с повторениями:

6.Геометр. опред вероятности.
Пусть
пространством элем событий явл некая
область Ω Rn,
при чем все ее точки равноправны, т.е.
если наугад выбрать т. из Ω, то вероятность
ее попадания в обл А не зависит от
расположения от располож А внутри Ω,
а зависит только от меры множ А.
P(•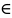 A)=M(A)/M(Ω)
A)=M(A)/M(Ω)
