1.вектор — это элемент векторного пространства (или иначе: линейного пространства). геометрический объект, характеризуемый направлением ( т.е. заданной с точностью до параллельности прямой и направлением на ней) и длиной. Векторы можно складывать и умножать на число. Вектор также можно представить в виде линейной комбинации других векторов. 

Модулем (длиной) вектора называется длина соответствующего направленногоотрезка AB и обозначается как/АВ/

Дваненулевых вектора называются коллинеа́рными, если они лежат на параллельных прямых или на одной прямой. Допусти́м, но не рекомендуется, синоним — «параллельные» векторы. Коллинеарные векторы могут быть одинаково направлены («сонаправлены») или противоположно направлены (в последнем случае их иногда называют «антиколлинеарными» или «антипараллельными»).

Три вектора (или большее число) называются компланарными, если они, будучи приведенными к общему началу, лежат в одной плоскости.Необходимым и достаточным условием компланарности 3-х векторов.есть условие abc=0

Понятие вектор в геометрии отлично от определяемого в алгебре. Различают понятие свободного и связанного (приложенного, закреплённого) вектора.

Связанный вектор или направленный отрезок — упорядоченная пара точек евклидова пространства.

Свободный вектор — класс эквивалентности направленных отрезков.При этом два направленных отрезка считаются эквивалентными, если они:

1. коллинеарны

2. равны по длине

3. одинаково направлены (сонаправлены)

Существует естественный изоморфизм свободных векторов и параллельных переносов пространства (каждый перенос взаимно однозначно соответствует какому-то свободному вектору). На этом также строят геометрическое определение свободного вектора, просто отождествляя его с соответственным переносом.

Большую роль играют векторы в изучении бесконечно малых трансформаций пространства.

2.Действия над векторами

Сумма. Суммой векторов a и b называется такой третий вектор c, что при совмещенных началах этих трех векторов, векторы a и bслужат сторонами параллелограмма, а вектор c -- его диагональю 

Приизведение.Произведением вектора a на вещественное число  называется вектор b, определяемый условием

1)    и, если   , то еще двумя условиями:

2) вектор b коллинеарен вектору a;

3) векторы b и a направлены одинаково, если   , и противоположно, если   .  Разность. Разностью векторов a и b называется сумма   .  Разность обозначается а-в, то есть а-в=а+(-в)

Правило параллелограмма

Сложение векторных величин производится по правилу параллелограмма: сумма двух векторов   и  , приведенных к общему началу, есть третий вектор  , длина которого равна длине параллелограмма, построенного на векторах   и  , а направлен он от точки A к точке B

Правило многоугольника

Правило многоугольника применяется, если нужно найти сумму трех или большего числа векторов.  Сумма нескольких векторов не зависит от того, в каком порядке они складываются. От произвольной точки О отложен вектор   затем от точки А отложен вектор   и, наконец, от точки В отложен вектор   В результате получается вектор 

3.Координаты вектора

Координа́ты ве́ктора ― коэффициенты единственно возможной линейной комбинации базисных векторов в выбранной системе координат, равной данному вектору.

где   — координаты вектора

Свойства

Равные векторы в единой системе координат имеют равные координаты

Координаты коллинеарных векторов пропорциональны:

Подразумевается, что координаты вектора b не равны нулю.

• Квадрат длины вектора равен сумме квадратов его координат:

При умножении вектора на действительное число каждая его координата умножается на это число:

При сложении векторов соответствующие координаты векторов складываются:

Скалярное произведение двух векторов равно сумме произведений их соответствующих координат:

Векторное произведение двух векторов можно вычислить с помощью определителя матрицы

где

Аналогично, смешанное произведение трех векторов можно найти через определитель

4.Скалярное произведение. Угол между векторами

Скалярным произведением двух ненулевых векторов а и b называется число, равное произведению длин этих векторов на косинус угла между ними.

 т. е. скалярное произведение двух векторов равно модулю одного из них, умноженному на проекцию другого на ось, сонаправленную с первым вектором.

  Угол между векторами 

5.Условие параллельности и перпендикулярности векторов

Условия параллельности

КОЛЛИНЕАРНЫЕ ВЕКТОРЫ

- векторы, параллельные одной плоскости. Необходимым и достаточным условием компланарности трех векторов

является равенство:

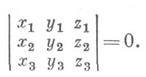
Условия перпендикулярности

Векторы перпендикулярны при к1= -1/к2

6.Уравнение прямой на плоскости Уравнение прямой с угловым коэффициентом

у = kx + b

Уравнение прямой в отрезках

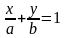
Общее уравнение прямой

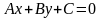
Уравнение прямой с данным вектором нормали

и проходящей через данную точку

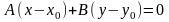
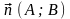
Уравнение с данным направляющим вектором и проходящей через данную точку

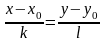
7. Векторное параметрическое уравнение прямой в пространстве:

2

где  — радиус-вектор некоторой фиксированной точки M₀, лежащей на прямой,  — ненулевой вектор, коллинеарный этой прямой,  — радиус-вектор произвольной точки прямой.

Параметрическое уравнение прямой в пространстве:

где  — координаты некоторой фиксированной точки M₀, лежащей на прямой;  — координаты вектора, коллинеарного этой прямой.

Каноническое уравнение прямой в пространстве:

где  — координаты некоторой фиксированной точки M₀, лежащей на прямой;  — координаты вектора, коллинеарного этой прямой.

Общее векторное уравнение прямой в пространстве:

Поскольку прямая является пересечением двух различных непараллельных плоскостей, заданных соответственно общими уравнениями:

и

то уравнение прямой можно задать системой этих уравнений:

8. Прямые  линии в пространстве могут быть параллельными, пересекающимися и скрещивающимися.