3. Теорема про ортогоналізацію.
Твердження. В сепарабельному евклідовому просторі всяка ортогональна система не більша за злічену.
Доведення
Дійсно,
можна дану систему
вважати не тільки ортогональною, а й
нормованою (інакше її б можна було
замінити системою
).
При цьому
=
,
якщо
.
Розглянемо
сукупність куль
.
Ці кулі не перетинаються. З того, що
простір сепарабельний, слідує, що в
ньому існує зліченна, всюди щільна
множина
.
Якщо зліченна множина
всюди щільна в R,
то в кожній такій кулі є хоча б один
елемент з
.
Звідси, число таких куль (а значить і
елементів
)
не більше, ніж злічене.
Теорема (про ортогоналізацію)
Нехай
f ,…,f ,… (8)
- лінійно незалежна система елементів в евклідовому просторі R.
Тоді в просторі R існує система елементів
,…,
,…,
(9)
що задовольняє таким умовам:
Система (9) ортогональна і нормована;
Кожний елемент являє собою лінійну комбінацію елементів
f
,…,f
:
=
+…+
,
причому
0;
Кожен елемент
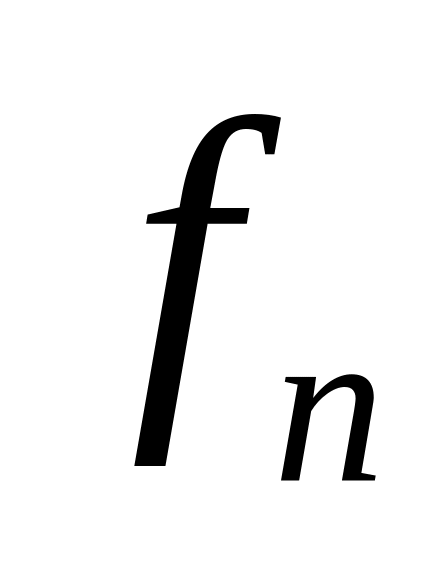можна подати у вигляді
=
+…+
,
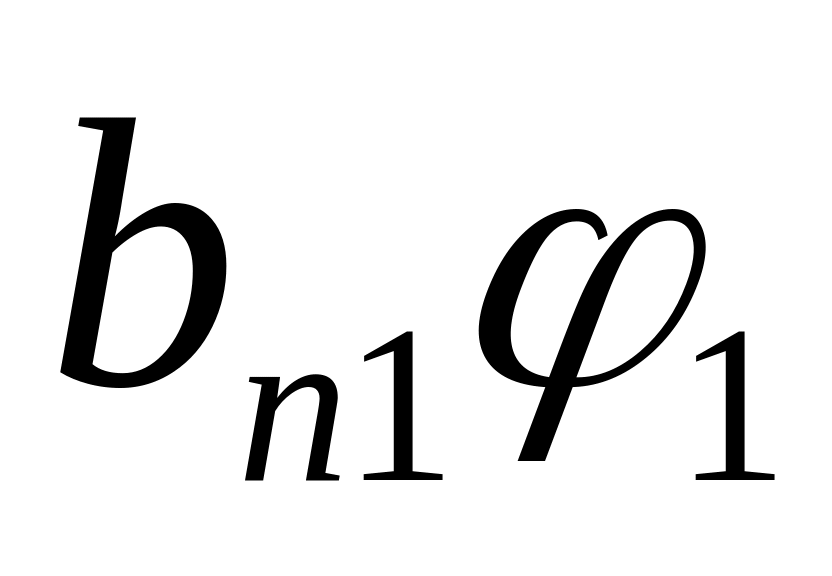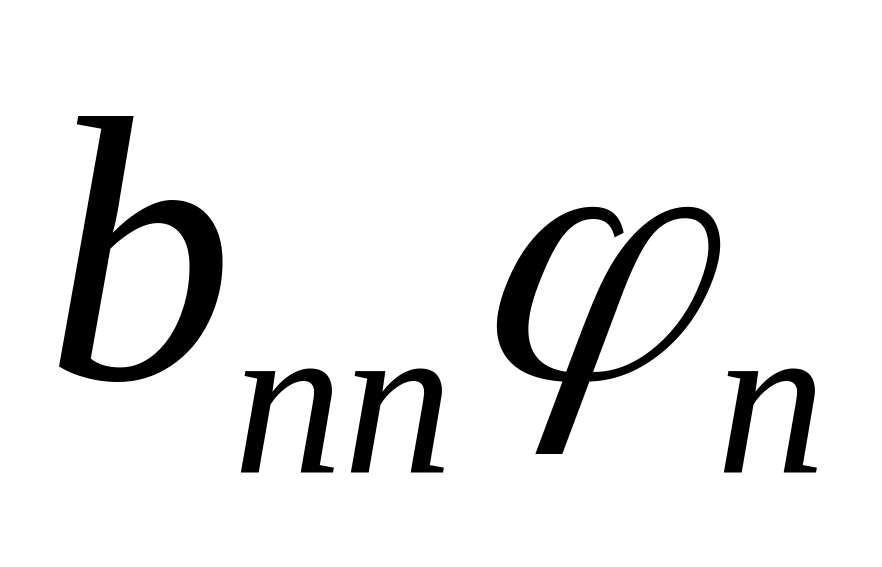причому
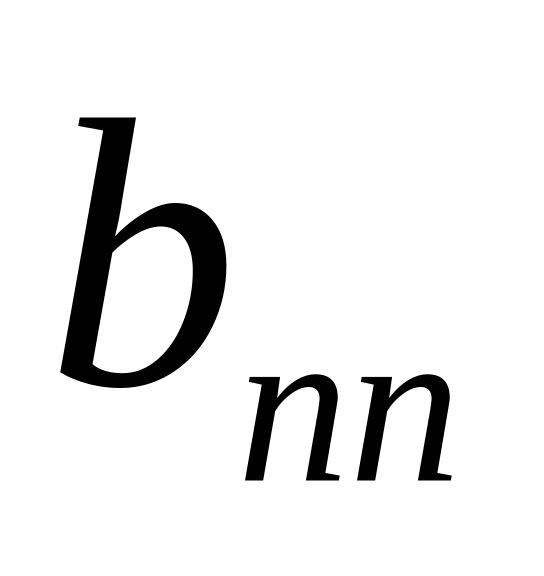0.
Кожен
елемент системи (9) визначається умовами
1.-3. однозначно з точністю до співмножника
.
Доведення
Елемент
знаходимо у вигляді
=
;
при цьому
визначається з умови
=
=1,
звідки
=
=
.
Ясно, що визначається цим однозначно (з точністю до знака).
Нехай
елементи
(k<n),
що задовольняють умовам 1.-3., вже
побудовані. Тоді f
можна подати у вигляді f
=
,
де
=0
при k<n.
Дійсно, відповідні коефіцієнти
,
а значить, і елемент
однозначно визначається з умов:
=
=
=0.
Очевидно,
що
>0,
припущення
=0
було б супротивним лінійній незалежності
системи (8).
Візьмемо
=
.
З індуктивної побудови ясно, що , а звідси, і виражаються через f ,…,f , тобто
=
+…+
,
де
.
Крім того,
=1,
=0
(k<n)
і
=
+…+
,
тобто
задовольняє умовам теореми.
Перехід від системи (8) до системи, що задовольняє умовам 1-3, називається процесом ортогоналізації. Підпростори, породжені системами (8) і (9), співпадають між собою, звідси ці системи повні, але не повні одночасно.
Наслідок. В сепарабельному евклідовім просторі R існує ортогональний нормований базис.
Дійсно,
нехай
-
злічена всюди щільна множина в R.
Виберемо з неї повну систему лінійно
незалежних елементів
.
Для цього достатньо з послідовності
виключити всі ті елементи
,
кожен з яких можна виразити лінійною
комбінацією
з i<k.
Вживаючи процес ортогоналізації до
такої повної системи лінійно незалежних
елементів, ми будуємо ортогональний
базис.
4. Нерівність Бесселя. Замкнені ортогональні системи. Рівність Парсеваля.
Вибравши
в евклідовім n-вимірному
просторі ортогональний нормований
базис е
,…,е
,
можна кожен вектор x
записати
у вигляді
,
(10)
де
.
(11)
Розглянемо,
як узагальнити розклад (10) на випадок
евклідового нескінченновимірного
простору. Нехай
,…,
,…
- ортогональна нормована система в
евклідовому просторі R,
і f
– довільний елемент з R.
Співвіднесемо елементу f
послідовності
чисел
(12)
які назвемо координатами або
коефіцієнтами Фур’є
елемента f
по системі {
}
та ряд (поки що формальний)
,
(13)
який назвемо рядом Фур’є елемента f по системі { }.
Чи буде ряд (13) збіжний, тобто чи прямує послідовність його часткових сум (по метриці простору R) до якої-небудь границі і якщо він збіжний, чи співпадає його сума з вихідним елементом f?
Спочатку
при заданому n
спробуємо підібрати коефіцієнти
так, щоб відстань між f
і сумою
(14)
була мінімальною. Обчислимо цю відстань. Оскільки система ортогональна і нормована, то
=
=
+
=
=
+
=
+
.
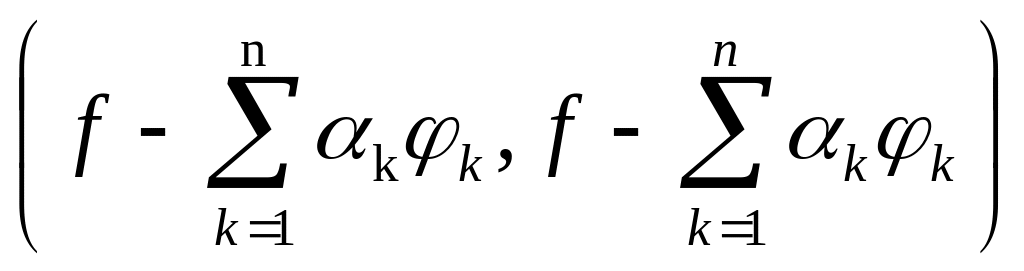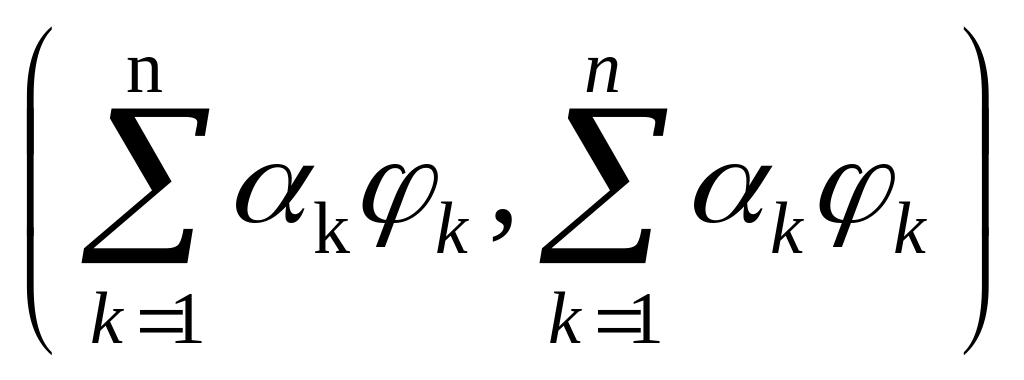Мінімум цього виразу досягається, коли останній доданок дорівнює нулю, тобто при
=
.
(15)
В цьому випадку
=
.
(16)
Показали, що серед усіх сум виду (14) при даному n найменше відхиляється від f частково сума ряду Фур’є елемента f.
Геометрично
це можна пояснити так. Елемент
,
ортогональний всім лінійним комбінаціям
виду
,
тобто ортогональний підпростору,
породженому елементами
,
в тому і тільки в тому випадку, коли
виконується умова (15).
Таким чином, цей висновок являє собою узагальнення відомої теореми геометрії: довжина перпендикуляра, який опущено з даної точки на пряму чи площину, менша за довжину будь-якої похилої, проведеної з цієї ж точки.
Оскільки
завжди
,
то з рівності (16) випливає, що
.
Тут n
– довільне, а права частина не залежить
від n;
звідси ряд
збіжний, і
.
(17)
Ця нерівність називається нерівністю Бесселя. Геометрично вона означає, що сума квадратів проекцій вектора f на взаємно ортогональні напрямки не більша за квадрат довжини самого вектора f.
Означення:
Ортогональна нормована система
називається замкненою,
якщо для будь-якого f
R
справедлива рівність
= , (18)
що називається рівністю Парсеваля.
З
тотожності (16) випливає, що замкненість
системи
рівносильна тому, що для кожного f
R
часткові суми ряда Фур’є
збіжні до f.
Поняття замкненості ортогональної нормованої системи тісно пов’язані з повнотою системи.
Теорема:В сепарабельному евклідовім просторі R всяка повна ортогональна нормована система є замкненою, і навпаки.
Доведення.Нехай
система {
}
замкнена; тоді який би не був елемент
f
R
, послідовність числових сум його Фур’є
збігається до f.
Це значить, що лінійні комбінації
елементів системи {
}
всюди щільні в R,
тобто система {
}
повна. Обернено, нехай система {
}
повна, тобто будь-який елемент f
R
можна скільки завгодно точно апроксимувати
лінійною комбінацією
елементів системи {
};
часткова сума
ряду Фур’є дає не менш точну апроксимацію.
Звідси, ряд
збіжний і рівність Парсеваля виконується.
Ми показали існування повних ортогональних нормованих систем у сепарабельному евклідовім просторі. Оскільки для ортогональних нормованих систем поняття замкненості і повноти співпадають, то існування замкнених ортогональних систем у R не треба доводити, а наведені приклади повних ортогональних нормованих систем є водночас і прикладами замкнених систем.
Ми
припускали, що всі ортогональні системи
нормовані. Переформулюємо поняття
коефіцієнтів Фур’є, ряду Фур’є і таке
інше для будь-яких ортогональних систем.
Нехай {
}
– довільна ортогональна система. За
нею можна побудувати нормовану систему,
що складається з елементів
=
.
Для будь-якого f
R
маємо с
=
=
(
);
=
=
,
де
=
=
.
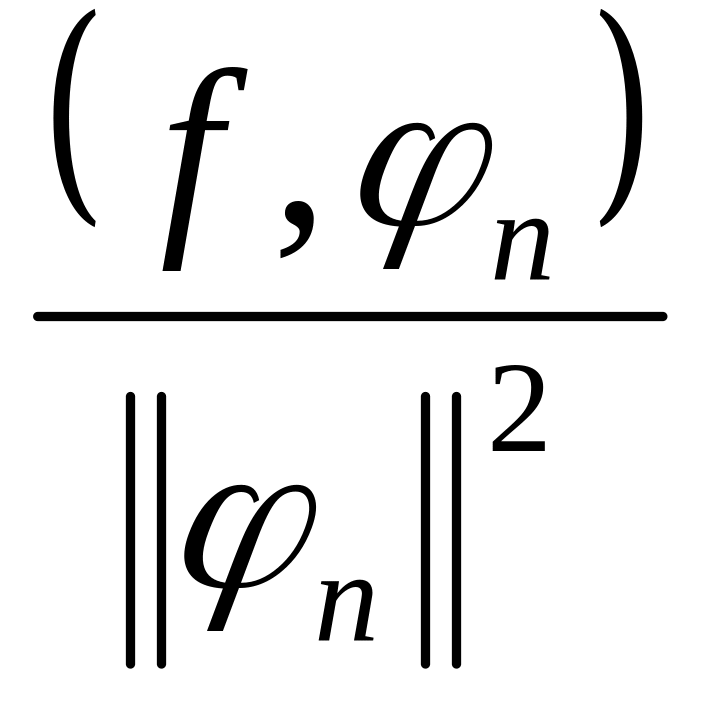(19)
Коефіцієнти
,
що визначаються формулою (19), назвемо
коефіцієнтами Фур’є елемента f
по ортогональній (ненормованій) системі
{
}.
Підставимо в нерівність (17) замість с
їх вирази с
=
з (19) одержимо
(20)
- нерівність Бесселя для довільної ортогональної системи.