
Тема: Евклідові простори.
1.Скалярний добуток. Нерівність Коші-Буняковського. Приклади.
Існує добре відомий спосіб введення норми в лінійному просторі – це задати в ньому скалярний добуток.
Означення:
Скалярним
добутком
у дійсному лінійному просторі
![]() є дійсна функція
є дійсна функція
![]() ,
визначена для кожної пари елементів
,
визначена для кожної пари елементів
![]() і яка задовольняє наступним умовам:
і яка задовольняє наступним умовам:
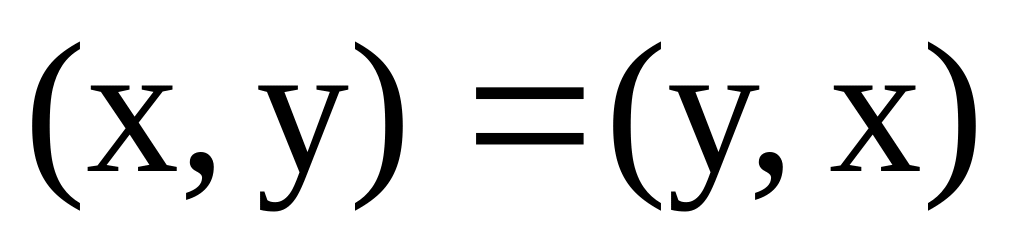 ;
;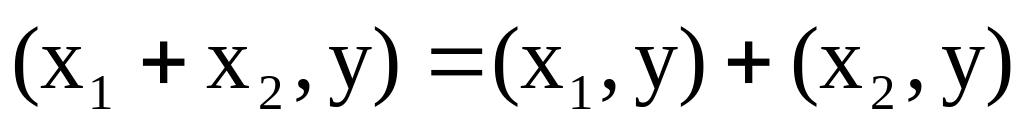 ;
;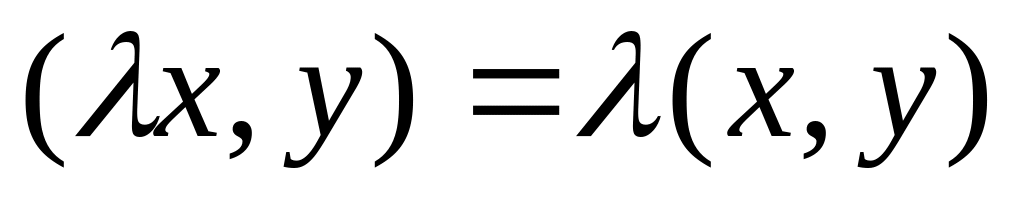 ;
;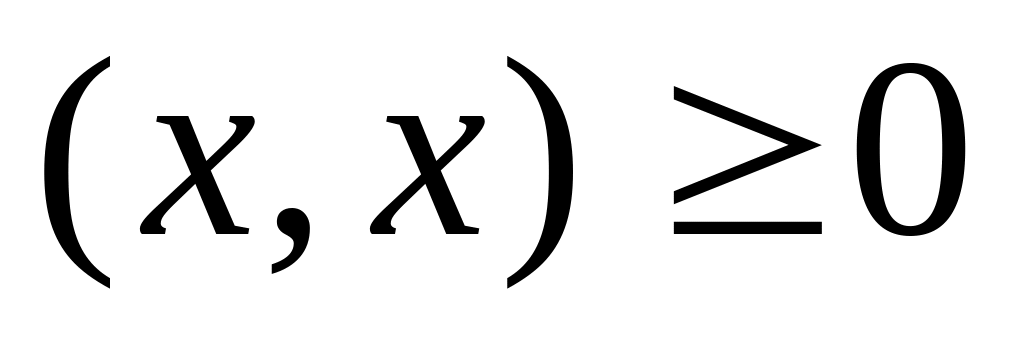 ,
причому
,
причому
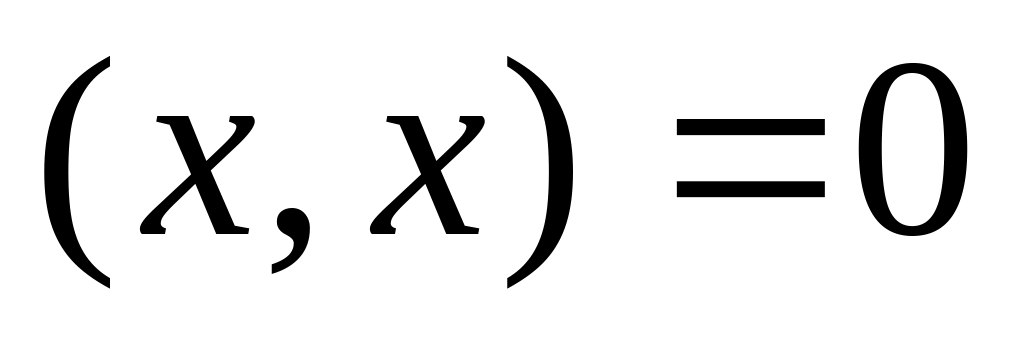 тільки
при
тільки
при
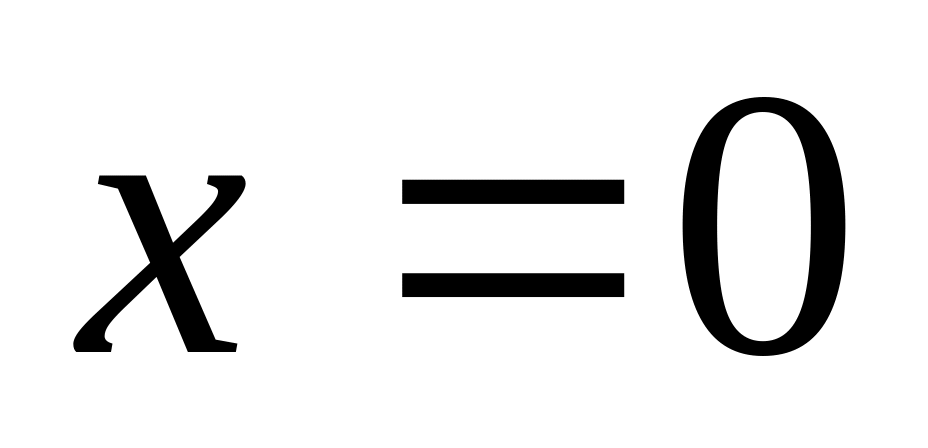 .
.
Означення: Лінійний простір з фіксованим у ньому скалярним добутком називається евклідовим простором.
В
евклідовім просторі
вводиться норма за допомогою формули
![]() .
.
Можна показати, що всі аксіоми норми в цьому випадку виконуються:
1.
![]() виконується,
виконується,
![]() ;
;
2.
![]() ;
;
3. Щоб довести аксіому 2) норми(нерівність трикутника) використаємо нерівність Коші-Буняковського
![]()
![]() .
(1)
.
(1)
Доведемо нерівність Коші-Буняковського (1).
Розглянемо
функцію
![]() .
Тому що вона представляє квадрат деякого
вектора, то
.
Тому що вона представляє квадрат деякого
вектора, то
![]() ,
отже дискримінант квадратного трьохчлена
,
отже дискримінант квадратного трьохчлена
![]() .
.
Знайдемо дискримінант:
D
= 4![]() ,отже
,отже
![]()
![]()
![]()
![]()
![]() .
.
Доведемо
аксіому 2) норми, що
![]()
![]()
Теорема.
В евклідовому просторі сума, добуток
на число і скалярний добуток неперервні,
тобто, якщо
![]() і
і
![]() (збіжність за нормою),
(збіжність за нормою),
![]() (як числова послідовність), то
(як числова послідовність), то
![]() ,
,
![]() та
та
![]() .
.
Доведення. Доведення цих фактів засновано на використанні нерівності Коші-Буняковського:
1)
![]()
Дійсно,
за
![]()
![]()
![]()
![]() ,
,
![]()
за
![]()
![]() ,
,
![]()
тоді
![]()
![]() :
:
![]() ,
,
![]() .
.
2)![]() =
=![]()
![]() +
+![]()
![]()
![]() =
=![]() ,
для великих
,
для великих
![]() .
.
Дійсно,
з того, що
![]() збігається до
збігається до
![]() , слідує, що послідовність
обмежена, тобто
, слідує, що послідовність
обмежена, тобто
![]() :
:![]() (
(![]() ).
Для великих
можна зробити так, щоб
).
Для великих
можна зробити так, щоб
![]() та
та
![]() .
.
3)
![]() =
=
=![]() ,
для великих
,
де
,
для великих
,
де
![]() -
таке число, що
-
таке число, що
![]() (послідовність
(послідовність
![]() збіжна, тому що з того що
слідує
збіжна, тому що з того що
слідує
![]() .
.
2. Ортогональні системи.
Скалярний добуток в R дозволяє ввести в цьому просторі не тільки норму (тобто довжину) вектора, але і кут між векторами; кут між векторами х і у визначається за формулою
cos![]()
![]() (2)
(2)
При
цьому з нерівності Коші-Буняковського
випливає, що вираз, який стоїть в (2)
праворуч, по модулю не більший за 1 і,
звідси, формула (2) дійсно, для будь-яких
ненульових
![]() і
і
![]() визначає деякий кут φ: 0
φ
π.
визначає деякий кут φ: 0
φ
π.
Означення:
Якщо
![]() ,
то з (2) одержимо, що φ=
,
то з (2) одержимо, що φ=![]() ;
в цьому випадку вектори
і
називають
ортогональними.
;
в цьому випадку вектори
і
називають
ортогональними.
Система
ненульових векторів
![]() з
з
![]() називається
ортогональною, якщо
називається
ортогональною, якщо
![]() ,
,![]() =0
при α
=0
при α![]() β.
β.
Твердження: Якщо вектори ортогональні, то вони лінійно незалежні.
Доведення.
Дійсно,нехай
![]()
![]() +
+![]()
![]() +…+
+…+![]()
![]() =0;
оскільки
=0;
оскільки
![]() - ортогональна система, маємо
(
- ортогональна система, маємо
(![]() ,
+…+
)=
,
+…+
)=![]() (
(![]() ,
)=0,
але (
,
)
0
і звідси
=0
для всіх і=1,2,…,n.
,
)=0,
але (
,
)
0
і звідси
=0
для всіх і=1,2,…,n.
Означення:
Якщо
ортогональна система
![]() - повна (тобто найменший замкнений
простір, що її містить, є весь
),
то вона називається ортогональним
базисом.
- повна (тобто найменший замкнений
простір, що її містить, є весь
),
то вона називається ортогональним
базисом.
Взагалі, якщо система (повна або ні) така, що
![]()
то вона
називаєься ортогональною
нормованою (або ортонормованою)
системою.
Якщо
-
ортогональна система, то
![]() -
ортогональна нормована система.
-
ортогональна нормована система.
Означення: Якщо ортогональна система повна та норма кожного її елемента дорівнює одиниці, то вона називається ортогональним нормованим базисом.
Приклади.
Розглянемо деякі приклади евклідових просторів і ортогональних базисів в них.
n-вимірний арифметичний простір
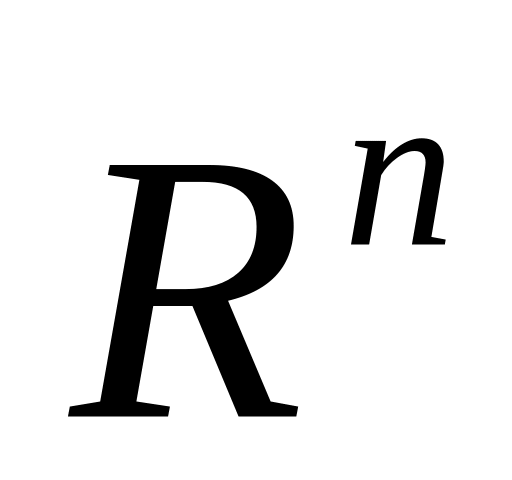 ,
елементами якого є системи дійсних
чисел
,
елементами якого є системи дійсних
чисел
х=(х![]() ,…,х
,…,х![]() )
зі звичайними операціями додавання і
множення на число і скалярним добутком
)
зі звичайними операціями додавання і
множення на число і скалярним добутком
![]() (3)
(3)
являє собою приклад евклідового простору. Ортогональний нормований базис у ньому (один з нескінченого числа можливих) утворюють вектори
е =(1,0,…,0),
е![]() =(0,1,…,0),
=(0,1,…,0),
……………..
е =(0,0,…,1).
Простір
 з елементами х = (х
,…,х
,…),
де
з елементами х = (х
,…,х
,…),
де
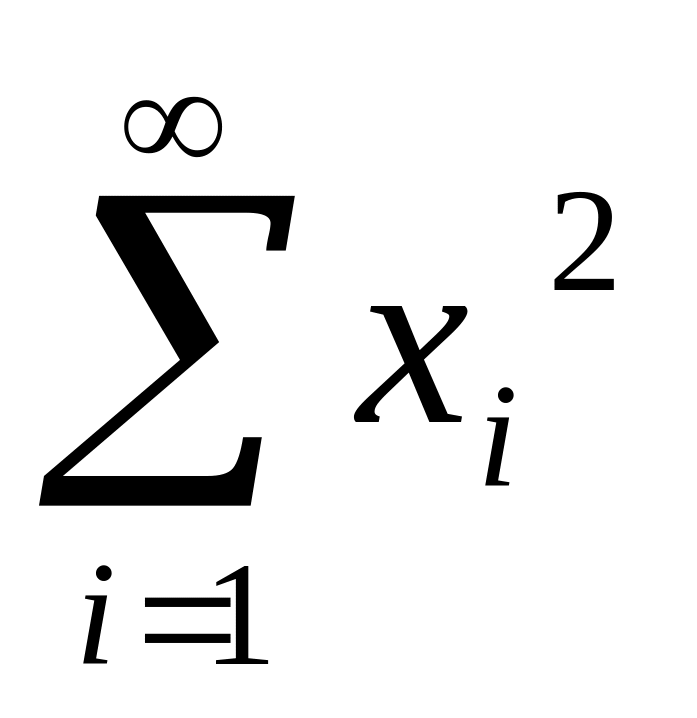 <
< ,
і скалярним добутком
,
і скалярним добутком
![]() (4)
(4)
евклідів простір.
Дійсно,
збіжність ряда, що стоїть в (4) праворуч
випливає з нерівності Коші-Буняковського
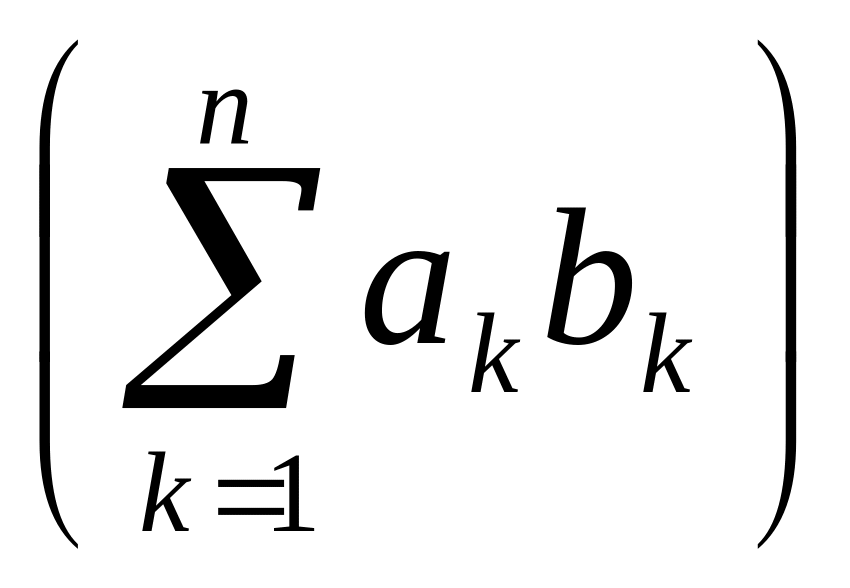
![]()
![]()
![]() .
Властивості 1-4 скалярного добутку
перевіряються безпосередньо.
.
Властивості 1-4 скалярного добутку
перевіряються безпосередньо.
Найпростіший ортогональний базис у утворюють вектори
е =(1,0,0,…),
е =(0,1,0,…), (5)
е![]() =(0,0,1,…),
=(0,0,1,…),
……………..
Ортогональність
і нормованість системи ясні, крім того
система (5) повна: нехай х=(х
,…,х
,…)
– будь-який вектор з
і х![]() =(х
,…,х
,0,0,…).
Тоді х
- лінійна комбінація векторів е
,…,
е
і при n
=(х
,…,х
,0,0,…).
Тоді х
- лінійна комбінація векторів е
,…,
е
і при n![]()
![]()
![]() 0.
0.
3. Простір С [a, b], що складається з неперервних дійсних функцій на [a, b], зі скалярним добутком – евклідів простір.
![]() (6)
(6)
Серед
різноманітних базисів, що існують в
ньому, можна вказати на тригонометричну
систему, що складається з функцій![]()
![]() ,
,
![]() ,
,
![]()
![]() .
(7)
.
(7)
Ортогональність системи перевіряється безпосередньо.
Якщо
розглядаються неперервні функції на
відрізку довжини 2![]() , наприклад [-
,
],
то відповідна тригонометрична система
буде:
, наприклад [-
,
],
то відповідна тригонометрична система
буде:
![]() ,cos(nt),
sin(nt)
(n=1,2,…).
,cos(nt),
sin(nt)
(n=1,2,…).
Система (7) повна, тобто кожна неперервна функція може бути представлена у вигляді лінійної комбінації даних функцій.
Доведемо, що система (7) є повною.
Згідно
з теоремою Вейєрштрасса всяка неперервна
функція
![]() на відрізку [a,
b],
яка приймає на кінцях відрізка однакові
значення, може бути представлена як
границя рівномірно збіжної послідовності
тригонометричних многочленів, тобто
лінійних комбінацій елементів системи
(7). Така послідовність і подавно збіжна
до
по нормі в просторі С
[a,
b].
Якщо ж функція f
- довільна функція в С
[a,
b],
то її можна подати, як границю (по нормі
простору С
[a,
b])
послідовності функції
на відрізку [a,
b],
яка приймає на кінцях відрізка однакові
значення, може бути представлена як
границя рівномірно збіжної послідовності
тригонометричних многочленів, тобто
лінійних комбінацій елементів системи
(7). Така послідовність і подавно збіжна
до
по нормі в просторі С
[a,
b].
Якщо ж функція f
- довільна функція в С
[a,
b],
то її можна подати, як границю (по нормі
простору С
[a,
b])
послідовності функції
![]() ,
кожна з яких співпадає з f
на відрізку [a,b-
,
кожна з яких співпадає з f
на відрізку [a,b-![]() ],
лінійна на [b-
,b]
і в точці b
приймає те значення, що і в a.
Звідси, кожен елемент в C
[a,b]можна
приблизити як завгодно точно (в метриці
цього простору) лінійними комбінаціями
елементів системи (7), а це і означає її
повноту.
],
лінійна на [b-
,b]
і в точці b
приймає те значення, що і в a.
Звідси, кожен елемент в C
[a,b]можна
приблизити як завгодно точно (в метриці
цього простору) лінійними комбінаціями
елементів системи (7), а це і означає її
повноту.
f(x)

![]()
![]()
![]()
