Границя функції
Приклад.
y=x2+1 Намалюємо графік функції. Функція визначена в деякому (навіть в будь-якому) проколотому околі точки x0 = 1.
Розглянемо
будь-яку послідовність точок xn
на
осі Ох із цього проколотого околу таку,
що наближається до точки 1: xn
1, n
,
.
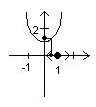
Побудуємо відповідну послідовність значень функції yn = ƒ(xn) - послідовність на осі Оу і знайдемо її границю:
y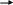
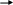n
2, n
.
Вона буде однаковою для будь-якої
початкової послідовності xn
.
В такому випадку число 2 називається
границею функції x2+1
в точці 1 і записують
y 2, x
1, або lim
(x2+1)
= 2.
x 1
П
ри
знаходженні границь допомагають графіки
функцій.
Приклади.
lim
= 1, lim
= 0, lim
= 0, lim
=
.
х
1 х +
х
х
0
О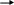
значення.
(за Гейне) Нехай ƒ(x)
визначена в деякому проколотому околі
точки x0.
А
називається
границею
функції в точці x0,
якщо для будь – якої послідовності xn
з цього проколотого околу, такої що xn
x0,
n
,
відповідна послідовність значень
функції yn
= ƒ(xn)
А, n
.
П
означається
ƒ(x)
А, x
x0
,
або
lim
ƒ(x)
= А.
x
x0
x 0 і А можуть бути числами або символами + ,- , .
П
риклад
функції, яка не має границі. y
= sin
x,
визначена при всіх х є
,
тому
можна розглядати її границю і при x0= + .
Для
послідовності {nП}
+
,
sin
(nП)=0
0,n
+
,
а
для послідовності {
+
2nП}
+
,
sin(
+
2nП)=1
1,n
+
,
, тому границі
нема.
Отже, границя функції в точці або на нескінченності може бути числом, нескінченністю, або взагалі не існувати.
П
риклад.
y
= 2x
+ 1, x0
= 2.
5+
5
5-
2-
2
2+
.
Якщо взяти будь-який окіл точки 5 на
осі Оу (5-
,
5+
),
то можна побудувати такий окіл точки 2
на осі Ох (2-
,
2+
),
що всі точки околу на осі Ох переходять
при відображенні нашою функцією в
початково вибраний окіл на осі Оу.
|
1 |
0,5 |
|
δ |
0,5 |
0,25 |
/2 |
Означення. (за Коші) Нехай ƒ - визначена в деякому проколотому околі точки x0. А називається границею функції ƒ в точці x0, якщо для будь-якого
-околу точки А (на осі Оу) існує такий проколотий δ-окіл точки x0 (на осі Ох), що при відображенні функцією попадає в -окіл точки А.
Теорема. Означення за Гейне і за Коші еквівалентні.
Означення. Якщо в означенні за Гейне або за Коші замість проколотого околу брати тільки лівий окіл точки x0, то А називають лівою границею функції ƒ в точці x0 і позначається
lim
ƒ(x)
= А,
або ƒ(x)
А, x
x0-
або ƒ(x0-
)=А.
x
x0-
Аналогічно для правої границі розглядатимемо правий окіл (x0; x0+ δ)
lim
ƒ(x)
= А,
або ƒ(x)
А, x
x0+
або ƒ(x0+
)=А.
x
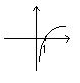
x0+
Приклад.
у= ln x lim ln x = - ,
x
0+
ƒ(0+) = -
Тут ліву границю шукати не можна, бо функція невизначена зліва від точки 0.
П
риклад.
f(x)={
2
1
1
тому
не
існує.
Теорема. Границя функції в точці x0 існує тоді і тільки тоді, коли права і ліва границі існують і однакові.
Означення. Функція ƒ називається нескінченно великою в точці x0, якщо її границя в цій точці є нескінченністю.
Функція ƒ називається нескінченно малою в точці x0, якщо її границя в цій точці дорівнює 0.
Приклади.
- нескінченно мала на + і на ;
- нескінченно велика в точці 0;
sin x - нескінченно мала в точці 0;
ln x - нескінченно велика в точці 0.
- не є ні нескінченно малою ні нескінченно великою в точці 1.