3. Графическое представление выборочных функций.

По данным таблицы частот строят гистограмму:

_{Строят график полигона распределения} пробега автомобилей_:

4. Построение функции распределения

Для построения эмпирической функции распределения небходимо создать исходную таблицу (таблица 6). В первом столбце указываются границы интервалов, а во втором соответствующие им накопленные вероятности. Исходная таблица данных отличается от таблицы частот тем, что границы интервалов повторяются, так как значение верхней границы интервала равно значению нижней границы следующего интервала.

Границы интервалов	Накопленная вероятность
516,5	2
525,5	2
525,5	9
534,5	9
534,5	14
543,5	14
543,5	22
552,5	22
552,5	42
561,5	42
561,5	61
570,5	61
570,5	82
579,5	82
579,5	94
588,5	94
588,5	106
597,5	106
597,5	109
606,5	109
606,5	110
615,5	110

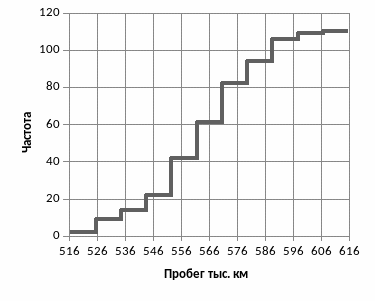
График эмпирической функции распределения

пробега

автомобилей до снятия с эксплуатации.

Таблица 6.

5. Вывод:

_По данным гистограммы и графику _{полигона распределения пробега автомобилей можно сделать вывод, что наибольшая частота наблюдаеться у автомобилей с пробегом 547,5 и 565,5 тыс. км. Это сведетельствует о том, что автомобили с пробегом в этих числовых значениях чаще всего, а именно 20 из 25 автомобилей, подлежат снятию с эксплуатации. Наименьшее число автомобилей, подлежащих снятию с эксплуатации наблюдаеться с пробегом 610,5 тыс. км. – 1 автомобиль из 25.}

По графику эмпирической функции распределения пробега можно сделать вывод:

Вероятность снятия с эксплуатации автомобилей с пробегом до 520 тыс. км будет минимальной: 1,8 % (2 автомобиля из 111)

С пробегом более 605 тыс. км будет максимальной: 99% (110 автомобилей из 111)

6