13. Свойства периодических кривых.

Несинусоидальные периодические кривые, с которыми прихо­дится встречаться в электротехнике, являются симметричными относительно оси абсцисс или ординат или начала координат.

Так как среднее за период Т значение синусоиды равно нулю (§ 10.3), то среднее за период значение несинусоидальных коле­баний, состоящих из нескольких синусоид и не содержащих по­стоянной составляющей, также равно нулю.

Или иначе, если у несинусоидальной периодической кривой среднее за период значение (ордината) равна нулю, то постоянная составля­ющая такой кривой также равна нулю. Среднее значение периодиче­ской кривой, состоящей из постоянной составляющей и ряда гармо­ник, равно постоянной составляющей.

Так, например, пульсирующая кривая (рис. 18.2в) мгновенной мощности Р в цепи переменного тока с активным сопротивлени­ем может быть разложена на постоянную составляющую и сину­соиду (гармонику), изменяющуюся с двойной частотой (см. выра­жение (11.3)), т.е. вторую гармонику. Среднее значение такой кривой равно постоянной составляющей, т. е. активной мощно­сти Р=Ш(см. (11.4)).

Периодическая кривая называется симметричной относитель­но оси абсцисс, если на расстоянии половины периода они имеют ординаты, одинаковые по величине, но обратные по знаку (рис. 18.2а), т.е. отрицательная полуволна такой кривой пред­ставляет собой зеркальное изображение положительной полу­волны.

Кривые, симметричные относительно оси абсцисс, не содержат постоянной составляющей и четных гармоник (рис. 18.1). Такая кривая содержит только нечетные гармоники:

К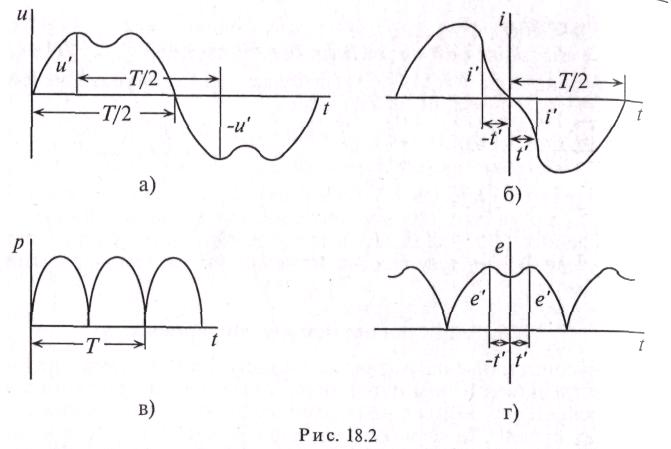 ривые, симметричные относительно оси абсцисс, встречаются в электротехнике часто, например кривые тока в катушке со ста­льным сердечником, подключенной к сети с синусоидальным на­пряжением.

Периодическая кривая называется симметричной относительно начала координат, если любым двум абсциссам, имеющим одина­ковое значение, но разные знаки, соответствуют ординаты, рав­ные по величине и обратные по знаку (рис. 18.26).

Кривые, симметричные относительно начала координат, не со­держат постоянной составляющей и косинусоид. Такая кривая содержит только синусоиды:

Часто встречаются кривые, симметричные относительно оси абсцисс и начала координат

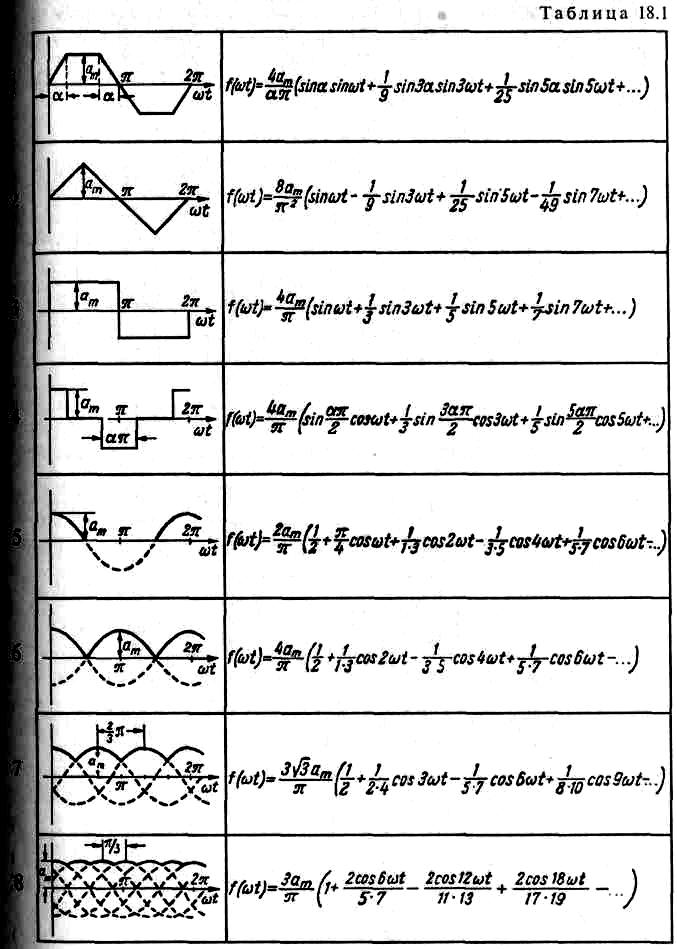
(кривые 1, 2, 3 и 4 таблицы 18.1). Та­кие кривые не содержат постоянной составляющей, четных гармоник и косинусоидальных составляющих, а содержат только не­четные синусоиды:

Кривая, симметричная относительно оси ординат, изображена на рис. 18.2г. Такая кривая не содержит синусоид. Она содержит постоянную составляющую и косинусоиды:

В таблице приведены несинусоидальные периодические кривые геометрически правильной формы и разложение их в ряд Фурье.

14. Несинусоидальный ток в линейных электрических цепях.

15. Действующее значение несинусоидальной величины.

Действующим называют значение несинусоидального тока, эк­вивалентное постоянному току по тепловому действию.

При этом нужно учесть, что несинусоидальный ток складывает­ся из постоянной составляющей и ряда гармоник:

Каждая составляющая несинусоидального тока выделяет тепло в некотором элементе цепи с сопротивлением R. Воспользовав­шись рассуждениями § 10.3 для определения действующих значе­ний тока гармоник и постоянной составляющей несинусоидаль­ного тока, можно сделать вывод, что

(18.19)

г де /₀ — постоянная составляющая несинусоидального тока; I₁, I₂, I_k, — действующее значение токов гармоник, т.е.

Таким образом, действующее значение несинусоидального тока является средней квадратичной величиной постоянной состав­ляющей и действующих значений токов гармоник.

С учетом выражения (10.9) действующее значение несинусоида­льного тока можно определить по формуле

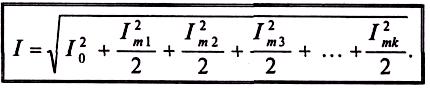(18.20)

Аналогично действующее значение несинусоидального напря­жения определяется выражением

(18.21)

Действующее значение несинусоидального напряжения является средней квадратичной величиной постоянной составляющей и дей­ствующих значений напряжений гармоник.

Действующие значения несинусоидальных токов и напряжении измеряются амперметрами и вольтметрами электромагнитной, электродинамической и тепловой систем.

Кроме коэффициента формы К_ф и коэффициента амплитуды K_а, определение которых дано в §10.3 (выражение (10.10) и (10.11)), несинусоидальные периодические кривые характеризу­ются коэффициентом искажений К_И. Коэффициент искажений определяется отношением действующего значения основной (первой) гармоники тока или напряжения к действующему значению этих не­синусоидальных величин. Такое определение аналогично д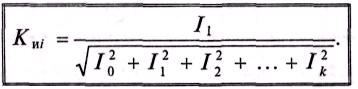 ля ЭДС, магнитного потока и т. д. Г Коэффициент искажения тока

К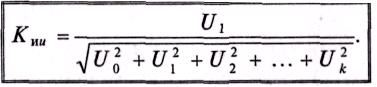 оэффициент искажения напряжения

(18.23)

Для синусоиды К_И=1.

Чем меньше коэффициент искажения отличается от единицы, тем ближе к синусоиде данная кривая.

Так, например, для треугольной формы кривой (кривая 2 таб­лицы 18.1) - К_и≈0,99, а для прямоугольной формы кривой (кри­вая 3 таблицы 18.1) - К_И≈0,9.

( В электронике и радиотехнике несинусоидальность кривой ха­рактеризуют коэффициентом гармоник, показывающим удельный вес высших гармоник К_r относительно первой (основной) гармоники:

(

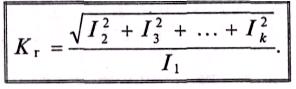Чем меньше коэффициент гармоник, тем ближе к синусоиде Несинусоидальная кривая.