11. Основные понятия несинусоидального тока. Несинусоидальный ток Основные понятия

Периодическими несинусоидальными токами называют токи, изменяющиеся во времени по периодическому несинусоидаль­ному закону.

Несинусоидальные токи возникают при различных режимах ра­боты электрических цепей. Таких режимов четыре.

1. Источник электрической энергии вырабатывает несинусо­идальную ЭДС или несинусоидальный ток, а все элементы цепи (активные сопротивления, индуктивности и емкости) ли­нейны, т. е. от величины тока не зависят. Такая цепь называется линейной.

2. Источник электрической энергии вырабатывает синусоида­льную ЭДС, но один или несколько элементов цепи нелинейны, т.е. имеют нелинейные характеристики (катушка со стальным сердечником, выпрямители).

3. Источник электрической энергии вырабатывает несинусо­идальную ЭДС, а в электрическую цепь входят одно или несколь­ко нелинейных сопротивлений.

4. Источник электрической энергии вырабатывает постоянную или синусоидальную ЭДС, а один или несколько элементов цепи в процессе работы изменяют свои параметры.

Таким образом, причиной несинусоидальности в электриче­ской цепи может быть источник электрической энергии или по­требитель, т. е. нагрузка, или оба одновременно.

В электрических генераторах (источниках электрической энер­гии) основной причиной несинусоидальной ЭДС (напряжений) является неравномерное распределение магнитного потока (по окружности) в зазоре между статором и ротором генератора.

Причиной появления несинусоидальных токов в нагрузке явля­ется, как указывалось выше, нелинейные вольт-амперные харак­теристики потребителей или преобразователей, например транс­форматоров. В настоящей главе рассмотрен расчет и особенно­сти работы линейных электрических цепей при воздействии на них несинусоидальных ЭДС, т. е. первый из перечисленных вы­ше режимов работы. Остальные режимы рассматриваются в гла­ве 19 и в специальной технической и справочной литературе.

12. Основные понятия о гармониках. Гармоники

Несинусоидальные колебания могут быть периодическими и непериодическими. При рассмотрении периодических несину­соидальных колебаний можно воспользоваться теоремой Фурье, согласно которой любая периодически изменяющаяся величи­на может быть представлена в виде суммы постоянной состав­ляющей и ряда синусоидальных составляющих с кратными часто­тами.

Синусоидальные составляющие несинусоидальных колебаний назы­ваются гармониками.

Синусоидальная составляющая, частота которой равна частоте несинусоидальной периодической величины, называется основ­ной, или первой, гармоникой. А синусоидальные составляющие, частоты которых в 2, 3, ..., А; раз больше частоты несинусоидаль­ной величины, называются соответственно 2-й, 3-й, ..., k-й гар­моникой.

Аналитическое выражение несинусоидальной периодической функции можно записать так:

(18.1)

г де— несинусоидальная величина, изменяющаяся с частотой

• - постоянная составляющая несинусоидальной величины;

- амплитуды соответственно 1-й, 2-й, 3-й и к-й гармоник, т. е. синусоидальных составляющих с частотой - начальные фазы соответственно 1-й, 2-й, I 3-й и к-й гармоник.

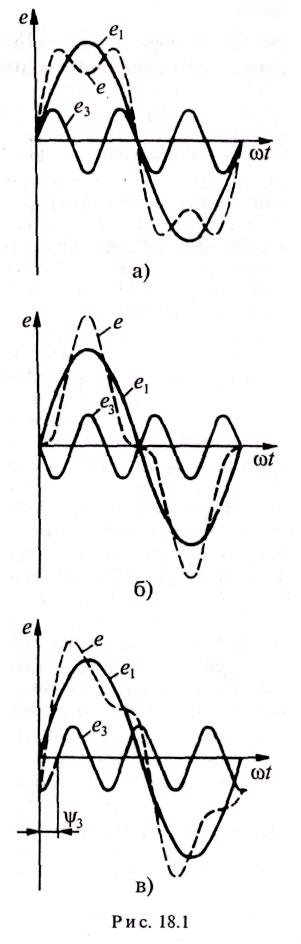
Из выражения (18.1) следует, что сложение синусоидальных колебаний (гармоник) с различными частотами и разными нача­льными фазами дает несинусоидальное колебание. Убедиться в этом можно при графическом сложении двух синусоидальных ЭДС е_х и е₃ (рис. 18.1). На рис. 18.1а складываются две синусоиды где

На рис. 18.16 складываются две синусоиды , где

На рис. 18.1в складываются две синусоиды , где

Как видно, суммарные колебания (e = e₁ + e₃) в рассмотренных трех случаях (а, бив) получились различными.

И з рис. 18.1 также видно, что не все несинусоидальные перио­дические колебания раскладыва­ются в полный ряд Фурье. В дан­ном случае складываются только 1-я и 3-я гармоники, и результи­рующие колебания могут быть записаны в виде:

Таким образом, несинусоидаль­ные кривые е, изображенные на рис. 18.1, раскладываются в ряд Фурье только на нечетные гармоники 1-ю и 3-ю, т.е. в раз­ложении отсутствуют постоянная составляющая, все четные гармо­ники и высшие н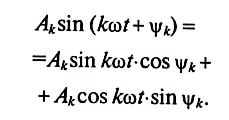 ечетные гармо­ники (5-я, 7-я, 9-я и т.д.).

Гармоники можно преобразо­вать, применив из тригономет­рии формулу синуса суммы двух углов. Из выражения (18.1) к-ю гармонику можно представить в виде

О бозначив постоянные величины выражения (18.2)

можно получить

(18.4)

Тогда выражение (18.1), т.е. ряд Фурье для несинусоидальной периодической функции, примет вид

(18.5)

В отличие от амплитуды к-й гармоники А_к, постоянные величи­ны В_к и С_к могут быть положительными или отрицательными.

Такая запись (18.5) характерна тем, что гармоники составляют ряд синусов и ряд косинусов с начальными фазами, равными нулю