10. Зарядка, разрядка и саморазрядка конденсаторов.

Зарядка, разрядка и саморазрядка конденсатора

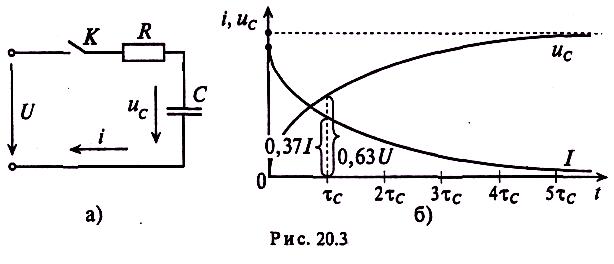
Если конденсатор с сопротивлением (утечки) R и емкостью С подключить к источнику с постоянным напряжением U(замыканием ключа К), то в цепи (рис. 20.3а) появится ток зарядки конденсатора (см. (11.16)):

(20.12)

е u_с - напряжение на конденсаторе в любой момент времени переходного процесса.

По второму закону Кирхгофа для цепи зарядки конденсатора (рис. 20.3а) можно записать уравнение (20.13)

г де произведение RC имеет размерность времени, обозначается левой τ и называется постоянной времени переходного процесса RС-цепи, т. е.

. (20.14)

> Уравнение (20.13) можно записать в виде (20.15)

Если в уравнении (20.15) разделить переменные, проинтегриро­вать, а затем спотенцировать, то получится выражение

(20.16)

г де U - установившееся напряжение u_y RС-цепи; свободная составляющая напряжения и_св на конденсаторе;т. е.

и_с=и_у + и_св.

Следовательно, напряжение на заряжающемся конденсаторе в любой момент времени / переходного процесса определяется вы­ражением

(20.17)

По (20.17), пользуясь Приложением 9, можно определить, что за время t=τ_c конденсатор зарядится до напряжения и_с= 0,63U, а за время t=4,6τ_c - до напряжения и_с= 0,99U.

Теоретически зарядка конденсатора длится бесконечно долго, а практически конденсатор считается заряженным, когда напря­жение на нем достигает 99 % напряжения источника U.

Таким образом, и в RC-цепи, чем больше постоянная време­ни τ_с, тем больше времени t тратится на зарядку конденсатора, т. е. и в данном случае постоянная времени τ_с характеризует дли­тельность зарядки и разрядки конденсатора.

Т ок i при зарядке конденсатора (см. (20.13)) уменьшается по за­кону

(20.18)

г де- максимальный ток, который имеет место в начальный момент е=0 зарядки конденсатора (момент коммутации).

За время t = τ_с ток в цепи заряжающегося конденсатора уменьшится до 0,37 I, а за время t=4,6τ_с - до 0,01 I, при котором пере­ходный процесс можно считать законченным.

Графики изменения напряжения на конденсаторе и тока в цепи зарядки конденсатора изображены на рис. 20.36.

Е сли конденсатор емкостью С, заряженный предварительно до напряжения U, разряжать через резистор с сопротивлением R (рис. 20.4а), то напряжение и_с на конденсаторе и ток в цепи разрядки будут уменьшаться по закону

(20.19) (20.20)

г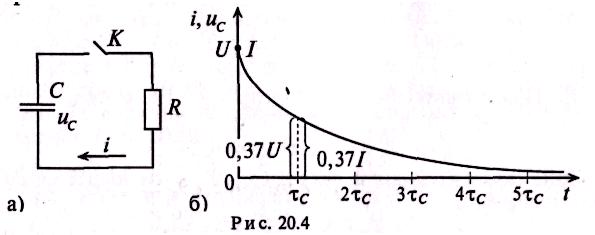 де U — напряжение на конденсаторе до начала разрядки (при t = 0), а — максимальный ток в начальный момент разрядки (при t=0), τ_с=RС— постоянная времени в цепи разрядки конденсатора.

За время t=τ_C напряжение и ток уменьшатся до 37 % своих максимальных значений. Изменение напряжения и тока на разряжающемся конденсаторе показаны на рис. 20.46 (в разных масштабах).

Если конденсатор емкостью С, заряженный до напряжения U, отсоединить от источника, то он будет разряжаться через свой диэлектрик. Напряжение на нем будет уменьшаться по закону

Процесс разрядки конденсатора через свой диэлектрик называется саморазрядом.

Постоянная времени саморазряда зависит от физических свойств диэлектрика

(20.21) где ρ — удельное сопротивление диэлектрика; ε₀ — электрическая постоянная; ε_г — диэлектрическая проницаемость диэлектрика (относительная).

Для определения напряжения, тока, ЭДС в любой момент пе­реходного процесса RL-цепи и RС-цепи можно воспользоваться таблицей показательных функций (Приложение 9).