8. Подключение катушки индуктивности к источнику с постоянным напряжением.

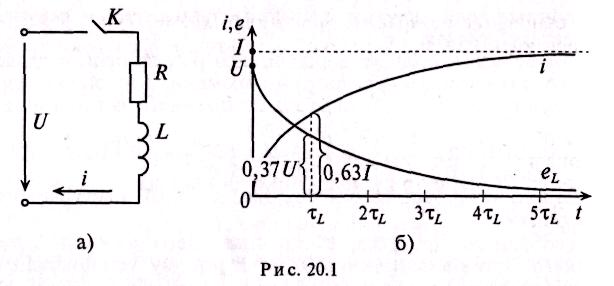
Если катушку индуктивности (RL) подключить к источнику с постоянным напряжением U (замыкание ключа К), то ток i в неразветвленной цепи (рис. 20.1а) будет увеличиваться от нуля (в начале переходного процесса) до установившегося значения

(20.3)

Установившийся, т. е. постоянный, ток I не индуктирует в ка­тушке ЭДС самоиндукции, поэтому индуктивное сопротивление в установившемся режиме при условии (20.3) отсутствует.

Этот увеличивающийся ток i индуктирует в индуктивности L катушки ЭДС самоиндукции (см. (9.11))

Следовательно, для любого момента времени переходного про­цесса по второму закону Кирхгофа можно записать

(20.4)

Разделив уравнение (20.4) на R, получают

(20.5)

В уравнении (20.5)— установившийся в конце переходного процесса ток (i_у).

Отношение имеет размерность времени обозначается буквой τ (тау) и называется постоянной времени RL-цепи, т. е.

(20.6)

Тогда уравнение (20.5) можно записать в виде

(20.7)

Если это уравнение проинтегрировать, предварительно разде­лив переменные (ток и время), а затем спотенцировать, то полу­чим выражение

(20.8)

где е - основание натурального логарифма (е = 2,71); I - устано­вившийся ток (i_у); - свободный ток (i_св), так как i= i_у+ i_св,

Таким образом, уравнение, которое позволяет определить величину тока в цепи с индуктивностью L в любой момент переходного процесса RL-цепи при подключении реальной катушки индуктивности к источнику с постоянным напряжением U, записыва­ется в виде

(20.10)

Воспользовавшись Приложением 9, по выражению (20.10) можно определить, что за время t=τ_L ток в цепи увеличивается до 0,63I, а за время /= 4,6τ_L - до 0,99I, т. е. до 99 % установившегося тока I.

Теоретически переходный процесс происходит бесконечно долго. Практически переходный процесс в рассматриваемой цепи cчитается законченным, когда ток I увеличивается до 99 % устаyовившегося тока I.

Как видим, чем больше τ_L, тем больше времени t длится переходный процесс.

Таким образом, постоянная времени τ_L определяет скорость переходного процесса или его длительность.

I ЭДС самоиндукции в рассматриваемой цепи, вызванная свободным током i_св, определяется выражением

(20.11)

Таким образом, ЭДС самоиндукции в RL-цепи, подключенной к источнику с постоянным напряжением U, будет уменьшаться. Так, за время t=τ_L, ЭДС самоиндукции согласно (20.11) уменьшится до 0,37 U, а за время t= 4,6τ_L - до 0,01 U, т. е. до 1 % постоянного напряжения U.

Увеличение тока и уменьшение ЭДС самоиндукции катушки при подключении катушки к источнику с постоянным напряже­нием U показаны на графике рис. 20.16.

9. Отключение и замыкание rl-цепи.

Если цепь с катушкой, в которой проходит установившийся ток I (рис. 20.1а), разомкнуть, то ток i в такой цепи с большой скоростью уменьшается до нуля и в катушке индуктируется большая ЭДС самоиндукции e_L

Эта ЭДС полностью приложена к клеммам ключа, так как при размыкании сопротивление ключа становится бесконечно большим. Эта ЭДС вызывает значительное увеличение электрического поля между контактами ключа, а следовательно, и напряженности поля. Большая напряженность электрического поля может вызвать искровой и даже дуговой разряд между размыкающимися контактами ключа, в результате чего обгорают контакты ключа.

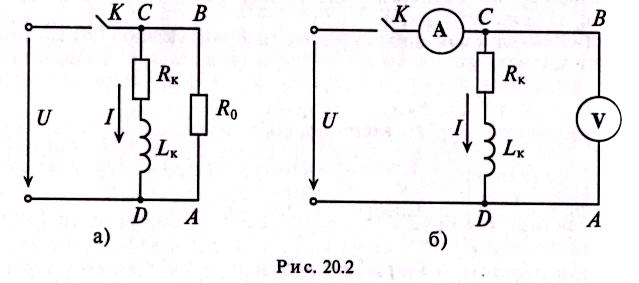
Поэтому рубильники в RL-цепях шунтируются специальны­ми устройствами, которые обеспечивают гашение дугового раз­ряда. Для гашения дугового разряда необходимо одновременно с отключением катушки индуктивности от источника замкнуть ее на разрядное сопротивление Ro (рис. 20.2а).

Уменьшение тока i_св при отключении катушки от источника (рис. 20.1а) происходит по закону

Наглядно это уменьшение можно наблюдать на рис. 20.16, если кривую изменения e_L считать кривой уменьшения тока i_св в соот­ветствующем масштабе.

П остоянная времени при отключении катушки от источника с постоянным напряжением U определяется как и при включе­нии катушки на это напряжение, т. е.

Если катушку с установившимся током I, зашунтированную сопротивлением R₀, (рис. 20.2а), отключить от источника (разомкнуть ключ К), то в замкнутом контуре ABCD в начальный момент коммутации (t_o = O) пройдет ток т.е. установившийся ток. Этот ток I может оказаться недопустимо большим ря резистора с сопротивлением Ro.

Для определения активного сопротивления катушки R_K и пол­ого ее сопротивления Z_k включают амперметр А и вольтметр V (рис. 20.26), т.е. вместо резистора с сопротивлением Ro в контур АBCD (рис. 20.26) включен вольтметр V. Этот вольтметр может не быть рассчитан на установившийся ток I, проходящий через него при размыкании ключа, в результате чего может сгореть. Чтобы не «сжечь» вольтметр (рис. 20.26), сначала необходимо отключить вольтметр, а затем разомкнуть ключ К.

Как видно, за счет переходных процессов в цепях с индуктивностью возникают большие токи и напряжения. С этим необходимо считаться и учитывать при проектировании и эксплуатации епей с индуктивностью.