11

Title

Зміст

Завдання 3

Теоретичні відомості 4

Схема то опис роботи приладу 7

Результат роботи приладу 8

Висновки 10

Використана література 11

Завдання

Побудуйте пристрій, який би виконував операцію R=(Е-В)*2.

Теоретичні відомості

Напівсуматор - це вузол (рис.1,а,б) з двома входами та двома виходами, який виконує операцію арифметичного додавання двох однорозрядних чисел A та B у відповідності до наступного правила: при будь-яких наборах сигналу A та B на виході сигналу суми S' формується результат додавання по модулю два, на виході сигналу переносу P' у всіх випадках буде 0, крім A=B=1, тоді P'=1. Таким чином, для реалізації напівсуматора необхідні суматор по модулю два та логічний елемент І.

  

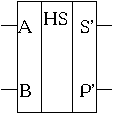
а)

б)

Рисунок 1 Напівсуматори: а) функціональна схема, б) умовне позначення;

Повний однорозрядний суматор виконує операцію арифметичного додавання двох однорозрядних чисел Ai та Bi з урахуванням переносу з молодшого розряду. Він має три входи і два виходи (суми S та сигналу переносу P). Правила роботи суматора визначає таблиця 16.

Таблиця 1 Правила роботи повного однорозрядного суматора

Входи			Виходи		Входи				Виходи
Ai	Bi	Pi-1	Si	Pi		Ai	Bi	Pi-1	Si	Pi
0	0	0	0	0		1	0	0	1	0
0	0	1	1	0		1	0	1	0	1
0	1	0	1	0		1	1	0	0	1
0	1	1	0	1		1	1	1	1	1

Багаторозрядні суматори виконують операцію арифметичного додавання двох багаторозрядних чисел. Кількість входів та виходів суматора визначається розрядністю доданків. За організацією переносу розрізняють суматори з послідовним (рис.17) та паралельним перенесенням. За першим способом побудовані, наприклад, чотирьохрозрядні суматори К155ИМ3, К555ИМ7. Швидкодія такого суматора визначається часом розповсюдження сигналу через усі його елементи, і тому вона значно нижча за швидкодію елементів.

Суматори з паралельним перенесенням володіють найвищою швидкодією завдяки тому, що мають в своїй структурі схему прискореного перенесення (СПП) в усі розряди одночасно. Прикладом такого суматора є ІМС К555ИМ6. Багато ІМС чотирьохрозрядних суматорів мають вмонтовану СПП, наприклад, К561ИМ1, 564ИМ1 (рис.3,а). В цих суматорів затримка формування суми більша за затримку формування сигналу групового переносу: наприклад, у 564ИМ1 затримка по виходах S4 та P складає 1.1 та 0.14мкс відповідно. Тому вмонтована СПП дозволяє значно прискорити процес додавання багаторозрядних чисел в пристрої сумування, який створений шляхом з'єднання декількох ІМС суматорів.

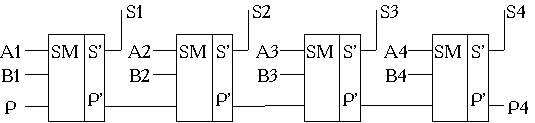
Рисунок 2 Cуматор з послідовним перенесенням

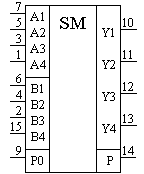
Рисунок 18 Суматор 564ИМ1

Доповня́льний код — найпоширеніший спосіб представлення від'ємних чисел у комп’ютерах. Дозволяє замість команди віднімання використовувати команду додавання , для знакових і беззнакових чисел, що зменшує вимоги до архітектури комп’ютера. Доповняльний код від’ємного числа можна отримати так: інвертувати модуль числа у двійковому вигляді («перше доповнення») і додати одиницю («друге доповнення») або відняти від число від нуля. Математично доповняльний код X_доп = 2^N+1 - X, де X — число, яке треба представити у доповняльному коді, N — к-сть розрядів числа.

Найстарший біт
0	1	1	1	1	1	1	1	=	127
0	1	1	1	1	1	1	0	=	126
0	0	0	0	0	0	1	0	=	2
0	0	0	0	0	0	0	1	=	1
0	0	0	0	0	0	0	0	=	0
1	1	1	1	1	1	1	1	=	−1
1	1	1	1	1	1	1	0	=	−2
1	0	0	0	0	0	0	1	=	−127
1	0	0	0	0	0	0	0	=	−128

Восьмирозрядні доповняльні коди

Переваги

• Комірка пам'яті може містити як n-бітні додатні числа, так і (n−1)-бітні числа зі знаком, причому операції додавання, віднімання і зсуву вліво однакові для обох форматів.

• Відсутність числа «-0». У коді доповнення до 1 таке число є.

Недоліки

• Стосовно складних форматів (таких, як плаваюча кома або двійково-десятковий код) переваги втрачаються.

• Модуль найбільшого числа не дорівнює модулю найменшого. Наприклад, для знакової цілої 8-байтової змінної найбільше число це 127₁₀ = 7F₁₆ = 01111111₂, а найменше: -128₁₀ = 80_{16,доп. код} = 10000000_{2,доп. код}. Відповідно, не для кожного числа можна записати протилежне. Операція зміни знаку може вимагати додаткової перевірки.

Схема то опис роботи приладу

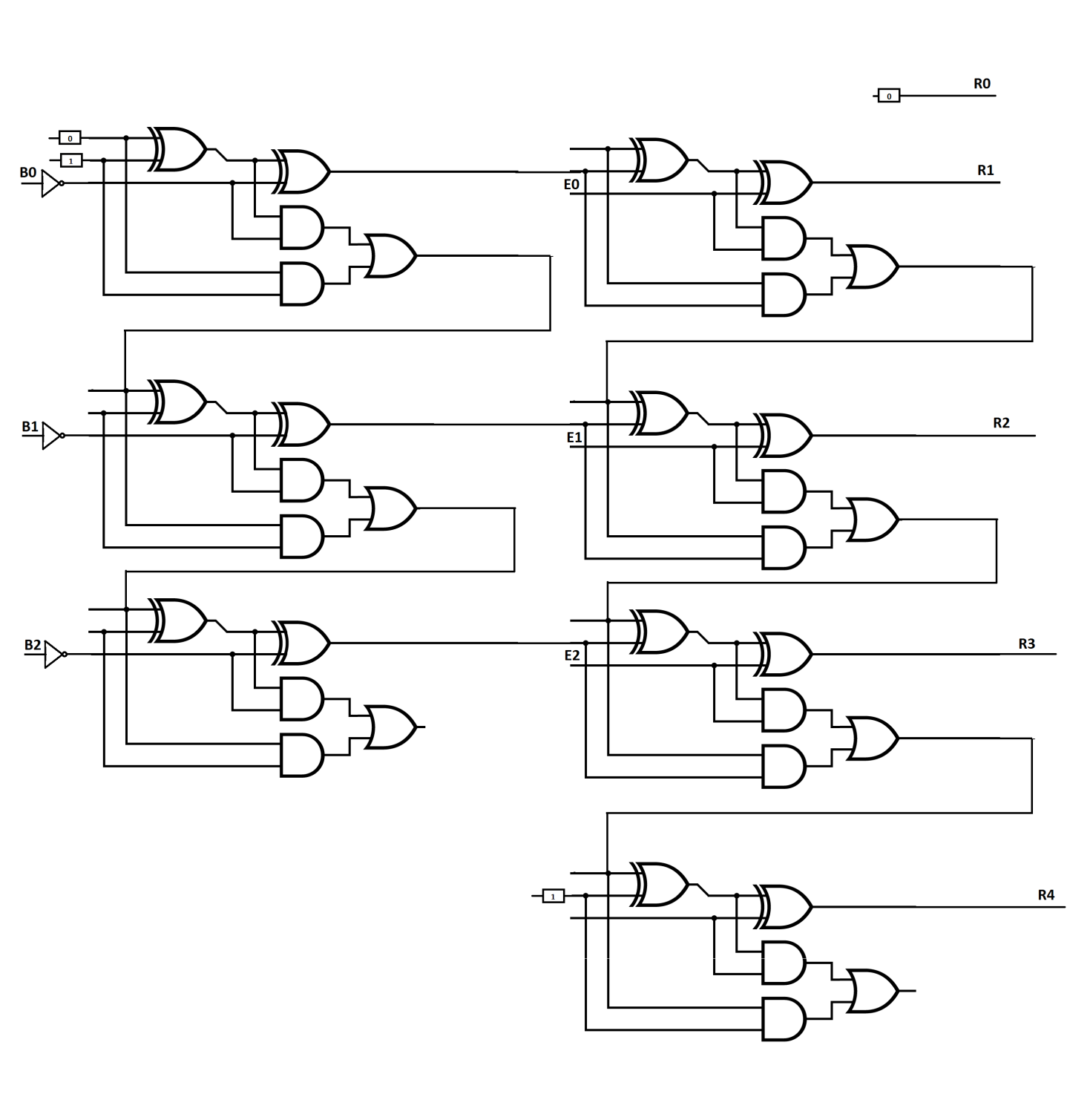Організовані два трибітні сумматори, З адопомогою інверторів, першого сумматора, то жорсткої «1» на 3-му вході 2-го суматора число (-1)*В переводиться у форму доповню вального коду. На виході другого суматора отримуємо Е-В. Множення на 2 виконується за допомогою додатково введеного молодшого біта з жорстко заданим «0».

Результат роботи приладу

E	B	R
0	0	0
0	1	14
0	2	12
0	3	10
0	4	8
0	5	6
0	6	4
0	7	2
1	0	2
1	1	0
1	2	14
1	3	12
1	4	10
1	5	8
1	6	6
1	7	4
2	0	4
2	1	2
2	2	0
2	3	14
2	4	12
2	5	10
2	6	8
2	7	6
3	0	6
3	1	4
3	2	2
3	3	0
3	4	14
3	5	12
3	6	10
3	7	8
4	0	8
4	1	6
4	2	4
4	3	2
4	4	0
4	5	14
4	6	12
4	7	10
5	0	10
5	1	8
5	2	6
5	3	4
5	4	2
5	5	0
5	6	14
5	7	12
6	0	12
6	1	10
6	2	8
6	3	6
6	4	4
6	5	2
6	6	0
6	7	14
7	0	14
7	1	12
7	2	10
7	3	8
7	4	6
7	5	4
7	6	2
7	7	0

Висновки

Під час виконання роботи була сконструйована схема для виконання операції (Е-В)*2 над трьохбітними числами, використаний доповню вальний метод. Схема працює як і передбачалося теорією. За умови B>E (по причині використаного методу віднімання і представлення результатів) йде переповнення,яке ми спостерігали у таблиці результатів. Видно, всі операції проводяться для трьохбітних чисел (власне (Е-В) при умові (E-B)<0 можна отримати, якщо від результату відняти 8). Поставлене завдання виконане.

Використана література

1. Погорілий С.Д. Програмне конструювання: Підручник / За ред. О.В. Третяка. – 2-е вид. – К.: Видавничо-поліграфічний центр «Київський університет», 2005.

2. Левитський С. М. Основи радіоелектроніки: Підручник. – К.: Видавничо-поліграфічний центр «Київський університет», 2007.