Билет № 05

1. Кинематический закон движения. Путь. Перемещение. Скорость. Ускорение. Физический смысл производной и интеграла.

Кинематические законы движения - это законы, отражающие зависимость кинематических величин - пути, скорости, ускорения от времени.

Путь в физике — длина участка траектории материальной точки.

Перемещение определяется как неправленый отрезок прямой, проведенный из начального положения движущейся точки в ее конечное положение. (векторная, метр)

Скорость определяется как векторная физическая величина, характеризующая быстроту перемещения тела.

Ускорение - векторная величина, характеризующая быстроту изменения скорости точки по её численному значению и по направлению.

Физический смысл производной. Если точка движется вдоль оси х и ее координата изменяется по закону x(t), то мгновенная скорость точки:

2. Закон изменения и сохранения момента импульса. Уравнение движения для вращения тела.

Закон сохранения момента импульса: момент импульса замкнутой системы сохраняется, т. е. не изменяется с течением времени. Закон сохранения момента импульса также как и закон сохранения энергии является фундаментальным законом природы. Он связан со свойством симметрии пространства - его изотропностью, т. е. с инвариантностью физических законов относительно выбора направления осей координат системы отсчета (относительно поворота замкнутой системы в пространстве на любой угол).

Изменение момента импульса связано с действием на тело внешних сил, а именно, с наличием момента силы. Если же момент внешних сил равен нулю, что справедливо, например, для центрального поля, то момент импульса тела остается постоянным. В этих условиях действует закон площадей – один из законов Кеплера, согласно которому при вращении тела радиус-вектор за равные промежутки времени «заметает» равные площади. Другими словами, по мере сближения с центром скорость вращения возрастает, а при удалении от него – уменьшается.

Закон вращательного движения тела выражается уравнением φ = f (t).

3. Термодинамические потенциалы. Энтальпия, свободная энергия.

Потенциалы термодинамические - определённые функции объёма (V), давления (р), температуры (Т), энтропии (S), числа частиц системы (N)и др. макроскопических параметров (x_i), характеризующих состояние термодинамической системы.

Энтальпия - потенциал термодинамический, характеризующий состояние термодинамической системы при выборе в качестве основных независимых переменных энтропии S и давления р. Обозначается H (S, р, N, x_l), где N — число частиц системы, x_i — другие макроскопические параметры системы. Э. — аддитивная функция, т. е. Э. всей системы равна сумме Э. составляющих её частей; с внутренней энергией U системы Э. связана соотношением

H = U + pV,

где V — объём системы. Полный дифференциал Э. (при неизменных N и x_i)имеет вид:

dH = TdS + Vdp.

Свобо́дная эне́ргия Гельмго́льца (или просто свобо́дная эне́ргия) — термодинамический потенциал, убыль которого в квазистатическом изотермическом процессе равна работе, совершённой системой над внешними телами.

Свободная энергия Гельмгольца для системы с постоянным числом частиц определяется так:

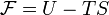• , где U — внутренняя энергия, T — абсолютная температура, S — энтропия.

Отсюда дифференциал свободной энергии равен:

• .

Видно, что это выражение является полным дифференциалом относительно независимых переменных T и V. Поэтому часто свободную энергию Гельмгольца для равновесного состояния выражают как функцию .

Билет № 09