Математично-статистичні

МІНІСТЕРСТВО ІНФРАСТРУКТУРИ УКРАЇНИ ДЕРЖАВНИЙ ЕКОНОМІКО-ТЕХНОЛОГІЧНИЙ УНІВЕРСИТЕТ ТРАНСПОРТУ Кафедра ТТА

Розрахункова робота

з дисципліни «МАТЕМАТИЧНО-СТАТИСТИЧНІ МЕТОДИ ДОСЛІДЖЕННЯ»

Виконала студентка групи 1-АТЗ-маг. Гуп'як Ю. В. Перевірила Кокряцька Н.І.

Київ 2011

ПЕРВИННИЙ СТАТИСТИЧНИЙ АНАЛІЗ

Таблиця 1. Результати вимірювання потенціометра, В.

1 84,3368 2 84,3403 3 84,3323 4 84,3371 5 84,3285 6 84,3385 7 84,3461 8 84,3417 9 84,3397 10 84,3515 11 84,3335 12 84,3371 13 84,324 14 84,3365 15 84,3413 16 84,3379 17 84,329 18 84,3463 19 84,3392 20 84,3414 21 84,3383 22 84,3419 23 84,3296 24 84,3381 25 84,3442 26 84,3354 27 84,3367 28 84,3435 29 84,3385 30 84,3348 31 84,3371 32 84,3357 33 84,3423 34 84,3379 35 84,3317 36 84,3505 37 84,3369 38 84,3471 39 84,3471 40 84,3396 41 84,3372 42 84,3351 43 84,3429 44 84,3374 45 84,3402 46 84,3391 47 84,3475 48 84,3373 49 84,3438 50 84,3345

Кожне окреме значення параметра, отримане у результаті і-го досліда, позначають через хі і називають варіантою, а ряд, скадений із варіант − варіаційним рядом, або рядом розподілення. Число, яке вказує скільки разів зустрічається кожна варіанта у варіаційному ряді, називається частотою.

1. Число інтервалів N вибирають в залежності від числа спостережень п згідно таблиці 1:

Таблиця 1

п N-1

40 − 100 7 − 9

100 − 500 8 − 12

500 − 1000 10 − 16

1000 − 10000 12 – 22

Число інтервалів N може бути знайдено з формули:

N=3+3,322Elgn=3,322Еlg50=9.

2. Інтервали, як правило, вибирають однакові. Довжину інтервалу визначають за формулою:

,

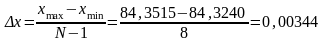При визначені границь інтервалів рекомендується починати ряд з значення, яке на 1/2 інтервала менше xmin , і закінчувати ряд значенням, яке перевищує xmax також на 1/2 інтервала. Побудову інтервального варіаційного рядка починаємо зі складання робочої таблиці, в яку заносимо інтервали, центри інтервалів і частоту варіант.

5

Знаходимо границі інтервального рядка:

ліву

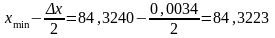(В);

праву

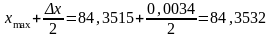(В).

Для наочності статистичне розподілення оформлюється у вигляді різних графіків, один з яких називається гістограмою. При побудові гістограми на осі абсцис відкладають інтервали, а над ними проводять відрізки, паралельні до осі абсцис з ординатами, рівними: а)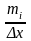 або б) .

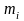У випадку а) площина і-го частинного прямокутника 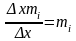− частота варіант, які входить до складу і-го варіанту. Отже, площа гістограми дорівнює сумі (об’єму вибірки) п усіх частот.

У випадку б) сума всіх ординат дорівнює об’єму вибірки п. Якщо використовується варіаційний ряд відносно частот (частостей) 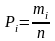, площа відповідної цьому ряду гістограми дорівнює одиниці. При побудові гістограми масштаб вибирають таким, щоб максимальна ордината складала 5/8 основи.

З даних таблиці 2 будуємо ряд розподілення (таб. 3), де mi − частота варіант у даному інтервалі.

Таблиця 3. Розподілення значень результатів вимірювання потенціометра

і	Інтервали, В	Центри інтервалів хі, В	Частоти mi
1 2 3 4 5 6 7 8 9	84,3240…84,3274 84,3274…84,3308 84,3308…84,3342 84,3342…84,3376 84,3376…84,3410 84,3410…84,3444 84,3444…84,3478 84,3478…84,3512 84,3512…84,3546	84,3257 84,3291 84,3325 84,3359 84,3393 84,3427 84,3461 84,3495 84,3529	1 3 3 15 12 9 5 1 1

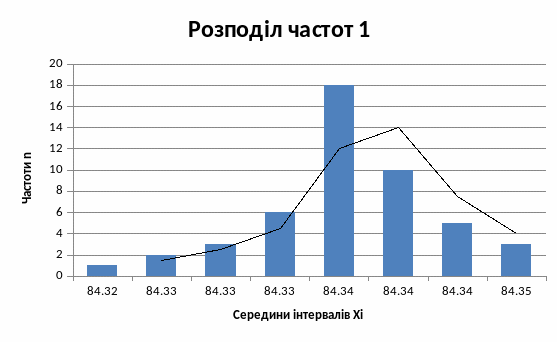
Будуємо гістограму:

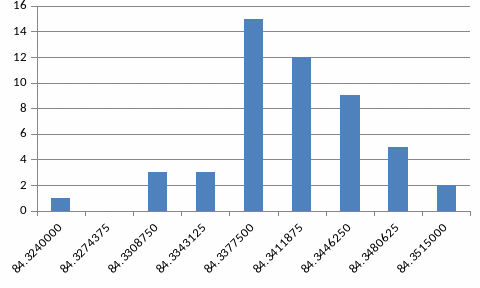
ЧИСЛОВІ ХАРАКТЕРИСТИКИ СТАТИСТИЧНОГО РОЗПОДІЛЕННЯ

В теорії ймовірностей у якості основних параметрів розподілення випадкової величини знаходять широке застосування різні числові характеристики: математичне сподівання, дисперсія, початкові і центральні моменти різних порядків. При вивчені статистичних розподілень, побудованих за вибіркованими даними, кожній числовій характеристиці випадкової величини відповідає її статистична аналогія − оцінка числової характеристики.

Ці оцінки використовуються в якості приблизних значень параметрів розподілення досліджуваної випадкової величини. Оцінки числових характеристик виражаються через вибіркові дані й з випадковості вибірок є випадковими величинами.

Для того щоб статистичні оцінки давали “гарні” наближення оці-нюваних параметрів, вони повинні бути незміщеними, ефективними і спроможними.

Незміщеною називають статистичну оцінку, математичне сподівання якої дорівнює оцінюваному параметру.

Ефективною називають статистичну оцінку, яка при п → ∞ прямує за ймовірностю до оцінюваного параметра. В математичній статиці доведено, що вимогам незміщеності, ефективності і спроможності задовольняють основні вибіркові характеристики: вибіркова середня 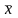і вибіркова дисперсія

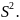
Для згрупованих даних:

,

= ;

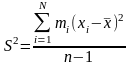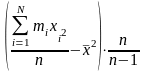Для незгрупованих даних:

,

.

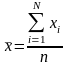Щоб спростити доволі громіздкі розрахунки, вихідні варіанти замінюють умовними:

,

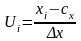де с_х − умовний нуль (новий початок відліку).

Умовні варіанти завжди являються цілими числами. Нехай в якості умовного нуля вибрана варіанта х_m . Тоді:

.

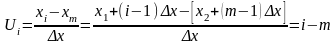Так як і та m − цілі числа, їх різниця і−m = U_i також ціле число.

Максимальна простота розрахунків досягається, якщо в якості умовного нуля вибирають варіанту, яка розташована приблизно в середині варіаційного ряду (частіше така варіанта має найбільшу частоту).

Застосування умовної варіанти дозволяє обчислювати середню вибіркову і вибіркову дисперсію S₂ за формулами:

;

,

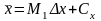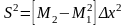де ; .

.

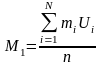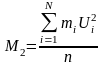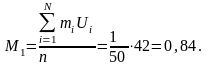
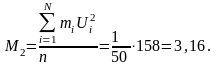
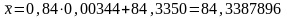При обчислені вибіркових середньої та дисперсії доцільно користуватися розрахунковою таблицею 4, яка складається:

1) перший, другий і третій стовпці утворюють статистичне розподі-лення (варіаційний ряд);

2) в четвертий стовпчик записують умовні варіанти ( в якості умовного нуля вибирають варіанту, яка розташована приблизно в середині варіаційного рядка), в клітинці рядка, яка містить умовний нуль, пишуть 0; в клітинках над нулем пишуть послідовно −1,−2,−3 і т.п., під нулем пишуть – 1; 2; 3,…;

3) добутки частоти на умовні варіанти 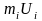записують в п’ятий стовпчик, їх суму 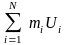розміщують у нижню клітинку стовпчика;

4) добутки частоти на квадрати умовних варіант 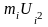записують в шостий стовпчик, їх суму розміщують в нижню клітинку стовпця;

5) добутки частоти на квадрати умовних варіантів, збільшених на одиницю 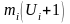записують в сьомий контрольний стовпчик, їх суму 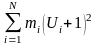розміщують в нижню клітинку стовпчика.

Сьомий стовпчик розрахункової таблиці (таб.4) слугує для контролю розрахунків: якщо сума 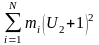буде рівною сумі (як і повинно бути у відповідності з тотожністю ), розрахунки виконані правильно.

Складаємо розрахункову таблицю 4:

Таблиця 4. Розрахунок числових характеристик

і	Інтервали, В	Центри інтервалів хі, В		Частоти mi
1 2 3 4 5 6 7 8 9	84,3240…84,3274 84,3274…84,3308 84,3308…84,3342 84,3342…84,3376 84,3376…84,3410 84,3410…84,3444 84,3444…84,3478 84,3478…84,3512 84,3512…84,3546	84,3257 84,3291 84,3325 84,3359 84,3393 84,3427 84,3461 84,3495 84,3529		1 3 3 15 12 9 5 1 1		-3 -2 -1 0 1 2 3 4 5	-3 -6 -3 0 12 18 15 4 5		9 12 3 0 12 36 45 16 25		4 3 0 15 48 81 80 25 36
Сума			50		-		42	158		292

Контроль:

; .

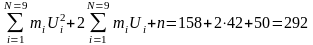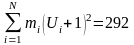Обчислення виконані правильно.

Середньоквадратичне відхилення :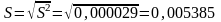 (В).

Зіставимо таблицю 5:

;

m'_i= φ(zі) ; m'̓_i – заокруглене значення.

Таблиця 5. Розрахунок теоретичних частот

№ п/п	Інтервали	Центри	mi		φ(хі)	mi′	mi''
1 2 3 4 5 6 7 8 9	84,3240…84,3274 84,3274…84,3308 84,3308…84,3342 84,3342…84,3376 84,3376…84,3410 84,3410…84,3444 84,3444…84,3478 84,3478…84,3512 84,3512…84,3546	84,3257 84,3291 84,3325 84,3359 84,3393 84,3427 84,3461 84,3495 84,3529	1 3 3 15 12 9 5 1 1	-2,43075 -1,799 -1,662 -0,5366 0,09478 0,726165 1,3575 2,0075 2,6203	0,0208 0,0790 0,2012 0,3091 0,3973 0,3056 0,1582 0,0459 0,0129	0,6643 2,5233 6,4263 10,83 12,689 9,7608 5,0529 1,466 0,412	1 3 6 11 13 10 5 1 0

11

ПЕРЕВІРКА ПРАВДОПОДІБНОСТІ СТАТИСТИЧНИХ ГІПОТЕЗ

Критерій згоди А.Н.Колмогорова

В критерії згоди А.Н.Колмогорова мірою розходження між значенням емпіричної F*(x) і теоретичної F(x) функцій розподілення є максимом модуля їх різниці:

Д_п=max|F*(x)−F(x)|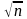

Ця величина є випадковою з законом розподілення:

F(Д_п)=Р(Д_п<α)= .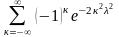

Обчислення при перемінного критерію згоди А.Н.Колмогорова зробимл за наступною методикою:

1. Знайти значення статичної функції розподілення, відповідаючи центрам х_і інтервалів варіаційного рядка.

2. Обчислити значення теоретичної функції розподілення за відповідними значеннями х_і і z_i .

3. Знайти абсолютне значення різниці між значеннями статистичної і теоретичної функції розподілення при однакових значеннях х_і , а потім вибрати найбільшу з них:

Д=max|F*(x)− F(x)|.

4. Обчислити спостережені значення критерію згоди (к_спос=λ) λ=Д _, де п − об’єм вибірки.

5. Задатися рівнем значимості α.

6. Для вибраного рівня з таблиці квантілів розподілення А.Н.Колмогорова λ₁-α визначити критичну точку λ_кр = λ₁-α .

7. Зрівняти λ₁-α з λ_кр ;

а) якщо обчислене в П.4 значення λ < λ_кр − нульова гіпотеза може рахуватись справедливою;

б) якщо λ ≥ λ₁-α − відклонити нульову гіпотезу.

Для зручності складемо таблицю 6.

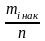емпіричної F*(x) і теоретичної F(x) функцій розподілення для центрів інтервалів х_і : F*(x_і)= ; F(xі)= .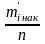

Д=max|F*(x)− F(x)|=0,04 ; λ=Д =0,04∙10=0,4; рівень значимості α = 0,05;

Таблиця 6. Перевірка гіпотези о законі розподілення за критерієм А.Н.Колмогорова

Інтервал	Центри інтервалів хі	mi	mi′'	mi нак	mi′нак	|F*(xі)−F(xі)|
84,3240…84,3274 84,3274…84,3308 84,3308…84,3342 84,3342…84,3376 84,3376…84,3410 84,3410…84,3444 84,3444…84,3478 84,3478…84,3512 84,3512…84,3546	84,3257 84,3291 84,3325 84,3359 84,3393 84,3427 84,3461 84,3495 84,3529	1 3 3 15 12 9 5 1 1	1 3 6 11 13 10 5 1 0	1 4 7 22 31 43 48 49 50	4 4 10 21 34 44 49 50 50	0 0 0,06 0,02 0 0,02 0,02 0,02 0

Д

15

ані вимірювань, приведені в таблиці 2, узгоджуються з нормальним законом розподілення цього параметра.

Критерій згоди Пірсона χ2

В критерії згоди Персона в якості міри розходження статистичного і теоретичного розподілень приймається величина χ2 (хі-квадрат):

χ2= .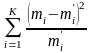

.

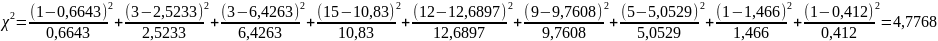Знаходимо число степенів вільності f як число інтервалів мінус число позитивних в’язей l : f = k – l=9-3=6 .Задаємося рівнем значимості α=0,05 .

Для обраного рівня і числа степенів вільності із таблиці квантілів розподілення Персона знаходтмо критичну точку χ²_кр = χ²_1-α =12,6.