Механизмы переноса тепла. Основные виды теплообмена. Теплопроводность. Температурное поле. Гипотеза Фурье.

Теплопередача, или теплообмен -это учение о самопроизвольных необратимых процессах распределения (переноса) теплоты в пространстве с неоднородным полем температуры.

Различают молекулярный и конвективный механизмы переноса теплоты.

Молекулярный перенос теплоты осуществляется посред­ством теплового движения микрочастиц в среде с неоднородным распределением температуры.

Конвективный перенос теплоты осуществляется в среде с неоднородным распределением скорости и температуры макроско­пическими элементами среды при их перемещении.

Теплопроводностью называют молекулярный перенос теплоты в сплошной среде, обусловленный наличием градиента температуры [уравнение (18.3)].

Конвективным теплообменом называют процесс, обус­ловленный совместным действием конвективного и молекулярного переноса теплоты. В инженерной практике большое значение имеет частный случай этого способа переноса теплоты, а именно: теплоотдача—конвективный теплообмен между движущейся средой и поверхностью ее раздела с другой средой: твердым телом, жидкостью или газом.

Теплообмен излучением - это процесс, который проис­ходит следующим образом: внутренняя энергия вещества превра­щается в энергию излучения (энергия фотонов или электромаг­нитных волн, излучаемых телом или средой), далее происходит распространение излучения в пространстве (процесс переноса из­лучения), далее энергия излучения поглощается веществом, кото­рое оказалось на пути фотонов или электромагнитных волн.

Процесс переноса теплоты (различными способами) от горячей жидкости к холодной через разделяющую их твердую стенку на­зывают теплопередачей.

Аналитическое исследование теплопроводности сводится к изучению пространственно-временного изменения температуры, т, е. к нахождению уравнения

(1.1)

Уравнение (1.1) представляет математическое описание температурного поля. Температурное поле есть совокупность .значений тем­пературы во всех точках изучаемого пространства для каждого момента времени.

Различают стационарное и нестационарное температурные поля. Такое поле отвечает неустановившемуся тепловому режиму теплопроводности

и носит название нестационарного температурного поля. Если тепловой режим является установившимся, то температура в каж­дой точке поля стечением времени остается неизменной и такое температур­ное поле называется стационарным.

(1.2)

Температурное поле, соответствующее уравнениям (1.1) и (1.2), является пространственным, так как температура - функция трех координат. Если температура есть функция двух координат, то поле называется двухмерным

одномерным:

Наиболее простой вид одномерного стационарного тем­пературного поля:

Количество теплоты, передаваемое через плоскую стенку, прямо пропорционально разности температур горячей Т_ω1 и холодной Т_ω2 сторон стенки, площади стенки А и времени т. и обратно пропор­ционально толщине δ стенки (рис)

(18.1)

где λ-теплопроводность вещества Вт/(м*К)

Представим (18.1) в виде

(18.2)

где q— поверхностная плотность теплового потока, Вт/м²; λ/δ— тепловая проводимость (δ/λ—термическое сопротивление).

Фурье выдвинул гипотезу, согласно ко­торой плотность теплового потока прямо про-

порциональна градиенту температуры *, т. е.

(18.3) или

где n—нормаль к изотермической поверхности; λ—теплопровод­ность, зависит от температуры в данной точке, но не зависит от градиента температуры.

Механизмы переноса тепла в движущей среде. Теплоотдача и теплопередача. Коэффициент теплоотдачи и теплопередачи. Их физичкский смысл

Теплоотдача. Рассмотрим процесс переноса теплоты от горячей жидкости с температурой Т_∞ к холодной стенке с температурой ее поверхности T_ω (рис. 18.2).

В тонком пристенном слое движущейся жидкости толщиной Δ температура уменьшается по некоторому закону T=f(y) (рис. 18,2). Слой жидкости толщиной Δ, в котором температура изменяется от температуры потока Т_м до температуры стенки T_ω, называют тепловым пограничным слоем. Вид функции T=f(y) определяется физической обстановкой в пристенном слое и в том

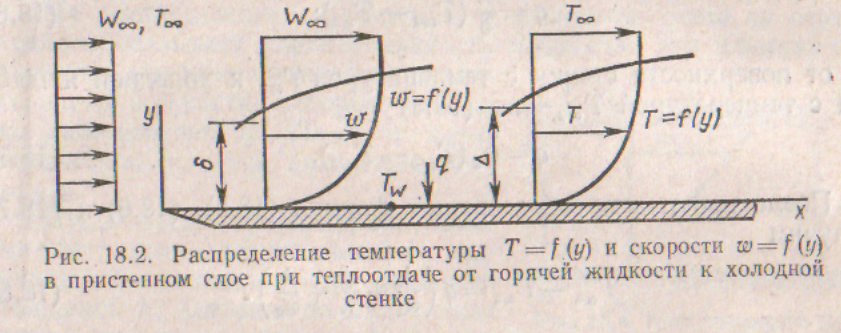
числе распределением скорости w=f(у) в этом слое жидкости. Слой жидкости толщиной 6, в котором скорость невозмущенного потока жидкости W_∞ уменьшается до нуля (w=0) на поверхности стенки, называют динамическим пограничным слоем. Эффект «прилипания» жидкости к поверхности стенки (w = 0) обу­словлен силами взаимодействия между молекулами жидкости и

твердого тела.

По толщине динамического пограничного слоя формируется распределение скорости по некоторому закону w= f(y) (рис. 18.2).

Если закон распределения температуры Т =f(у) по толщине теплового пограничного слоя установлен (теоретически или экспе­риментально), то можно определить плотность теплового потока к стенке по закону Фурье

Тепловой ноток к стенке можно определить также по закону Ньютона:

(18.4)

где Т_∞—температура жидкости за пределами теплового погранич­ного слоя; T_w—температура поверхности стенки, одинаковая во

всех ее точках.

Величину α называют коэффициентом теплообмена (теплоотдачи). Он характеризует интенсивность теплоотдачи и равен отношению плотности теплового потока q на поверхности р-зздела к температурному напору Т_∞-T_w между средой и по­верхностью.

Если выразить q в Вт/м², а температурный напор—в К, то α

выразится в Вт/(м²*К).

Теплопередача. Рассмотрим процесс переноса теплоты от горя­чей движущейся жидкости с температурой T_∞1 к холодной дви­жущейся жидкости с температурой T_∞2 через твердую стенку (рис.).

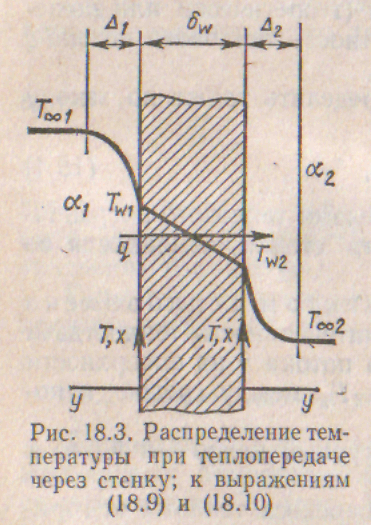
Плотность теплового потока от горячей жидкости к стенке представим в форме (18.4)

(18,5)

через стенку—по формуле (18.2)

(18,6)

от поверхности стенки с температурой T_w2 к холодной жидко­сти с температурой Т_w2-по (18.4)

(18.7)

После простых преобразований формул (18.5), (18.6) и (18.7) получим

(18.8)

Введем обозначение

где

- коэффициент теплопередачи;

Величина k имеет ту же размерность, что и α, и называется коэффициентом теплопередачи. Коэффициент теплопередачи k характеризует интен­сивность передачи теплоты от одной жидкости к другой через разделяющую их стенку и численно равен количеству теплоты, которое передается через единицу поверхности стенки в единицу времени при разности температур между жидкостями в один градус.

Уравнение энергии- Уравнение Фурье-Кирхгофа

В основе уравнения энергии лежит закон сохранения энергии. Рассмотрим элемент массы, мгновенно занимающий объем с центром в точке х, у, z (рис. 19.4, а, б).

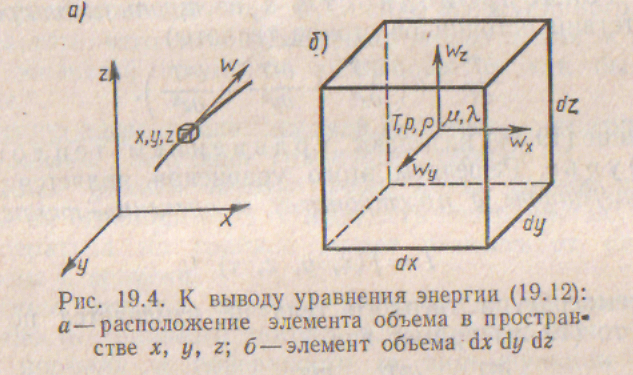
Элемент массы проходит через точку х, у, z со скоростью W. Скорость изменения температуры определяется полной производ­ной в форме

(19.10)

Скорость изменения накопленной в элементе энергии (скорость накапливания) является произведением теплоемкости с, массы ρ dx dy dz и скорости изменения температуры (19.10), т. е.

(19.11)

Скорость накапливания энергии должна быть равна скорости прихода энергии через все шесть граней элемента.

Скорость прихода энергии за счет теплопроводности опреде­ляется по закону Фурье. Плотность теплового потока в элемент в направлении оси x равна q_x =-λ∂T/∂x. Скорость прихода энергии за счет теплопроводности в направлении оси х

(19.12)

Соотношения, аналогичные (19.12), могут быть получены для скорости прихода энергии в направлении осей у и z.

Сумма трех скоростей прихода энергии по осям х, у к z уста­навливается равной скорости накапливания энергии в элементе по (19.11), т.е.

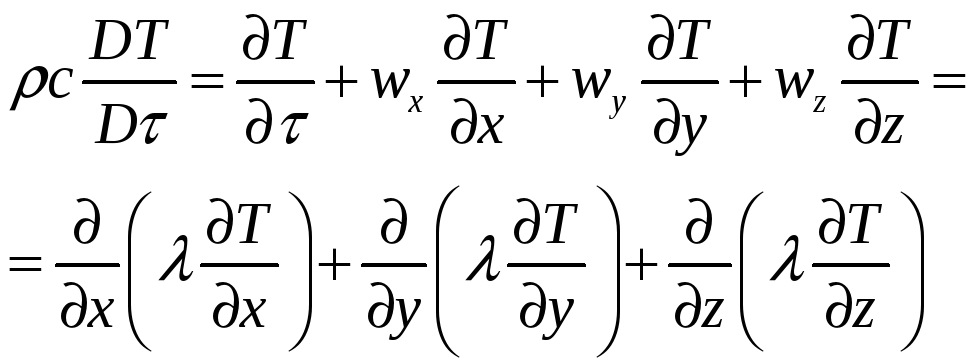(19.13)

Уравнение (19.13) называют уравнением энергии.

Динамическое уравнение движения (Навье- Стокса), его физический смысл.

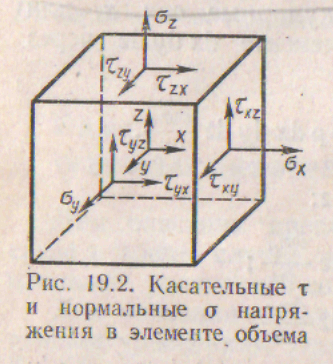
Для вывода уравнения движения используем закон сохране­ния количества движения, который гласит: изменение количества движения в элементе объема жидкости dxdydz (рис. 19.2) равно результирующей всех внешних сил приложенных к поверхности и объему элемента.

Количество движения по определению равно произведению массы выделенного элемента жидкости m = pdxdydz на скорость его движения W, Скорость—величина векторная, поток количе­ства движения mW — тоже вектор. Закон сохранения количества движения можно представить в вектор­ной форме или в форме трех скалярные уравнений для составляющих количества движения и внешних сил в направлениях х, у, z.

При выводе уравнении движения учи­тываем поверхностные силы па трех из шести граней (рис. 19.2). На каждой гра­ни для описания полной силы, действую­щей на эту грань, достаточно одного нор­мального напряжения и двух касательных напряжений.

Силы, обусловленные действием гравитации, электричества или магнетизма, представим через их состав­ляющие X, Y_t Z вдоль осей x, у, z.

Три нормальных напряжения σ_x, σ_y, σ_z. обусловлены давле­нием и" прением при растяжении элемента. Шесть касательных напряжений обусловлены степенью сдвига. Только три касатель­ных напряжения независимы. Касательные напряжения с одина­ковыми, но расположенными в обратном порядке индексами равны. Это следует из равенства моментов относительно произвольной осп при равновесии упругого тела.

Скорость изменения коли­чества движения равна массе, умноженной на скорость измене­ния w_x. Скорость может изменяться по следующим причинам:

-из-за изменения скоростного уровня всего поля потока

-из-за того, что элемент массы движется в поле переменной скорости, мгновенные градиенты которого в направлении , не равны нулю.

Уравнение движения Навье-Стокса для несжимаемой жидкости:

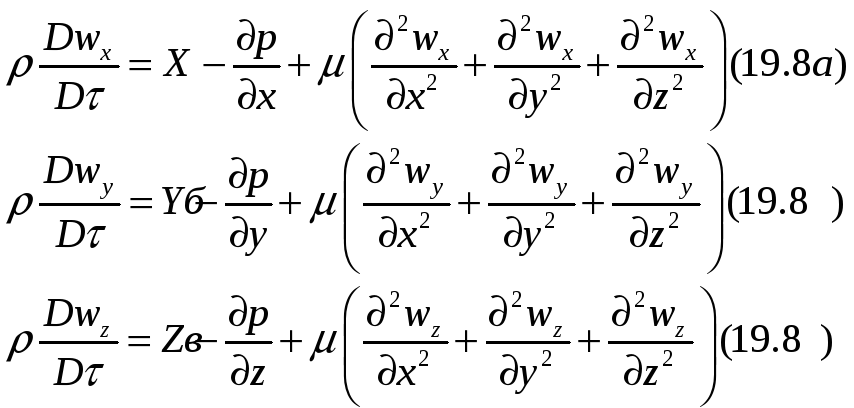
Если при изменении плотности и давления происходит изме­нение температуры (неизотермический процесс), то к системе урав­нений сплошности и движения следует присовокупить уравнение состояния в форме F(p, р,T)=0.

Для идеального газа уравнение состояния имеет вид

Все четыре члена каждого уравнения (19.8) имеют размерность силы, отнесенной к объему.

Уравнения Навье—Стокса для сжимаемых жидкостей (p=var) отличаются только нормальными напряжениями, каждое из кото­рых имеет добавочный член в уравнениях (19.7) в форме -4/3μdivW.

Уравнения определяют характер распре­деления скорости в однородном поле потока с постоянной плот­ностью. Эти уравнения применимы как к установившемуся, так и неустановившемуся течению.

Уравнение сплошности (неразрывности движения), его физический смысл

В основе этого уравнения лежит закон сохранения массы. Элемент объема жидкости (dx dydz) располагается в произвольной точке x, у, z потока (рис. 19,1, а). Состояние жидкости и свойства переноса в точке (x, у, z) обозначим через Т, р, ρ, μ,. Ско­рость потока W в координатах х, у, z выразим через ее проек­ции. w_x w_y w_z на оси х, у, z (рис. 19.1).

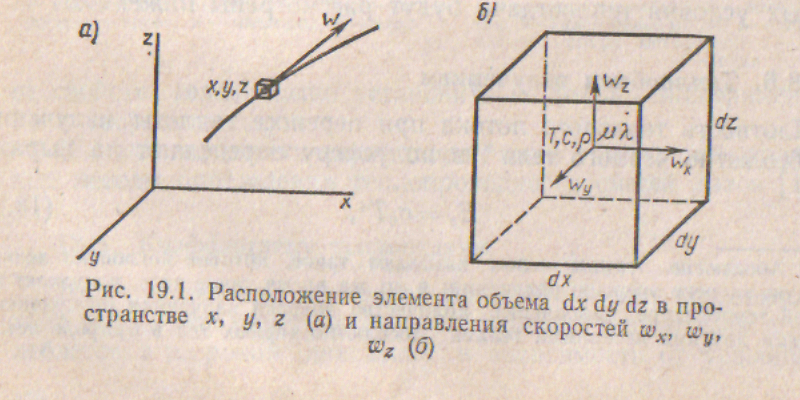
Пусть плотность жидкости постоянна р=const, тогда масса жидкости в объеме dxdydz должна сохраняться постоянной как при стационарном (скорость потока W не изменяется во времени), так и нестационарном режиме течения. Результирующий массовый расход жидкости через все шесть граней элементарного объема должен быть равен нулю.

Массовый расход жидкости вдоль осп х в точке х, у, z равен pw_x через единицу площади, а через левую грань элементарного объема (рис. 19.1,6) равен pw_xdydz. Разность массовых расхо­дов жидкости через две грани, перпендикулярные оси х, или скорость накопления (расхода) массы в элементе dxdydz через указанные грани равна

Аналогичные результаты для осей у и z:

Уравнение сплошности для потока жидкости при ρ=const полу­чим, приравнивая нулю сумму массовых расходов через все шесть граней элемента

Для потока жидкости с переменной плотностью разность между скоростью прихода массы в элемент и скоростью ухода массы из элемента равна скорости накапливания (расхода) массы элементом объема dxdydz, т. е.

Уравнение (19.2) называют уравнением сплошности. Уравнение (19.2) в векторной форме имеет вид

Вектор pW представляет собой поток массы, и его диверген­ция (div) есть скорость растекания (вытекания) на единицу объема.

Уравнение (19.2) устанавливает, что уменьшение плотности жидкости в элементе объема равно отношению скорости ее выте­кания из элемента к объему элемента.

Основное уравнение теории теплопроводности (уравнение Фурье) и его физический смысл. Краевые условия (условия однозначности). Краевые условия 1-ого, 2-ого, 3-его рода.

В основе уравнения энергии лежит закон сохранения энергии. Рассмотрим элемент массы, мгновенно занимающий объем с центром в точке х, у, z (рис. 19.4, а, б).

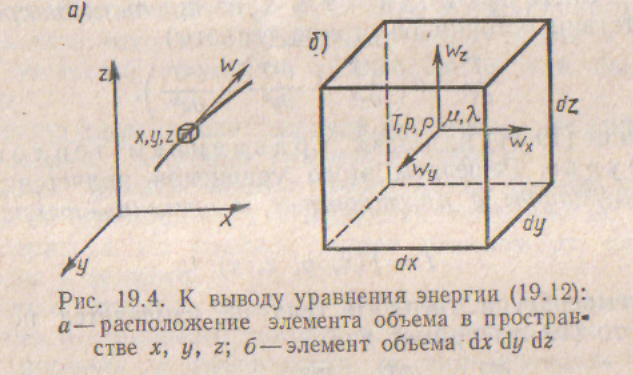
Элемент массы проходит через точку х, у, z со скоростью W. Скорость изменения температуры определяется полной производ­ной в форме

(19.10)

Скорость изменения накопленной в элементе энергии (скорость накапливания) является произведением теплоемкости с, массы ρ dx dy dz и скорости изменения температуры (19.10), т. е.

(19.11)

Скорость накапливания энергии должна быть равна скорости прихода энергии через все шесть граней элемента.

Скорость прихода энергии за счет теплопроводности опреде­ляется по закону Фурье. Плотность теплового потока в элемент в направлении оси x равна q_x =-λ∂T/∂x. Скорость прихода энергии за счет теплопроводности в направлении оси х

(19.12)

Соотношения, аналогичные (19.12), могут быть получены для скорости прихода энергии в направлении осей у и z.

Сумма трех скоростей прихода энергии по осям х, у к z уста­навливается равной скорости накапливания энергии в элементе по (19.11), т.е.

(19.13)

Уравнение (19.13) называют уравнением энергии.

Принимаем в (19.13) w_x = 0, w_y= 0_, w_z=0 а также постоян­ным коэффициент λ и, вводя обозначение а=λ/(cρ), где a — темпе­ратуропроводность (м²/с), получим уравнение нестацио­нарной теплопроводности в изотропном твердом теле (при отсутствии источников стоков теплоты)

Уравнение (19.14) называют уравнением теплопровод­ности Фурье. Решением этого уравнения является распреде­ление температуры в пространстве и времени — температурное поле

T = f(x, у, z. τ). Если температура твердого тела не изменяется по времени дТ/ди = 0 то (19.14) примет вид

где ² — оператор Лапласа; последнее уравнение называют урав­нением Лапласа.

Для исследования (расчета) конкретных процессов теплообмена нужно сформулировать и решить краевую задачу, которая должна содержать уравнения сплошности, движения и энергии плюс крае-вые условия или условия однозначности, Задать краевые условия — значит сформулировать, во-первых, начальные условия (значения искомых функций в указанных уравнениях в началь­ный момент времени т-0), во-вторых, граничные. условия на поверхностях, ограничивающих движущуюся жидкость.

Для уравнений сплошности и движения граничные условия определяются для каждой задачи, но общими для всех задач будут два следующих: первое—составляющая скорости жидкости, нормальная к поверхности твердого тела (непроницаемого), равна нулю на поверхности раздела жидкости и твердого тела; второе — при течении сплошной среды, для которой применимы указанные выше уравнения, составляющая скорости жидкости, направленная по касательной к поверхности раздела жидкости и твердого тела, также принимается равной нулю. Считается, что жидкость не скользит при соприкосновении с поверхностью, а «прилипает» к поверхности.

К уравнению энергии для искомой, функции—температуры —

1) граничные условия первого рода, когда задают значения температуры на ограничивающих жидкость поверхностях; в общем случае температура на границе может зависеть от координат точек границы и времени;

2) граничные условия второго рода, когда на поверхности задана плотность теплового потока, т, е. производная от темпе­ратуры по нормали к поверхности (в виде функции времени и координат точек поверхности);

3) граничные условия третьего рода, в которых тепловой поток предполагается пропорциональным разности температур стенки и жидкости:

в этом условии должен быть задан коэффициент теплоотдачи а, а также температура среды T_f,

через граничные условия устанавливается зависи­мость течения жидкости от формы и размеров (диаметра трубы, толщины пластины и т. д.) твердого тела, взаимодействующего с потоком.

Решение задачи опредиления темпратурного поля однослойной плоской стенки при стационарном режиме граничных условиях певого рода. Многослойная плоская стенка. Тепловой поток через однослойную и многослойную стенку

Условия задачи должны содержать уравнение теплопроводности в форме

и граничные условия, например, первого рода:

T=T₁ при x=0 (21.3a)

T=T₂ при x=δ (21.3б)

Представим (21.2) в форме

и после первого интегрирования получим

второе интегрирование дает общее решение уравнения (21.2)

где C₁ и С₂—произвольные постоянные, которые определяют, используя граничные условия (21.3).

Полагая в (21.4) х=0 и используя (21.За), получим

T₁=C₂ (21.5)

а при x=δ на основании (21.36) и (21.4) имеем

откуда

Частное решение уравнения (21.2) при граничных условиях (21.3) с учетом (21.4), (21.5) и (21.6) имеет вид

Из (21.7) видно, что Т(х) линейно зависит от x.

Плотность теплового потока q (рис. 21.1) может быть определена из закона Фурье

или в данном случае

Дифференцируя распределение температуры по толщине стенки (21,7). Получим

откуда

Из (21.8) видно, что при T₁ > T₂ плотность теплового потока положительна, т. е. поток направлен в положительном иаправлении оси х. При T₁< T₂ он будет направлен в обратную

сторону. Количество теплоты, переданное через стенку в единицу времени, вычисляется с помощью (21.8)

где А—площадь поверхности стенки, м².

Определим плотность теплового потока через трехслойную стенку (рис. 21.2); для этого вначале определим термическое сопротивление для каждого слоя (§ 18.1):

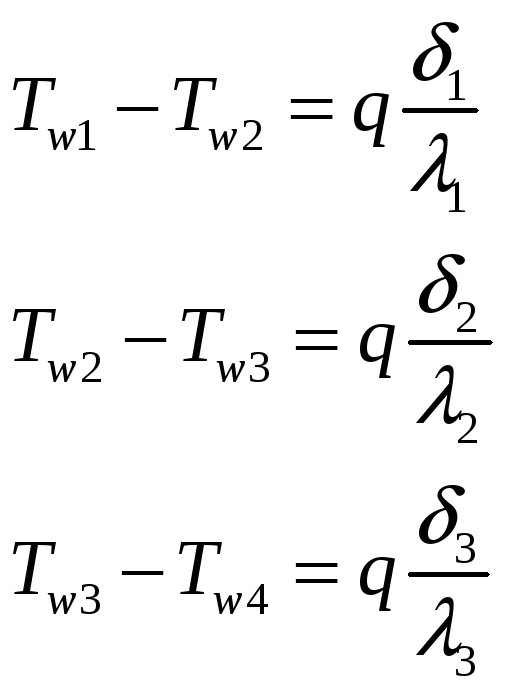
Стожим почленно полученные соотношения, в результате получим

откуда

На основании последнего соотношения для многослойной стенки , получим

Решение задачи опредиления темпратурного поля однослойной цилиндрической стенки при стационарном режиме граничных условиях певого рода. Многослойная цилиндрическая стенка. Тепловой поток через однослойную и многослойную стенку

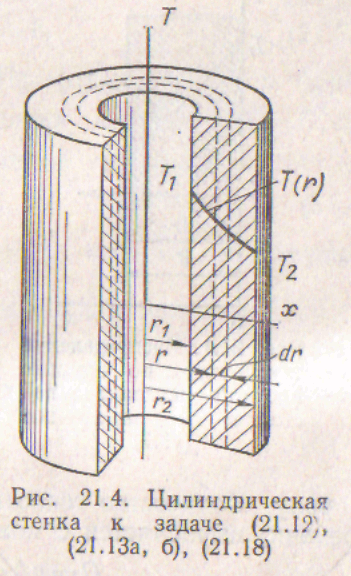
Условия задачи должны содержать уравнение теплопроводности в форме

и граничные условия, например, первого рода:

при r=r₁ T=T₁ (21.13а)

при r=r₂ T=T₂. (21.136)

Представим (21.12) в форме

и после первого интегрирования получим

откуда после второго интегрирования получим общее решение урав­нения (21,12):

Постоянные интегрирования C₁ и С₂ определим, используя (21.13) и (21.14).

Совмещая (21.13) и (21.14), получим

при r=r₁ T₁=C₁lnr₁+C₂ (21.15a)

при r=r₂ T₂=C₁lnr₂+C₂. (21.156)

Вычитая из (21.156) уравнение (21.15а), получим

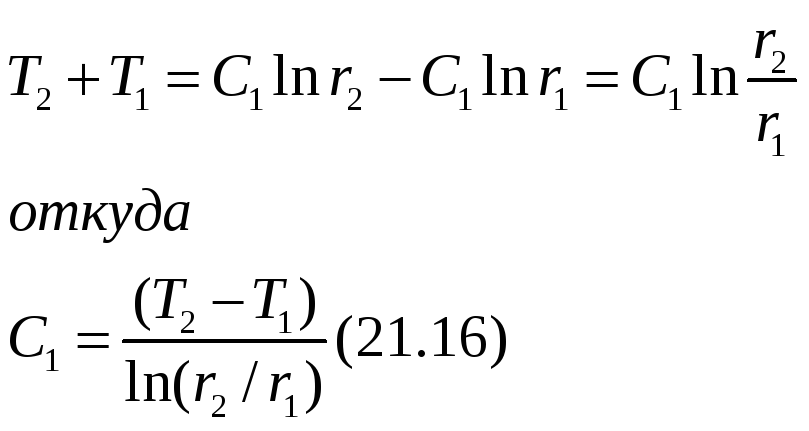
Найдем С₂ из (21.15а) и, используя (21.16), получим

Решение краевой задачи - частное решение уравнения (21.12) при граничных условиях (21.15) получим, подставляя значения С₁ (21.16) и С₂ (21.17) в общее решение (21.14)

Искомое распределение температуры по толщине цилиндрической стенки (21.18) логарифмически зависит от координаты r,

Плотность теплового потока q определяется из закона Фурье. На основании (21.18) имеем

Количество теплоты, проходящее сквозь цилиндрическую стенку, отнесенное к единице длины трубы, можно определить по формуле

Естественно, что Q не зависит от r, так как теплота нигде не аккумулируется.

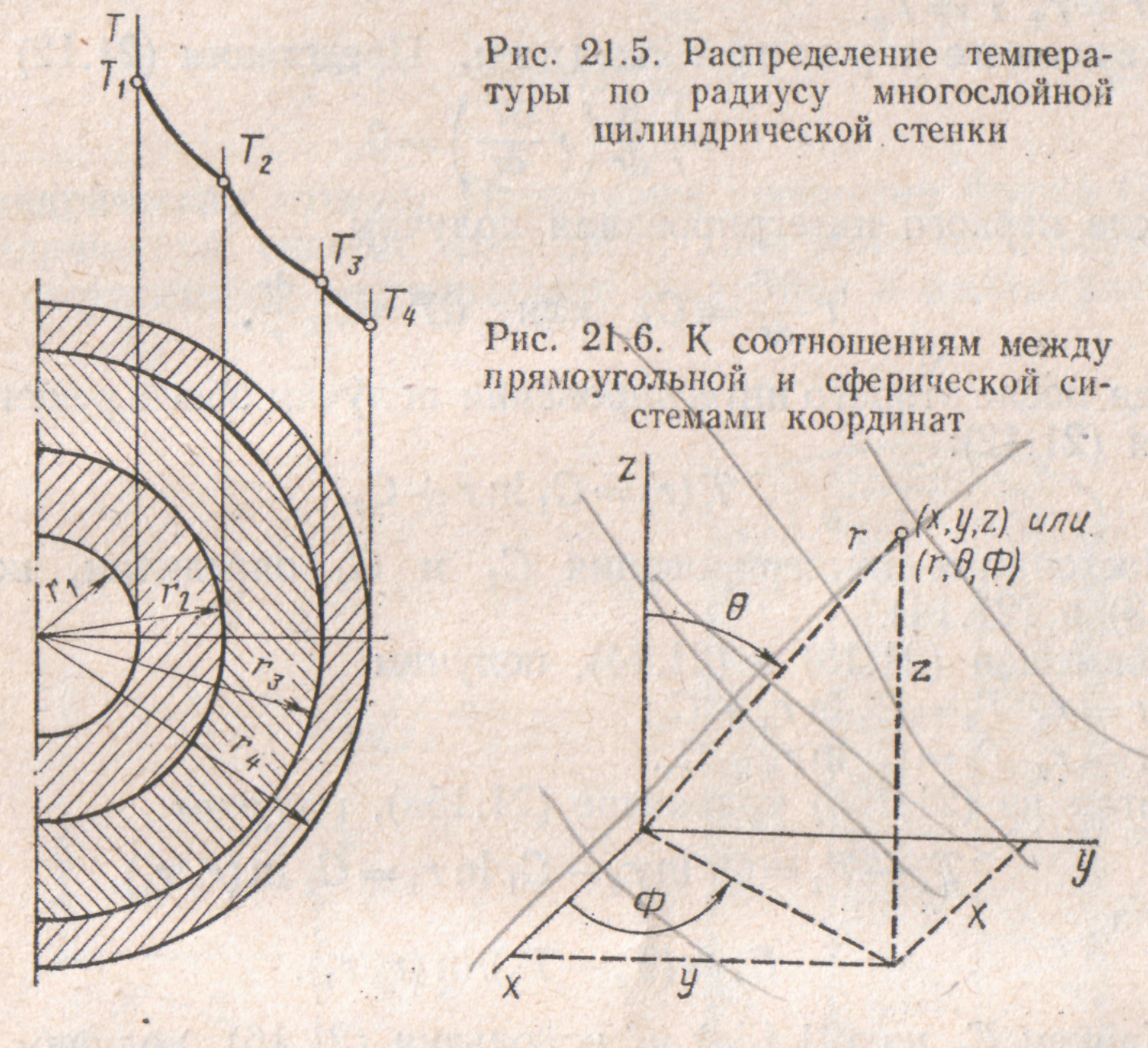
Многослойная цилиндрическая стенка. Термическое сопротив­ление многослойной цилиндрической стенки (рис. 21.5) равно сумме сопротивлений отдельных слоев. На основании этого утверж­дения и используя формулу (21.19), можно написать уравнение для определения количества теплоты, проходящего сквозь много­слойную цилиндрическую стенку:

где q_l отнесено к единице длины стенки; п—число слоев.

ПУТИ ИНТЕНСИФИКАЦИИ ТЕПЛОПЕРЕДАЧИ

Из уравнения теплопередачи

Q=kFΔt

следует, что при заданных размерах стенки и температурах жидкостей величиной, определяющей теплопередачу, является k. Но поскольку тепло­передача — явление сложное, то правильное решение можно найти только на основе анализа частных составляющих, характеризующих процесс. Так, например, если мы имеем дело с плоской стенкой, для которой

то при δ/λ→ 0 (что можно принять для тонких стенок с большим коэффи­циентом λ)

Интенсификация теплопередачи путем увеличения коэффициентов тепло­отдачи. Из уравнения (2.77) следует, что значение коэффициента тепло­передачи не может быть больше самого малого значения α. При α₂→∞k' стремится к своему предельному значению α₁. При а₁ →∞ коэффициент теплопередачи стремится к α₂.

Из рассмотренного примера видно, что при α_а<< α₂ увеличение большего из коэффициентов теплопередачи (α₂) практически не дает увеличения k. Увеличение меньшего из коэффициен­тов теплоотдачи (α₁) в 2 и 5 раз дает увеличение k' почти во столько же раз. На рис. 2.11 приведена зависимость k' = f (α₁, α₂) согласно формуле (2.77). Из графика следует, что при увеличе­нии а_х значение k' быстро растет до тех пор, пока α₁ не сравняется с α₂. После того как α₁ станет больше α₂, рост k' замедляется и при дальнейшем увеличении α₁ практически прекра­щается. Следовательно, при α₁<<а₂ для увеличения k' следует увеличивать a_l ,т. е. уменьшать большее из термических сопротивлений 1/а_г. Иначе говоря, при а₁ << а₂ увеличение k' возможно только за счет увеличения а₁. Если α₁≈α₂, увеличение коэффициента теплопередачи возможно за счет увеличения любого из α.

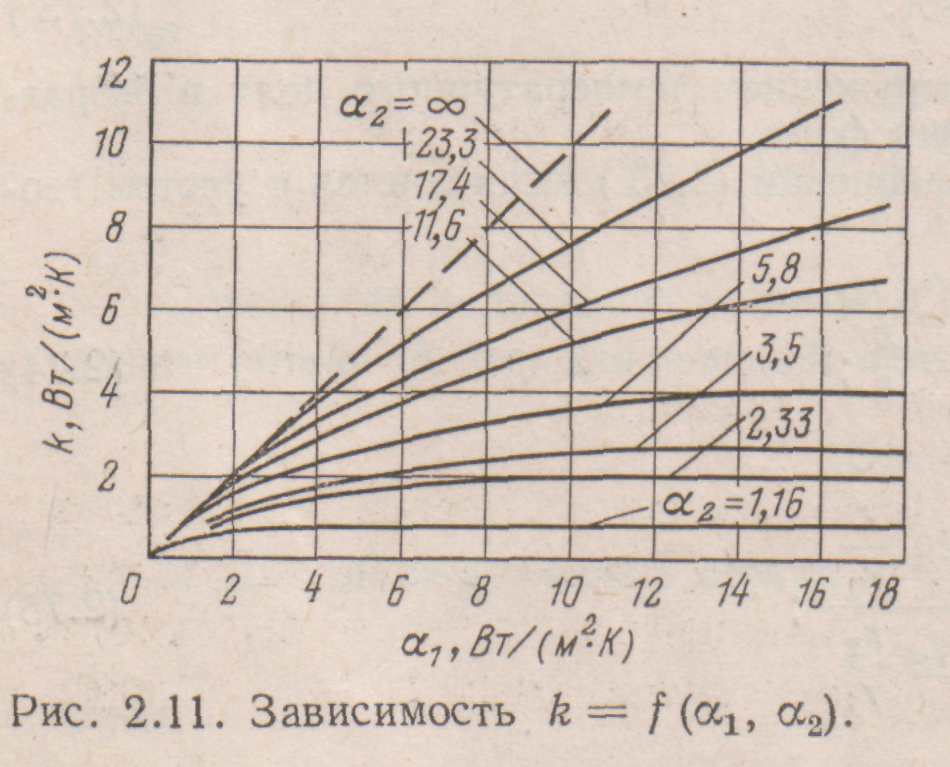
Интенсификация теплопередачи за счет оребрения стенок. При передаче теплоты через цилиндрическую стенку термические сопротивления l/α₁d₁ и l/α₂d₂ определяются не только значениями коэффициентов теплоотдачи,

размерами самих поверхностей. При передаче теплоты через шаровую стенку влияние диаметров d₁ и d₂ оказывается еще сильнее, что видно из соотношений l/α₁d²₁ и l/α₂d²₂. Отсюда следует, что если значение а мало, то термическое сопротивление теплоотдачи можно уменьшить путем увеличе­ния соответствующей поверхности. Такой же результат можно получить и для плоской стенки, если одну из площадей поверхности увеличить путем оребрения. Последнее обстоятельство и положено в основу интенсификации теплопередачи за счет оребрения. При этом термические сопротивления станут пропорциональными величинам

Следует указать, что при использовании метода оребрения нужно руко­водствоваться следующими соображениями: если α₁ <<a₂ то оребрять по­верхность со стороны α₁ следует до тех пор, пока α₁F₁, не достигает значения α₂F₂. Дальнейшее увеличение площади поверхности F₁, малоэффективно. Ребристые поверхности изготавливаются или в виде сплошных отливок, или отдельных ребер, прикрепленных к поверхности.

Строгое аналитическое решение задачи о распространении теплоты в ребре связано со значительными трудностями. В основу решения поэтому кладут некоторые допущения, которые позволяют сравнительно простым путем получить нужный результат. Ниже рассмотрим метод решения задач о теплопроводности в ребрах простейших геометрических форм.

Теплопередача через однослойную и многослойную цилиндрическую стенку при стационарном режиме. Анализ полного термического сопротивления теплопередачи цилиндрической стенки.

Граничные условия третьего рода (теплопередача). Рассмотрим одно­родную цилиндрическую стенку (трубу) с постоянным коэффициентом тепло­проводности λ. Заданы постоянные температуры подвижных сред t_Ж1 и t_Ж2 и постоянные значения коэффициентов теплоотдачи на внутренней и наруж­ной поверхностях трубы а₁ и а₂ (рис. 2.7).

Необходимо найти q_l и t_c. Будем полагать, что длина трубы велика по сравнению с толщиной стенки. Тогда потерями теплоты с торцов трубы можно пренебречь, и при установившемся тепловом режиме будет проходить через стенку и отдаваться от стенки к холодной жидкости одно и то же коли­чество теплоты.

Обозначим:

С учетом (2.50) уравнение (2.49) запишется в виде

Величина k_l называется линейным коэффициентом теплопередачи и измеряется в Вт/(м-К). Она характеризует интенсивность передачи теплоты от одной среды к другой через разделяющую их стенку. Значение k_l численно равно количеству теплоты, которое проходит через стенку длиной 1 м в единицу времени от одной среды к другой при разности температур между ними 1 К.

Величина R_l = l/k_l м-К/Вт, обратная линейному коэффициенту тепло­передачи, называется линейным термическим сопротивлением теплопере­дачи. Она равна:

где 1 /α₁d₁ и 1/α₂d₂ — термические сопротивления теплоотдачи на соответ­ствующих поверхностях, обозначим их соответственно R_l1 и R_l2;

1/2λInd₂/d₁— термическое сопротивление теплопроводности стенки, обозначим его через

R_lc

При теплопередаче через многослойную цилиндрическую стенку система равенств (2.48') должна быть заменена системой, учитывающей сопротивление теплопроводности всех слоев:

После сложения равенств и решения относительно q_l Вт/м, полу­чим:

Величина

называется полным термическим сопротивлением многослойной цилиндри­ческой стенки и измеряется в м-К/Вт.

Из уравнения следует, что

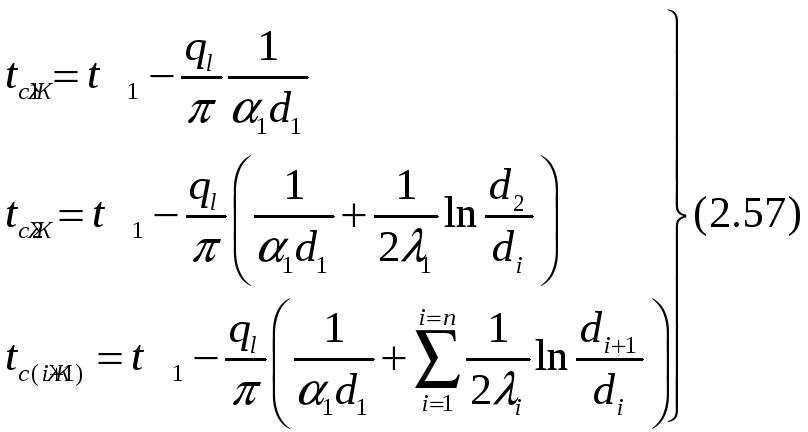
При задании граничных условий первого рода их можно рассматривать как предельный случай граничных условий третьего рода, когда коэффи­циенты теплоотдачи на поверхностях α₁ и α₂ устремляются к бесконечности, в силу чего t_Ж1 и t_Ж2 становятся равными t_c1 и t_c(n+1) При этих условиях уравнение (2.56) принимает вид:

Теплопередача через однослойную и многослойную плоскую стенку при стационарном режиме.

Величина, обратная коэффициенту теплопередачи, называется полным термическим сопротивлением теплопередачи:

Из (2.25) видно, что полное термическое сопротивление складывается из частных термических сопротивлений 1/α₁ δ/λ и 1/α₂, причем 1/α₁ =R₁ -термическое сопротивление теплоотдачи от горячей жидкости к поверхности стенки; δ/λ = R_с — термическое сопротивление теплопроводности стенки; 1/α₂ = R₂ — термическое сопротивление теплоотдачи от поверхности стенки к холодной жидкости.

Поскольку общее термическое сопротивление состоит из частных терми­ческих сопротивлений, то совершенно очевидно, что для многослойной стенки нужно учитывать термическое сопротивление каждого слоя. Если стенка состоит из п слоев, то полное термическое сопротивление теплопере­дачи через такую стенку будет равно:

отсюда

Плотность теплового потока через многослойную стенку, состоящую из п слоев, будет равна:

Уравнение (2.27) для многослойной стенки подобно уравнению (2.24) для однородной плоской стенки. Различие заключается в выражениях для коэффициентов теплопередачи k. При сравнении уравнений (2.26) и (2.23) видно, что соотношение (2.23) является частным случаем уравнения (2.26), когда п =1

Тепловой поток Q, Вт, через поверхность F твердой стенки равен:

Q = qF = kΔtF.(2.28)

Температуры поверхностей однородной стенки

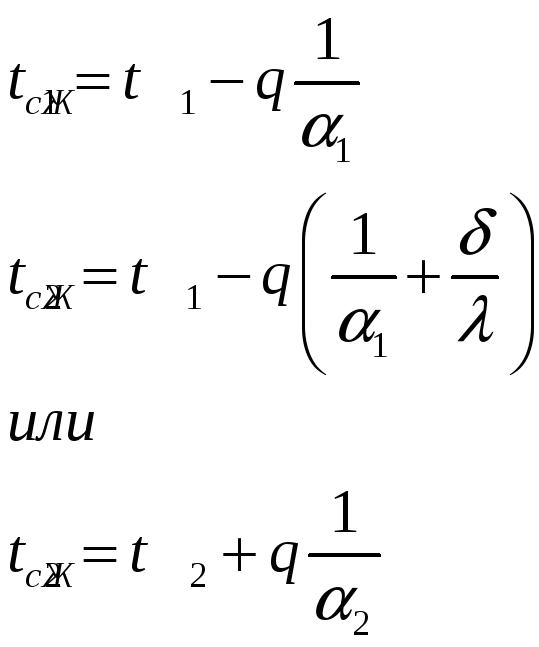
На основании сказанного температура на границе любых двух слоев i и i +1 при граничных условиях третьего рода может быть определена по уравнению

Критический диаметр изоляции. «Ложная изоляция»

Рассмотрим влияние изменения наружного диаметра на термическое сопротивление однородной цилиндрической стенки

При постоянных значениях α₁, d₁, λ и α₂ полное термическое сопротивле­ние теплопередачи цилиндрической стенки будет зависеть от внешнего диаметра. Из уравнения (2.51) следует, что при этих условиях 1/α₁d₁≡R_l1 = const.

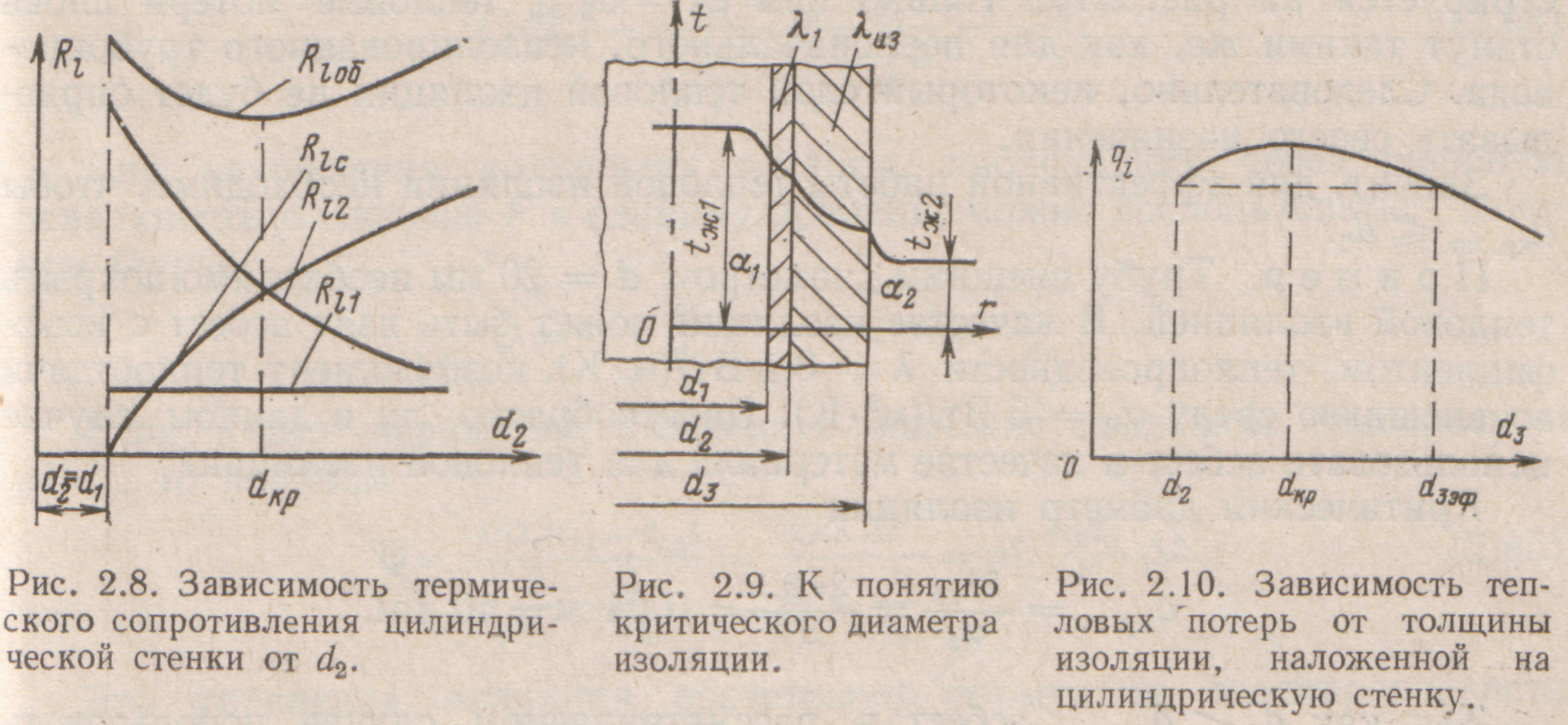
Термическое сопротивление теплопроводности 1/2λIn d₂/d₁≡R_lc с увели­чением d₂ будет возрастать, а термическое сопротивление теплоотдачи l/α₂d₂ =R_l2 будет уменьшаться. Очевидно, что полное термическое сопро­тивление будет определяться характером изменения составляющих R_lc и R_l2. Изменение частных термических сопротивлений изображено на рис. 2.8.

Чтобы выяснить, как будет изменяться R_l при изменении толщины ци­линдрической стенки, исследуем R_l как функцию d₂. Возьмем производную от r_l по d₂ и приравняем нулю:

Значение d₂ из последнего выражения соответствует экстремальной точке кривой R_l = / (d₂). Исследовав кривую любым из известных способов на максимум и минимум, увидим, что в экстремальной точке имеет место минимум. Таким образом, при значении диаметра d₂= 2λ/α₂ термическое сопротивление теплопередачи будет минимальным.

Значение внешнего диаметра трубы, соответствующего минимальному полному термическому сопротивлению теплопередачи, называется крити­ческим диаметром и обозначается d_Kp. Рассчитывается он по формуле

При d₂<d_кр с увеличением d₂ полное термическое сопротивление тепло­передачи снижается, так как увеличение наружной поверхности оказывает на термическое сопротивление большее влияние, чем увеличение толщины :тенки.

При d₂>d_кр с увеличением d₂ термическое сопротивление теплопере­дачи возрастает, что указывает на доминирующее влияние толщины стенки.

Изложенные соображения необходимо учитывать при выборе тепловой изоляции для покрытия различных цилиндрических аппаратов и трубо­проводов.

Рассмотрим критический диаметр изоляции, наложенный на трубу (рис. 2.9). Термическое сопротивление теплопередачи для такой трубы

Из уравнения q_l=πΔt/R_l следует, что q_l при увеличении внешнего диаметра изоляции d₃ сначала будет возрастать и при d₃ = d_Kp будет иметь максимум q_l. При дальнейшем увеличении внешнего диаметра изоляции q_l будет снижаться (рис. 2.10).

Выбрав какой-либо теплоизоляционный материал для покрытия цилин­дрической поверхности, прежде всего нужно рассчитать критический диаметр по формуле (2.60) для заданных λ_из и α₂.

Если окажется, что значение d_Kp больше наружного диаметра трубы d₂, то применение выбранного материала в качестве тепловой изоляции нецеле­сообразно. В области d₂<d₃<d_{Kp из} при увеличении толщины изоляции будет наблюдаться увеличение теплопотерь. Это положение наглядно иллю­стрируется на рис. 2.10. Только при d₃=d_3эф тепловые потери вновь станут такими же, как для первоначального, неизолированного трубопро­вода. Следовательно, некоторый слой тепловой изоляции не будет оправ­дывать своего назначения.

Значит, для эффективной работы тепловой изоляции необходимо, чтобы

d_кр.из≤d₂

Метод обобщенных переменных. Представление о подобии физических явлений. Условия необходимые и достаточные.

Для того чтобы_придать результатам численного или экспери­ментального решения обобщенный характер, т. е. сделать решение пригодным не только для одного конкретного явления, но и для группы подобных явлений и для уменьшения числа параметров задачи, применяют метод обобщенных переменных. Этим и ограничиваются возможности названного метода.

Содержание метода обобщенных переменных состоит в замене отдельных параметров задачи, представленных первоначальными величинами, комплексами, составленными из нескольких первона­чальных величин, заданных по условию.

Теплопроводность. Доказано [19], что решение задачи о тепло­проводности в твердом теле для нестационарного периодического процесса при заданных значениях чисел Фурье и Био и распре­деления относительных переменных величин (если необходимо) в начальный момент и на границах тела можно найти в форме следующей однозначной зависимости:

где υ/υ₀—искомая переменная—температура твердого тела в от­носительной форме; τ/τ₀, х/l, у/1, z/l — независимые переменные — время и координаты в относительной форме. Величины υ₀, τ₀, l₀ задаются по условию задачи; следует подчеркнуть, что при реше­нии задачи об определении температурного поля твердого тела коэффициент теплоотдачи во всех случаях — величина заданная. Покажем, что решение (20.10) имеет обобщенный характер. Существует бесчисленное количество первоначальных величин а = λ/(cρ), τ₀, l, которые при объединении в число Фурье дадут одно и то же число. Все это справедливо и для числа Био. Но каждый набор из первоначальных величин а = λ/(cρ), τ₀, l, соот­ветствует конкретному единичному случаю. Следовательно, реше­ние в форме (20.10) остается справедливым для бесчисленного количества единичных случаев, у которых как число Фурье, так и число Био одинаковы. Значит, решение (20.10) имеет обобщенный характер, а все единичные случаи, оля которых это решение оказывается справедливым, родственны .между собой. Это объяс­няется тем, что соотношения между основными физическими эф­фектами во всех случаях одинаковы, так как для них одинаковы числа Фурье и Био, а краевые условия подобны между собой. Явления, между которыми наблюдается такое соответствие, физически подобны.

Группа единичных случаев, у которых числа (например, Фурье и Био) одинаковы, составляет обобщенный индивидуаль­ный случай. Единичные случаи, составляющие обобщенный индивидуальный случай, подобны между собой.

Конкретные значения чисел подобия (и если необходимо—от­носительное распределение переменных величин в начальный мо­мент и на границах системы), присоединенные к соответствующим дифференциальным уравнениям, описывающим класс явлений (например, явления теплопроводности в твердом теле), выделяют из него (класса) обобщенный индивидуальный случай и, следова­тельно, могут рассматриваться как обобщенная форма краевых условий.

Следовательно, количественным признаком подобия является одинаковость чисел (например, Фурье и Био), составленных только из заданных параметров математического описания процесса, по этому их называют числами подобия.

Заключение о равенстве чисел подобия для подобных между cобой процессов теплопроводности, описанных тождественными уравнениями, остается справедливым для любых явлений тепло­обмена.

Итак, необходимым и достаточным условием подобия двух или более процессов теплообмена является равенство в них одноимен­ных чисел подобия

Понятие о пограничном слое. Диф. Уравнения динамического ламинарного пограничного слоя.

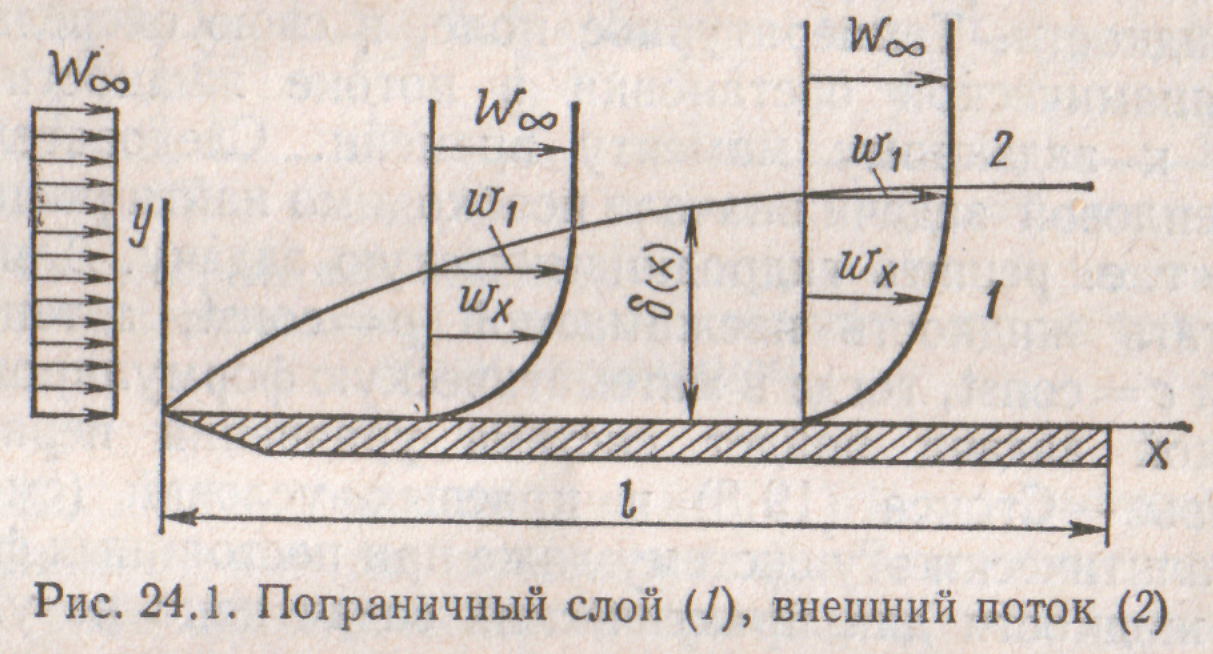
Пограничным слоем называют область течения вязкой теплопро водной жидкости, характеризующуюся малой толщиной δ(х) го сравнению с продольными размерами области, например длиной пластины l (δ(x)<<l) (рис. 24.1), и большим поперечным градиен­том, например скорости dw_x/dy или температуры, изменением

которых обусловлен процесс переноса соответственно количества движения и теплоты. Пограничный слой, характеризующийся большим поперечным градиентом продольной составляющей ско­рости dw_x/dy, под действием которого осуществляется поперечный перенос количества движения, называют динамическим.

Для динамического пограничного слоя, который представляет собой весьма малую по размерам пространственную область, удается значительно упростить уравнения Навье—Стокса (19.8). Получен­ные после упрощения уравнения называют уравнениями динами­ческого пограничного слоя.

Опуская процедуру упрощении , приведем здесь систему уравнений динамического пограничного слоя (24.2а,б) и сплошности (24.2в), которая получена для случая больших чисел

Рейнольдса в форме

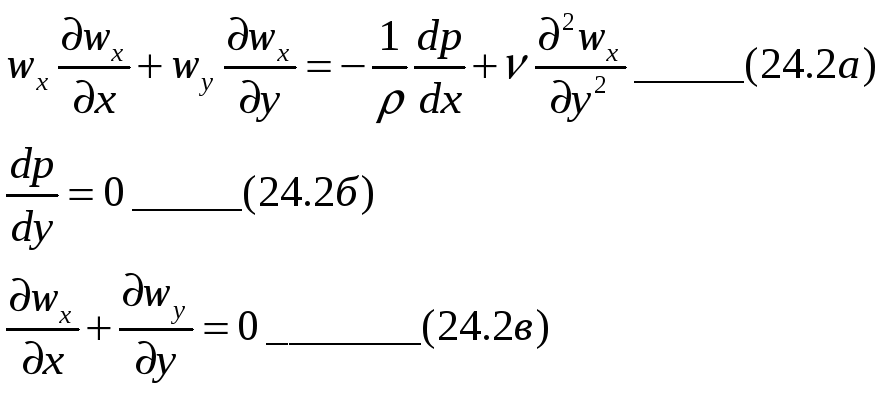
при следующих граничных условиях:

1) при y = 0 w_x=w_y =0

2) при у→∞ w_x=W_∞ где W_∞ — скорость внешнего потока вдоль оси y.

Первое из граничных условий не вызывает сомнений, так как, по условию «прилипания» к стенке при y=0 продольная

составляющая скорости w_x равна нулю; рассматривается непроницаемая стенка, поэтому поперечная составляющая скорости w_y у поверхности стенки также равна нулю. Смысл второго условия состоит в следующем: как уже отмечалось, переход w_x к W_∞ осуществляется асимптотически при y→∞. Однако при решении (24.2) с заданной точностью допускают, что w_x — W_∞ при y = δ(х) (рис. 24.1).

Второй и третий члены в правой части (24.1а) имеют одина­ковую физическую природу. Сравним их по величине. Втором член зависит от изменения скорости w_x вдоль оси х; третий — от изменения скорости w_x по оси у. Изменением скорости w_x по оси х можно пренебречь, так как рассматривается течение вдоль тела малой кривизны. Изменение скорости w_x по оси у происхо­дит от w_x= 0 на стенке до W∞ за пределами пограничного слоя, т. е. скорость w_x изменяется значительно. Поэтому второй член существенно меньше третьего, и он не включен в (24.2а). В процессе упрощения (24.1) показано, что

Отметим, что кроме системы уравнений (24.2) и граничных условий (1) и (2) должен быть задан профиль продольной ско­рости w_x в некотором начальном сечении потока, например, при

x=x₀, т. е. должна быть задана зависимость w_x.=f(x₀ y) Решение системы (24.2) и граничных условий сводится к определеннию профилей скорости в пограничном слое при х≠х₀.

Впервые система уравнений (24.2) и граничных условий была точно решена Г. Блазиусом для течения вдоль пластины. Однако даже в этом простом случае решение оказалось громоздким.

Получено точное решение системы уравнений пограничного соя еще для нескольких частных случаев при взаимодействии с ми простой формы. Однако наибольший интерес представляет общий случай — взаимодействие потока жидкости с телом заданной формы. Именно такие задачи встречаются в инженерной практике. Для них разработаны приближенные методы решения уравнений пограничного слоя.

10. Метод обобщенных переменных. Обобщенные переменные и обобщенное уравнение для теплоотдачи. Физический смысл чисел Rе, Еu, Рr, Gа, Аr, Gr, Ре, Рr, Nu.

ОТВЕТ:

1.      Подобие граничных условий (подобие процессов теплопереноса на границе между стенкой и потоком жидкости) характеризуется критерием Нуссельта:

Nu является мерой соотношения толщины пограничного слоя и определяющего геометрического размера (для трубы – её диаметр d).

2. Условие подобия в ядре потока выражает критерий Фурье (равенство критериев Фурье в сходственных точках тепловых потоков - необходимое условие подобия неустановившихся процессов теплообмена):

3. Критерий Фурье является аналогом критерия гомохронности Ho при гидродинамическом подобии (учитывает неустановившийся характер движения в подобных потоках).

4. Критерий Пекле является мерой соотношения между теплом, переносимым путём конвекции и путём конвекции и путём теплопроводности при конвективном теплообмене:

5. Критерий Рейнольдса отражает влияние силы трения на движение жидкости (характеризует отношение инерционных сил к силам трения в подобных потоках):

6. Критерий Фруда отражает влияние силы тяжести, или собственного веса, на движение жидкости (является мерой отношения силы инерции к силе тяжести в подобных потоках):

Необходимыми условиями подобия процессов переноса тепла является соблюдение гидродинамического (характеризуется равенством критериев Ho, Re, Fr в сходственных точках подобных потоков)и геометрического подобия (характеризуется постоянством отношения основных геометрических размеров стенки L1, L2, …Ln к некоторому характерному размеру L0 = d – обычно диаметру трубы).

Таким образом, обобщённое (критериальное) уравнение конвективного теплообмена выражается функцией вида:

или с учётом того, что критерий Нуссельта является определяемым, так как в него входит искомая величина коэффициента теплоотдачи:

7.

где - критерий Прандтля (характеризует подобие физических свойств теплоносителей в процессах конвективного теплообмена) является мерой подобия полей температур и скоростей).

Значения критерия Прандтля для капельных жидкостей порядка 3 – 300 и значительно уменьшаются с возрастанием температуры, а для газов постоянны и зависят от атомности газа (Pr ~ 0.7 – 1). Поэтому для жидкостей тепловой подслой тоньше гидродинамического.

С введением критерия Pr обобщённое уравнение конвективного теплообмена принимает вид

При установившемся процессе теплообмена из обобщённого уравнения исключаются критерии Fo и Ho. При вынужденном движении, когда влияние сил тяжести на гидродинамику потока, отдающего или воспринимающего тепло, пренебрежимо мало, влиянием критерия Fr на теплоотдачу можно пренебречь. Тогда:

вид этой функции определяется опытным путём, причём обычно ей придают степенную форму. Так, например, при движении потока в трубе диаметром d и длиной l может быть представлено в виде:

где С, m, n, p – величины, определяемые из опыта.

8. До сих пор обсуждались задачи с вынужденным движением жидкости. Рассмотрим, например, процесс нагревания воды в кастрюле. В этом случае нельзя исключить из уравнения критерий Фруда, т.к. сила тяжести служит причиной воздействия естественной конвекции. Однако для расчёта критерия Fr необходимо знать скорость движения конвективных токов жидкости, определить которую весьма сложно. Попробуем исключить скорость, комбинируя критерии Fr и Re:

Полученный безразмерный комплекс величин называют производным критерием Галилея:

9. Умножив критерий Ga на безразмерную разность плотностей нагретой и холодной жидкости, являющуюся причиной естественной конвекции, получим критерий Архимеда:

10. Т.к. изменение плотности при нагревании связано с коэффициентом объёмного расширения , можем заменить разность плотностей разностью температур:

подставив это выражение в критерий Архимеда, получим критерий для характеристики теплоотдачи в условиях естественной конвекции – критерий Грасгофа (мера отношения сил трения к подъёмной силе, определяемой разностью плотностей в различных точках неизотермического потока):

Следовательно, для процессов теплоотдачи при естественной конвекции, или свободном движении жидкости, обобщённое уравнение теплоотдачи имеет вид:

Для газов Pr~1=const и, значит, критерий Pr можно исключить из обобщённых уравнений для определения

18. Теплоотдача при ламинарном течении жидкости в трубах. Вязкостный вязкостногравитационный режимы течения. Структура обобщенных уравнений. Учет зависимости физических свойств жидкости от температуры. Учет влияния свободной конвекции.

ОТВЕТ:

Теплоотдача при ламинарном движении жидкости в трубах.

Ламинарный режим течения наблюдается при малых скоростях потока и малых диаметрах канала.

Турбулентный режим течения наблюдается при больших скоростях потока и больших диаметрах канала.

Скорость перехода потока от ламинарного режима к турбулентному называется критической и определяется соотношением скорости течения и диаметра трубы.

Для ламинарного режима характерно параболическое распределение скорости течения

Перенос тепла от одного слоя жидкости к другому по нормали к стенке в основном осуществляется теплопроводностью, в тоже время каждый слой жидкости имеет различную скорость движения вдоль оси, при этом теплота вдоль потока передается конвекцией. В следствии этого теплообмен при ламинарном режиме сильно зависит от гидродинамической картины течения.

Зададимся следующими условиями: пусть на входе в трубу температура жидкости t_f постоянна и отличается от температуры стенки t_w, по мере движения потока т-ра жидкости меняется и образуется пограничный слой. На некотором расстоянии от начала трубы тепловые пограничные слои смыкаются и в теплообмене участвует весь поток

На практике л.р.т. встречается у очень сильно вязких жидкостей (нефть, масло), в которых число Pr значительно выше 1. в этом случае длина начального участка довольно большая, и при Re 200-500 длина такого участка может достигать 5000 d трубы. При этом в пределах начального теплового участка т-рный градиент в жидкости убывает т .к. температурный напор уменьшается, но центральная часть потока в теплообмене не участвует,=> локальный коэффициент теплоотдачи по длине начального участка уменьшается до того момента как пограничные слои сольются, дальше к-т теплоотдачи принимает некоторое постоянное среднее значение.