
- •1.Способы задания движения точки. Системы отсчета
- •2. Перемещение. Скорость равномерного прямолинейного движения.
- •3. Уравнение равномерного прямолинейного движения точки, его графическое представление
- •5. Ускорение.
- •6. Движение с постоянным ускорением. Единица ускорения.
- •7. Скорость при движении с постоянным ускорением
1.Способы задания движения точки. Системы отсчета
Задать движение точки означает задать ее положение в каждый момент времени. Положение это должно определяться, в какой-либо системе координат. Однако для этого не обязательно всегда задавать сами координаты; можно использовать величины, так или иначе с ними связанные. Ниже описаны три основных способа задания движения точки.
1. Естественный способ. Траекторией называется совокупность точек пространства, через которые проходит движущаяся материальная частица. Это линия, которую она вычерчивает в пространстве. При естественном способе необходимо задать :
а) траекторию движения (относительно какой-либо системы координат);
б) произвольную точку на ней нуль, от которого отсчитывают расстояние S до движущейся частицы вдоль траектории;
в) положительное направление отсчета S ;
г) начало отсчета времени t;
д) функцию S(t), которая называется законом движения**) точки.
2. Координатный способ. Это наиболее универсальный и исчерпывающий способ описания движения. Он предполагает задание:
а) системы координат (не обязательно декартовой) q1, q2, q3;
б) начало отсчета времени t;
в) закона движения точки, т.е. функций q1(t), q2(t), q3(t).
Говоря о координатах точки, мы всегда будем иметь ввиду ее декартовы координаты.
3. Векторный способ. Положение точки в пространстве может быть определено также и радиус-вектором, проведенным из некоторого начала в данную точку. В этом случае для описания движения необходимо задать:
а) начало отсчета радиус-вектора r;
б) начало отсчета времени t;
в) закон движения точки r(t).
2. Перемещение. Скорость равномерного прямолинейного движения.
![]()
![]()
Равномерное
движение — механическое движение, при
котором тело за любые равные отрезки
времени проходит равные перемещения.
Равномерное движение материальной
точки — это движение, при котором
скорость точки остаётся неизменной.
Перемещение, пройденное точкой за время,
задаётся в этом случае формулой.
![]()
Прямолинейное равномерное движение — это движение, при котором тело (точка) за любые равные и бесконечно малые промежутки времени проходит одинаковые перемещения. Вектор скорости точки остаётся неизменным, а её перемещение есть произведение вектора скорости на время:
Скорость показывает, какое перемещение совершает тело за единицу времени, двигаясь прямолинейно и равномерно.
Например, если модуль скорости равна 5 м/с, это значит, что за каждую секунду своего движения тело, двигаясь прямолинейно и равномерно, перемещается на 5 м.
3. Уравнение равномерного прямолинейного движения точки, его графическое представление
Скорость равномерного прямолинейного движения - это постоянная векторная величина, равная отношению перемещения тела за любой промежуток времени к значению этого промежутка.
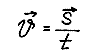 (векторная
форма записи формулы скорости)
(векторная
форма записи формулы скорости)
Перемещение.![]()
Расчетные
формулы: проекция вектора перемещения
и проекция вектора скорости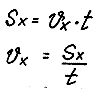
Уравнение
прямолинейного равномерного движения:
![]()
Графики прямолинейного равномерного движения.
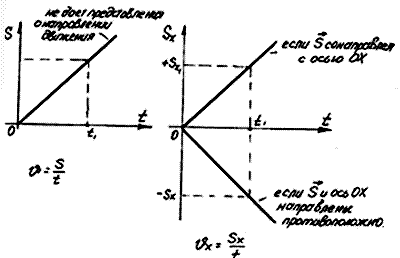
Уравнение движения, то есть зависимость координаты тела от времени х = х(t), принимает вид:
х = x0 + vt Если положительное направление оси ОХ противоположно направлению движения тела, то проекция скорости тела на ось ОХ отрицательна, скорость меньше нуля (v < 0), и тогда уравнение движения принимает вид:
х = x0 – vt
4. Мгновенная скорость. Сложение скоростей.
Мгновенная и средняя скорость
Полезно отличать понятие средней скорости перемещения от понятия средней скорости пути, равной отношению пройденного точкой пути ко времени, за которое этот путь был пройден. В отличие от скорости перемещения, средняя скорость пути — скаляр.
Когда говорят о средней скорости , для различения, скорость согласно выше приведённому определению называют мгновенной скоростью. Так, хотя мгновенная скорость бегуна, кружащего по стадиону, в каждый момент времени отлична от нуля, его средняя скорость (перемещения) от старта до финиша оказывается равной нулю, если точки старта и финиша совпадают. Заметим, что при этом, средняя путевая скорость остаётся отличной от нуля.
В
классической механике абсолютная
скорость точки равна векторной сумме
её относительной и переносной скоростей:
![]()
Простым языком: Скорость движения тела относительно неподвижной системы отсчёта равна векторной сумме скорости этого тела относительно подвижной системы отсчета и скорости самой подвижной системы отсчета относительно неподвижной системы.
